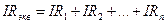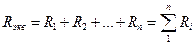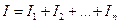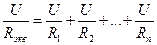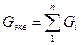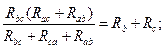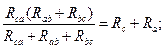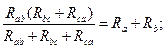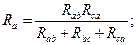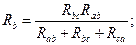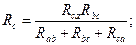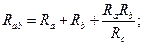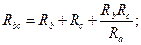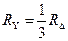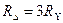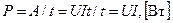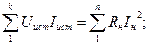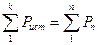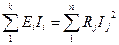Что значит схема замещения

Лекция №2. 1. Схемы замещения электрических цепей

1. Схемы замещения электрических цепей

2. Эквивалентные преобразования пассивных электрических цепей

3. Расчет цепей посредством двух законов Кирхгофа

4. Мощность в цепях постоянного тока

5. Баланс мощностей

1. Схемы замещения электрических цепей

Схемой электрической цепи называется ее графическое изображение с использованием обозначений идеальных элементов. Например:

Если учесть сопротивление утечки реального конденсатора, сопротивление витков реальной индуктивной катушки и внутреннее сопротивление реального источника ЭДС, то можно составить соответствующие схемы замещения этих элементов:

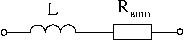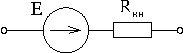Отсюда следует, что все схемы по сути дела являются лишь более или менее точными схемами замещения реальных электрических цепей.

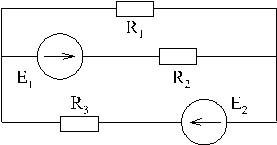
Представленный на рис.2 контур содержит три участка: участок с постоянным напряжением U = Е, не зависящим от тока источника, и участки с напряжениями RвхI и U на нагрузке Rн.

Направление ЭДС выбрано совпадающим с направлением тока, но оно противоположно напряжению на этом элементе.

Для определения параметров схемы замещения источника электрической энергии с линейной внешней характеристикой нужно провести два опыта — холостого хода (I=0; U=Uх=Е) и короткого замыкания (I=Iк; U=Е-RвнI).

2. Эквивалентные преобразования пассивных электрических цепей

Для упрощения анализа сложных электрических цепей отдельные их участки, не содержащие ЭДС, или пассивные цепи целиком можно заменить одним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в остальной части цепи.

При последовательном соединении сопротивлений по каждому из них

протекает один тот же ток, следовательно, падение напряжения на эквивалентном сопротивлении должно быть равно сумме падений напряжений на исходных сопротивлениях:

Если группа заменяемых сопротивлений соединена параллельно, то

напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопротивление будет равен сумме токов через отдельные параллельные сопротивления:

Используя закон Ома для отдельного сопротивления, можем записать:

Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости 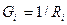, получим:

При анализе сложных схем встречаются случаи, когда часть схемы образует так называемый треугольник сопротивлений:

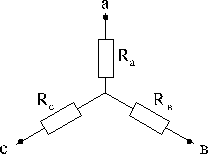Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса заменить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наоборот, необходимо обратное преобразование звезды в треугольник. Схемы треугольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразованиями) остаются неизменными.

Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам «а», «в», «с». Например, при обрыве провода, подходящего к узлу «а», сопротивления между точками «в» и «с» в треугольнике и звезде должны быть одинаковы, т.е.:

Рассуждая аналогичным образом, можно записать:

Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:

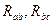
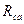
Решая систему относительно и получим формулы преобразования звезды в треугольник:

В частном случае, когда сопротивления звезды или треугольника одинаковы, эти формулы упрощаются:

3. Расчет цепей посредством двух законов Кирхгофа

а) произвольно задаются положительными направлениями токов во всех ветвях схемы,

б) для всех узлов схемы кроме одного составляются уравнения по 1-му закону Кирхгофа,

в) для всех независимых контуров составляются уравнения по 2-му закону Кирхгофа (контур будет считаться независимым от остальных, если в него входит хотя бы одна новая ветвь, т.е. не вошедшая в состав других контуров).

Общее число уравнений, составленных по 1 и 2-му законам Кирхгофа должно быть равно числу неизвестных токов. Полученная система линейных уравнений разрешается относительно токов с использованием известных методов решения систем уравнений (например, с помощью определителей)

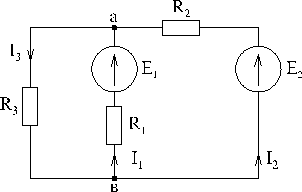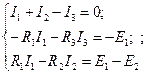Если при решении системы уравнений значение какого-либо тока получилось отрицательным, то это означает, что истинное направление тока противоположно выбранному. Данный метод расчета является универсальным, однако расчет вручную возможен лишь для несложных схем (4-5 неизвестных тока). Для более сложных схем требуется применение иных методов или вычислительной техники.

4. Мощность в цепях постоянного тока

Для оценки энергетических условий важно знать сколь быстро совершается работа.

Отношение работы «А» к соответствующему промежутку времени t определяет мощность:

Используя закон Ома, можно получить другие формулы для мощности в электрических цепях:

5. Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс — баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком «-» если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Схема замещения и её параметры

Каждый элемент схемы электропередачи в общем случае можно представить П- или Т-образной схемой замещения. Линии электропередачи обычно представляют П-образной схемой замещения (приложение Д). Чтобы определить параметры схемы замещения линии, необходимо знать её удельные (погонные) параметры – активные (r₀, Ом/км) и индуктивные (х₀, Ом/км) сопро­тивления, активную (g₀, См/км) и емкостную (b₀, См/км) проводимость, длину ( 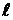, км)и число цепей и др.

Удельные активные и индуктивные сопротивления проводов ВЛ можно опреде­лить по приложению З или из другой справочной литературы. В соответствии с правилами устройства электроустановок [3] при проекти­ровании линий электропередачи стремятся к тому, чтобы потери энергии на корону в них были малы, при этом потери из-за токов утечки по изо­ляторам совсем незначительны. Это позволяет при расчетах линий на­пряжением 110 кВ активную проводимость в схемах замещения считать равной нулю. Удельную емкостную проводимость ВЛ 110 кВ можно определить по приложению З.

Умножив удельные параметры линии на её длину ( 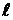, км), можно опреде­лить соответствующие параметры схемы замещения:

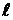
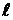
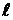
R=r₀× ; X=x₀× ; B=b₀× . (4.1)

Зарядные мощности (Мвар) участков ЛЭП в курсовой работе допускается определять по но­минальному напряжению U_ном (кВ) линии, т.е.

(4.2)

где В – емкостная проводимость линии, См.

Трансформаторы для расчетов линий 110 кВ и выше обычно заме­няют Г-образной схемой замещения.

Параметры схемы замещения трансформаторов определяют, зная каталожные данные трансформаторов (коэффициент трансформации k_Т, потери холостого хода ΔР_х и короткого замыкания ΔР_к, ток холостого хода I_х), которые могут быть найдены по данным государственных стан­дартов на конкретные трансформаторы или по справочным материалам, например, по приложению Ж или из [2].

Активное сопротивление схемы замещения двухобмоточного трансформатора R_Т (Ом), приведенное к номинальному напряжению U_ном (кВ), стороны ВН (высшего напряжения):

(4.3)

где ΔР_к – потери короткого замыкания, кВт;

U_ном – высшее номинальное напряжение, кВ;

S_ном – номинальная мощность трансформатора, МВА.

Индуктивное сопротивление Х_Т (Ом):

(4.4)

где u_к – напряжение короткого замыкания, %;

U_ном, S_ном – то же, что и для формулы (4.3).

Активные сопротивления R_1Т, R_2Т и R_3Т лучей звезды в схеме заме­щения трехобмоточного трансформатора (приложение Д) находят по общему активному сопротивлению трансформатора (4.3).

При соотношении мощностей обмоток 100/100/100% (соответствует заданию в курсовой работе):

(4.5)

где размерность величин та же, что для формулы (4.3).

(4.6)

(4.7)

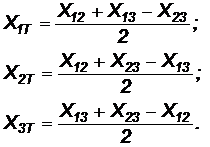
где u_к(1-2), u_к(1-3) и u_к(2-3) – каталожные значения напряжений короткого замыкания, %, для соответствующих пар обмоток; размерность остальных величин та же, что для формул (4.3), (4.4).

Передача электроэнергии по сети сопровождается потерями мощности в линиях и в трансформаторах. Потери мощности в линии электропередачи ΔS (МВА) определяются по следующим выражениям:

(4.8)

(4.9)

где P и Q – мощности в конце расчетного участка линии, МВт и Мвар;

R и X – сопротивления расчетного участка линии, Ом;

U_ном – номинальное напряжение, кВ.

Потери мощности ΔS_Т (МВА) в «n» параллельно работающих двухобмо­точных трансформаторах определяют по формулам:

(4.10)

(4.11)

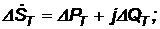
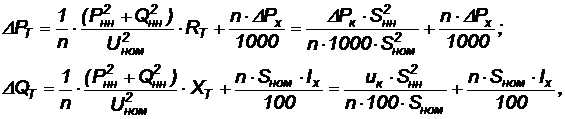
где S_нн = Р_нн + j Q_нн – нагрузка трансформатора, МВА;

S_ном – номинальная мощность трансформатора, МВА;

ΔР_к и ΔР_х – потери мощности короткого замыкания и холостого хода трансформатора, кВт;

u_к – напряжение короткого замыкания, %;

I_х – ток холостого хода трансформатора, %.

Потери мощности ΔS_Т (МВА) в «n» параллельно работающих трехобмоточных трансформаторах находят по формуле (4.10) и по выражениям, аналогичным (4.11):

(4.12)

При соотношении мощностей обмоток 100/100/100% потери ΔР_к (кВт), соответствующие лучам схемы замещения, определяются по каталожным значениям потерь короткого замыкания для пар обмоток:

Если в справочных данных указано только значение ΔР_{к вн-нн}, то потери ко­роткого замыкания всех обмоток одинаковы и равны 0,5 ΔР_{к вн-нн}.

Аналогично по каталожным значениям напряжений короткого замыкания (%) для пар обмоток u_к(13), u_к(12), u_к(23) определяются напряжения короткого замыкания для лучей схемы замещения:

В формулах (4.12) нагрузка обмотки ВН трансформатора:

(4.15)

Схему замещения электрической сети в целом составляют по схе­мам замещения её элементов с учетом их соединения и режима работы сети (см. приложение Д). Следует учесть, что в минимальном режиме работы сети нагрузка всех под­станций уменьшается в четыре раза, а все остальные параметры можно принять неизменными.

Расчетные схемы

Для составления расчетной схемы сети все заданные нагрузки подстанций на сторонах низшего (Ś_нн) и среднего (Ś_сн) напряжения при­водят к стороне расчетного (высшего) напряжения.

Нагрузка понизительной подстанции, приведенная к стороне ВН, слагается из суммы заданных нагрузок (Ś_нн) и (Ś_сн) и потерь в сопротив­лениях и проводимостях трансформаторов ΔŚ_Т, то есть

Расчетная нагрузка представляет собой сумму приведенной на­грузки и половин зарядных мощностей линий (W1, W2), присоединенных к шинам ВН данной подстанции:

(4.17)

Благодаря использованию расчетных нагрузок подстанций упро­щается расчетная схема, так как она освобождается от трансформато­ров (см. приложение Д).

Если в задании подстанция №3 подключена к кольцевой сети через ВЛ 110 кВ (схемы а, в, г, д), то расчетную нагрузку этой подстанции, приведенную к данному узлу кольцевой сети, определяют с учетом потерь мощности в линии 110 кВ.

Источник