Что значит сгруппировать слагаемые

Группировка слагаемых и множителей, правило, примеры.

К суммам трех и большего количества слагаемых относится тождественное преобразование, имеющее название группировка слагаемых. Аналогичный вид преобразований существует и для произведений трех, четырех и т.д. множителей, называемый группировкой множителей. В этой статье мы разберем правила группировки слагаемых и множителей, и рассмотрим применение этих правил на примерах.

Навигация по странице.

Группировка слагаемых, примеры

В числовых и буквенных выражениях, содержащих суммы трех и большего количества слагаемых, можно выполнять группировку слагаемых. Что же понимают под этим термином?

Под группировкой слагаемых подразумевается совместное рассмотрение нескольких слагаемых в сумме. Иными словами, группировка слагаемых – это объединение слагаемых в группу.

Существует правило группировки слагаемых: сначала в исходной сумме выполняется перестановка слагаемых так, чтобы группируемые слагаемые оказались рядом, после чего они заключаются в скобки.

Прежде чем перейти к рассмотрению примеров, поясним, на чем основано приведенное правило группировки слагаемых. Оно базируется на переместительном и сочетательном свойстве сложения.

Переходим к примерам. Рассмотрим сумму трех слагаемых вида 1+2+3 . Пусть мы хотим выполнить группировку первого и второго слагаемых. В этом случае нам не нужно выполнять перестановку слагаемых, так как слагаемые, которые мы собираемся сгруппировать, итак находятся рядом. Нам нужно лишь заключить их в скобки, имеем (1+2)+3 . На этом группировка слагаемых завершена.

Разберем еще один пример. Возьмем числовое выражение 1+8+2+9 , представляющее собой сумму четырех слагаемых, и сгруппируем первое слагаемое с последним, а второе – с третьим. Для этого сначала переставляем слагаемые так, чтобы те слагаемые, которые мы собираемся сгруппировать, оказались рядом: 1+9+8+2 . Осталось заключить группируемые слагаемые в скобки (1+9)+(8+2) .

По озвученному правилу выполняется и группировка слагаемых в выражениях с переменными. Например, в сумме вида x+y 3 +3·y 2 +2·x 2 +y+1 можно сгруппировать все слагаемые с переменной x и все слагаемые с переменной y , после этого преобразования мы получим выражение (x+2·x 2 )+(y 3 +3·y 2 +y)+1 .

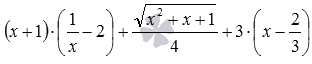
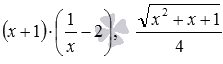
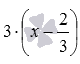
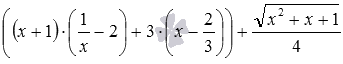
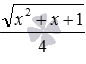
Следует заметить, что часто основные трудности с группировкой слагаемых заключаются не в самой группировке, а в том, чтобы разглядеть в исходном выражении сумму и составляющие ее слагаемые. Особенно это касается громоздких выражений. Когда слагаемые найдены, их группировка не вызывает проблем. Например, выражение представляет собой сумму трех слагаемых и . После того, как мы определили эти слагаемые, мы можем сгруппировать, например, первое слагаемое с третьим, при этом получим выражение . Кстати, в дроби под знаком корня находится сумма трех слагаемых, в которой тоже можно провести группировку.

Группировка слагаемых широко применяется для рационального вычисления значений выражений, при упрощении выражений и при решении многих других математических задач. К примеру, при вычислении значения выражения 1/3+2/7+2/3+3/7 удобно сгруппировать дроби с одинаковым знаменателем, что упрощает и ускоряет вычисления: 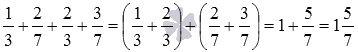. К слову, на группировке слагаемых базируется один из методов разложения многочлена на множители.

Группировка множителей, примеры

Группировка множителей по своему смыслу аналогична группировке слагаемых, только она проводится не в суммах, а в произведениях. Так под группировкой множителей в произведении понимают объединение нескольких множителей в группу.

Группировка множителей проводится по правилу, которое также аналогично правилу группировки слагаемых: группируемые множители переставляются в произведении так, чтобы они оказались рядом одно за другим, после чего они заключаются в скобки. Теоретической базой этого правила являются переместительное и сочетательное свойство умножения.

Для примера сгруппируем отдельно числовые и отдельно буквенные множители в произведении 3·a·7·b . Для этого сначала выполняем перестановку множителей, чтобы группируемые множители оказались рядом, имеем 3·7·a·b , после чего записываем скобки. В результате группировки множителей приходим к выражению вида (3·7)·(a·b) .

Источник

Способ группировки

Способ группировке в алгебре — один из способов разложения многочлена на множители.

Способ группировки можно разбить на два этапа:

1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).

2) Вынесение полученного общего для всех групп множителя за скобки.

Группируем первое слагаемое со вторым, третье — с четвертым.

Лучше при группировке между скобками всегда ставить знак «+»:

Из первых скобок выносим общий множитель a, из вторых — -3. При вынесении «-» за скобки все знаки в скобках меняем на противоположные:

Общий множитель (x+7) выносим за скобки:

Группировать можно было иначе: первое слагаемое — с третьим, второе — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — 7:

Общий множитель (a-3) выносим за скобки:

При любом способе группировки ответ получается одинаковый (от перестановки мест множителей произведение не меняется).

Группируем первое слагаемое со вторым, третье — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — «-«:

Общий множитель (4-y) выносим за скобки:

Внимание! Сколько слагаемых было до вынесения общего множителя за скобки, ровно столько же должно остаться после вынесения. Если общий множитель совпадает с одним из слагаемых (с точностью до знака), на месте этого слагаемого после вынесения общего множителя за скобки остается единица (+1 или -1).

Сгруппируем первое слагаемое со вторым и третьим, четвертое — с пятым и шестым:

Из первых скобок выносим общий множитель a, из вторых — -b:

Общий множитель (a²+1+b²) выносим за скобки:

Можно было группировать и по два слагаемых. Например, первое — с четвертым, второе — с пятым, третье — с шестым:

Из первых скобок выносим общий множитель a², во вторых скобках общего множителя нет, из третьих — b²:

Общий множитель (a-b) выносим за скобки. Не забываем поставить единицу на место (a-b)!

Источник

Группировка слагаемых

Группировка слагаемых — это объединение слагаемых в группы с помощью скобок. При группировке слагаемых обычно изменяется порядок их следования в сумме для удобства вычислений.

Метод группировки слагаемых можно применять к суммам, состоящим из трёх и более слагаемых. Группировку можно разбить на три последовательных действия:

1. нахождение слагаемых, которые можно объединить в группу;
2. перестановка слагаемых (применение переместительного закона сложения);
3. заключение слагаемых в скобки (применение сочетательного закона сложения).

Рассмотрим нахождение значения выражения, изображённого на картинке:

Можно просто сначала сложить первые два слагаемых, к полученной сумме прибавить третье слагаемое, а к полученному результату затем прибавить четвёртое слагаемое:

15 + 27 + 55 + 13 = 42 + 55 + 13 = 97 + 13 = 110,

но в данном случае значение выражения будет легче найти, если сначала сгруппировать слагаемые так, чтобы в сумме они давали круглые числа:

15 + 27 + 55 + 13 = (15 + 55) + (27 + 13) = 70 + 40 = 110.

Приём группировки слагаемых обычно используется для упрощения вычислений.

Пример. Вычислить значение выражений, используя приём группировки слагаемых.

1) 248 + 123 + 52 + 7;

2) 101 + 67 + 19 + 3;

3) 340 + 114 + 60 + 26;

4) 154 + 235 + 13 + 115 + 46.

1) 248 + 123 + 52 + 7 = ( 248 + 52) + ( 123 + 7) = 300 + 130 = 430;

2) 101 + 67 + 19 + 3 = ( 101 + 19) + ( 67 + 3) = 120 + 70 = 190;

3) 340 + 114 + 60 + 26 = ( 340 + 60) + ( 114 + 26) = 400 + 140 = 540;

4) 154 + 235 + 13 + 115 + 46 = ( 154 + 46) + ( 235 + 115) + 13 = 200 + 350 + 13 = 563.

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник