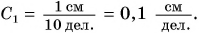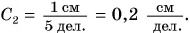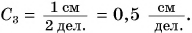Что значит с точностью до метра

Предложения со словосочетанием «с точностью до метра»

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова митохондрия (существительное):

Ассоциации к слову «точность&raquo

Ассоциации к слову «метр&raquo

Синонимы к словосочетанию «с точностью до метра&raquo

Сочетаемость слова «точность&raquo

Сочетаемость слова «метр&raquo

Значение слова «точность&raquo

ТО́ЧНОСТЬ , -и, ж. 1. Свойство по прил. точный (в 1, 2, 3 и 4 знач.). Точность веса. Точность стрельбы. Точность формулировки. (Малый академический словарь, МАС)

Значение слова «метр&raquo

МЕТР 1 , -а, м. 1. Мера длины в метрической системе мер, равная ста сантиметрам, принятая за основную единицу длины в Международной системе единиц.

МЕТР 2 , -а, м. 1. Лит. Определенное повторяющееся соотношение ударных и безударных слогов внутри стихотворной строки; стихотворный размер.

МЕТР 3 , -а, м. Устар. Учитель, наставник. (Малый академический словарь, МАС)

Источник

Reach: GPS с точностью до сантиметра

Современные технологии спутниковой навигации обеспечивают определение местоположения с точностью порядка 10-15 метров. В большинстве случаев этого достаточно, однако, в некоторых случаях требуется большее: скажем, автономный дрон, достаточно быстро перемещающийся над земной поверхностью, будет чувствовать себя неуютно в облаке из координат с метровыми погрешностями.

Для уточнения спутниковых данных используются дифференциальные системы и RTK (real-time kinematics) технологии, но до последнего времени подобного рода устройства были дорогими и громоздкими. Последние достижения цифровой техники в лице микрокомпьютера Intel Edison помогли решить эту проблему. Итак, встречайте: Reach – первый компактный высокоточный приемник GPS, очень доступный по цене, и, к тому же, разработанный в России.

Для начала поговорим немного о дифференциальных технологиях, которые позволяют Reach добиться столь высоких результатов. Они хорошо известны и достаточно широко внедрены. Дифференциальные навигационные системы (ДНСС) улучшают точность определения местоположения и скорости подвижных пользователей за счет предоставления данных измерений или корректирующей информации от одной или нескольких базовых станций.

Координаты каждой базовой станции известны с высокой точностью, так что данные измерений станцией служат для калибровки данных расположенных рядом приемников. Приемник может вычислить теоретическое расстояние и время распространения сигнала между собой и каждым спутником. Когда эти теоретические значения сравниваются с данными наблюдений, то различия представляют собой ошибки в принимаемых сигналах. Корректирующая информация (данные RTCM) получается из этих различий.

Точность определения координат с помощью Reach. Обратите внимание на масштаб.

Корректирующая информация может получаться устройством Reach из двух источников. Во-первых от общедоступной сети базовых станций через интернет по протоколу NTRIP (Networked Transport of RTCM via Internet Protocol), реализующего идею, описанную выше, применительно к глобальной компьютерной сети. Во-вторых, с помощью второго Reach, занимающего стационарную позицию вблизи первого и являющегося, таким образом, базовой станцией в терминах ДНСС. Второй вариант предпочтительнее (точность ДНСС сильно падает с увеличением расстояния между приемником и БС) – не случайно в рамках краудфайндинговой кампании на сайте Indiegogo создатели Reach первой позицией предлагают выкупить именно набор из двух устройств.

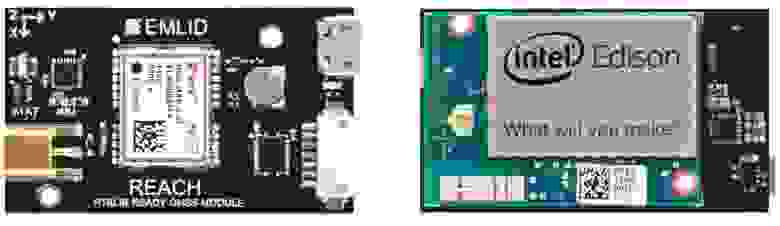
Спецификации устройства приведены в таблице ниже. Как видим, аппаратно он состоит из 3 частей: компьютера Intel Edison, на котором запущена ОС Linux и RTK софт RTKLIB; GPS-приемника U-blox NEO-M8T и антенны Tallysman TW4721. Обратите внимание, что приемник поддерживает все существующие спутниковые системы: GPS, ГЛОНАСС, Beidou и QZSS. Вся эта совокупность программных и аппаратных компонент обеспечивает впечатляющую точность определения координат: до 2 см!

Спутниковый приемник	U-blox NEO-M8T — 72 channels, output rate up to 18Hz, supports GPS/QZSS L1 C/A, GLONASS L10F, BeiDou B1, SBAS L1 C/A: WAAS, EGNOS, MSAS, Galileo-ready E1B/C
Компьютерная платформа	Intel Edison — dual-core 500MHz
Интерфейсы	I2C, UART, GPIO, TimeStamp, OTG USB, Bluetooth, Wi-Fi, GNSS
Антенна	Tallysman TW4721 Dual Feed GPS/BeiDou/Galileo/GLONASS
Размеры	26х36 мм
Вес	13 г

Кому может пригодиться подобное устройство? Как уже говорилось выше, создателям различной мобильной робототехники, автономной и не очень; причем, учитывая его низкую стоимость (предзаказ $545 за двойной набор и $285 за одинарный) не только профессиональным, но и энтузиастам. Далее, составителям различного рода карт, опять-таки, в том числе и любителям. Ну и просто занудам, желающим знать свое местоположение с точностью до сантиметра.

Создатели Reach, компания Emlid, удачно выступили на сайте indiegogo: меньше чем за месяц собрана почти двойная запрошенная сумма. Значит, проект непременно будет реализован. У вас еще есть время, чтобы сделать предзаказ и оказаться в числе первых, кто получит принципиально новое навигационное устройство. Рассылка товара запланирована на июль.

Источник

Точность измерений и погрешности в физике — определение и формулы с примерами

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):

(5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины: и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

• Для линейки 1:
• Для линейки 2:
• Для линейки 3:

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Определение площади и объема
• Связь физики с другими науками
• Макромир, мегамир и микромир в физике
• Пространство и время
• Как зарождалась физика
• Единая физическая картина мира
• Физика и научно-технический прогресс
• Физические величины и их единицы измерения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник