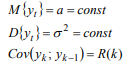Что значит ряд стационарен

Стационарные временные ряды — понятия и факторы

Содержание:

Эконометрика — это наука о построении, анализе и выполнении математических моделей реальных экономических явлений на основе реальных статистических данных.

Одним из важнейших направлений эконометрики является построение прогнозов по различным экономическим показателям. Основной задачей эконометрики является применение статистических и математических методов для эмпирического представления и подтверждения или опровержения результатов экономической теории.

Однако математические методы также используются в математической экономике для представления результатов экономической теории. Разделение «сфер интересов» эконометрики и математической экономики является разницей в критериях качества полученных моделей. В эконометрике, чем лучше построена модель, тем лучше она описывает имеющиеся эмпирические данные. В математической экономике подгонка модели под эмпирические данные не всегда говорит нам о ее качестве, и наоборот, не всегда нужно добиваться такой подгонки.

Использование статистических методов для анализа экономических данных имеет долгую историю. Отмечается, что первое эмпирическое исследование спроса (Шарль Давенант, 1699 г.) было опубликовано более трех веков назад, а первое современное исследование (Родульфо Энини, 1907 г.) — в начале 20 в. Сильным толчком к развитию эконометрики стало основание в 1930 г. Эконометрического общества, а в январе 1933 г. — выход в свет первого номера журнала «Econometrica». Основной целью Общества, как было определено в первом номере журнала, было «. изучение возможностей сочетания теоретико-количественного и эмпирико-количественного подходов к экономическим проблемам и распространение конструктивных и точных методов анализа, аналогичных тем, которые в настоящее время доминируют в естественных науках».

Однако в экономике существует несколько видов количественного анализа, ни один из которых не должен ассоциироваться с эконометрикой в отдельности. Таким образом, эконометрика — это не экономическая статистика. Эконометрика также не является подполем общей экономической теории, хотя большая часть экономической теории определенно носит количественный характер. Слово «эконометрика» также не является просто синонимом фразы «применение математики в экономике». Как показал опыт, все эти три дисциплины — статистика, экономическая теория и математика — необходимы, но ни одна из них сама по себе не является достаточной для истинного понимания количественных отношений в современной экономике. Ключом к этому является объединение всех трех этих дисциплин. Именно их объединение является предметом эконометрики.

Основные понятия теории временных рядов

Временной ряд — это последовательность чисел (измерений) экономического или бизнес-процесса во времени. Его элементы измеряются в последовательных точках во времени, как правило, через равные промежутки времени.

Обычно числа, составляющие временной ряд, или элементы временного ряда, нумеруются в соответствии с количеством точек во времени, к которым они относятся. Поэтому важен порядок расположения элементов временного ряда.

Расширенное понятие временных рядов. Временные ряды часто интерпретируются очень широко. Например, могут быть одновременно записаны несколько характеристик процесса, на который делается ссылка. В данном случае мы говорим о многомерных временных рядах. Когда измерения являются непрерывными, их называют непрерывными временными рядами или случайными процессами. Наконец, текущая переменная может быть не временной, а иной, например, пространственной. В данном случае мы говорим о случайных полях. Примеры временных рядов. В экономике это ежедневные цены акций, обменные курсы валют, еженедельные и ежемесячные объемы продаж, годовые объемы производства и др.

Считается, что временной ряд является стационарным, если числовые характеристики ряда являются постоянными в каждом сегменте временного ряда. На самом деле это не так, но есть методы, которые могут преобразовать временной ряд и сделать его стационарным.

Стационарность — это упрощение модели после увеличения конечной последовательности наблюдений до бесконечной.

Факторы, влияющие на построение временных рядов

Построение эконометрической модели включает два типа данных:

Первый тип включает в себя данные, характеризующие набор объектов в определенный момент времени;
Второй тип включает в себя данные, характеризующие один объект в нескольких последовательных точках времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, основанные на втором типе данных, называются моделями временных рядов.

Временной ряд определяется как набор значений конкретного индикатора за несколько последовательных точек во времени или периодов времени.

Формирование каждого уровня временных рядов основано на влиянии большого количества факторов, которые условно делятся на следующие группы:

• Факторы, формирующие тренд (Тренд Т);
• Факторы, формирующие циклические колебания серии. Это сезонные компоненты S;
• Случайные факторы (E).

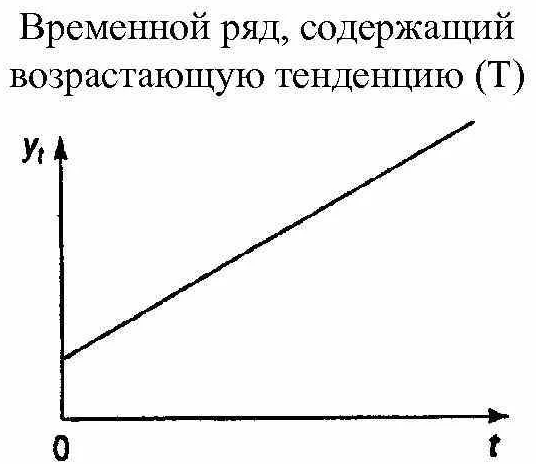
Многие временные ряды экономических показателей имеют тенденцию, характеризующую кумулятивное долгосрочное влияние факторов на изменение исследуемого показателя. В индивидуальном порядке все факторы могут оказывать одинаковое влияние на изучаемый показатель. Однако вместе они образуют нарастающую или убывающую тенденцию индикатора. На рисунке 1 показан пример временного ряда, содержащего восходящий тренд.

Рисунок 1: Пример временного ряда, содержащего восходящий тренд.

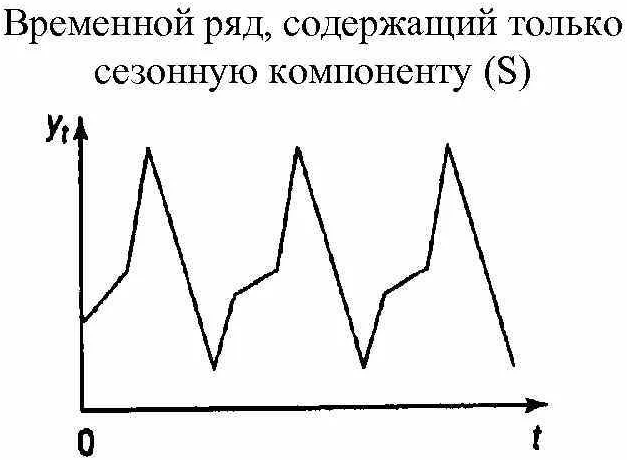
Индикаторы могут также подвергаться циклическим колебаниям. Такие колебания могут быть сезонными, связанными с общими изменениями конъюнктуры рынка и т.д. На рисунке 2 показан пример временного ряда с сезонной составляющей.

Рисунок 2: Пример временного ряда с сезонной составляющей.

Стационарные временные ряды

Отдельные временные ряды не имеют ни трендовой, ни циклической составляющей, каждый из их ближайших уровней равен сумме среднего уровня ряда и случайной составляющей (положительной или отрицательной). Такие серии называются стационарными. Если серия состоит из двух или трех компонентов, то она называется нестационарной.

Наиболее важными характеристиками стационарного ряда являются дисперсия и математическое значение ожидания.

Математическое ожидание процесса X(t) является неслучайной функцией M(t), которая равна математическому ожиданию в момент времени t. Дисперсия стационарного ряда представляет собой неслучайную функцию D(t), равную дисперсии в момент времени t.

Самый простой пример стационарного временного ряда — «белый шум», т.е. случайный процесс, в котором в разных временных точках значения независимы и равномерно распределены (рис. 3).

Рисунок 3: «Белый шум».

Ряд y(t) строго стационарен, если совместное распределение m наблюдений y(t1),y(t2). y(tm+1) не зависит от изменения времени, т.е. совпадает с распределением.

Ряд y(t) является слабо стационарным, если ожидаемое значение, дисперсия и ковариация не зависят от времени.

Рисунок 4: Формула.

В случае нарушения любого из вышеперечисленных условий серия не является стационарной.

Если есть строгая стационарность, то подразумевается слабая стационарность.

Стационарность может быть разбита как по математическому ожидаемому значению, так и по дисперсии.

Временной ряд y(t) является стационарным по отношению к детерминистическому ряду f(t), если ряд (yt-f(t)) является стационарным. Если y(t) является стационарным по отношению к детерминистическому тренду, то данный ряд относится к классу рядов, являющихся стационарными по отношению к детерминистическому тренду, т.е. это ряд TS.

Если эконометрическая модель формируется на основе временных рядов, принадлежащих к различным типам стационарности, то может быть сформирована неадекватная модель и условия OLS не выполняются. В результате не соблюдаются условия объективности, эффективности и согласованности полученных оценок.

Рекомендую подробно изучить предметы:

Экономическая теория Экономика

Ещё лекции:

• Демонетизация металлов — этапы и сущность
• Теории оборотного капитала — сущность, структура и определения
• Монополия на экономическом рынке — определение, концепция и виды
• Промышленная экономическая политика — концепция, основные инструменты и цели
• Общественное состояние государства — существо, характеристики, понятие и основные принципы
• Менеджмент в информационной экономике — управление, характер, концепция и функции
• Субъекты региональной экономической политики — концепция, цели, задачи и определения
• Экономика потребительской кооперации — преимущества, концепция и тенденции развития

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Стационарные временные ряды

Вы будете перенаправлены на Автор24

Стационарность — это упрощение модели после увеличения конечной последовательности наблюдений до бесконечной.

Факторы, влияющие на построение временного ряда

Построение эконометрической модели связано с двумя типами данных:

• К первому типу относятся данные, которые характеризуют совокупность объектов в определенное время;
• Ко второму типу относятся данные, которые характеризуют один объект за несколько последовательных временных моментов.

Модели, строящиеся по данным первого типа, носят название пространственные модели. А модели, построенные на основании данных второго типа – это модели временных рядов.

Под временным рядом понимается совокупность значений конкретного показателя за несколько последовательно происходящих моментов или временных периодов.

Формирование каждого уровня временного ряда основано на воздействии большого количества факторов, условно разделяемых на следующие группы:

1. Факторы, которые формируют тенденцию (тренд Т);
2. Факторы, которые формируют циклические колебания ряда. Это сезонная компонента S;
3. Случайные факторы (E).

Многие временные ряды экономических показателей имеют тенденцию, которая характеризует совокупное долгосрочное воздействие факторов на изменение исследуемого показателя. Все факторы по отдельности могут с равной силой воздействовать на изучаемый показатель. При этом в совокупности они образуют возрастающую или же убывающую тенденцию показателя. На рисунке 1 представлен пример временного ряда, который содержит возрастающую тенденцию.

Рисунок 1. Пример временного ряда, который содержит возрастающую тенденцию. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Показатели также могут быть подвержены циклическим колебаниям. Такие колебания бывают сезонными, связанными с общим изменение рыночной конъюнктуры и т.д. На рисунке 2 представлен пример временного ряда, содержащего сезонную компоненту.

Рисунок 2. Пример временного ряда, содержащего сезонную компоненту. Автор24 — интернет-биржа студенческих работ

Стационарные временные ряды

Отдельные временные ряды не имеют тенденции или циклической компоненты, каждый их следующий уровень равен сумме среднего уровня ряда и случайной компоненты (положительной или отрицательной). Такие ряды носят название стационарные. Если же ряды в своем составе содержат две или три компоненты, то называются нестационарными.

Важные характеристики стационарного ряда – это дисперсия и математическое ожидание.

Математическое ожидание процесса X(t) – это неслучайная функция M(t), которая равна в момент времени t математическому ожиданию. Под дисперсией стационарного ряда понимается неслучайная функция D(t), которая равна дисперсии в момент времени t.

Простейший пример стационарного временного ряда – это «белый шум», т.е. случайный процесс, в котором в разные моменты времени значения независимы и распределены одинаково (Рисунок 3).

Рисунок 3. «Белый шум». Автор24 — интернет-биржа студенческих работ

Ряд y(t) строго стационарен при условии, что совместное распределение m наблюдений y(t1),y(t2),…,y(tm+1) не зависит от изменения времени, другими словами, совпадает с распределением.

Ряд y(t) является слабо стационарным при условии, что математическое ожидание, дисперсия и ковариация не зависимы от временного момента.

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Если же одно из представленных выше условий нарушается, то ряд будет нестационарным.

При строгой стационарности подразумевается слабая стационарность.

Стационарность может быть нарушена как по математическому ожиданию, так и по дисперсии.

Временной ряд y(t) будет стационарным по отношению к детерминированному ряду f(t), в случае, если ряд (yt-f(t)) стационарен. Когда ряд y(t) стационарен по отношению к некоторому детерминированному тренду, то данный ряд относится к классу рядов, стационарных по отношению к детерминированному тренду, т.е. является TS рядом.

Если построение эконометрической модели осуществляется по временным рядам, которые принадлежат различным типам стационарности, то может получиться неадекватная модель и для нее не будут выполняться предпосылки МНК. Это станет причиной невыполнения условий несмещенности, эффективности и состоятельности полученных оценок.

Источник

Временные ряды-Введение

Дата публикации Jun 5, 2019

временная последовательностьпоследовательность данных, упорядоченная по времени. Временной ряд добавляет явную зависимость порядка между наблюдениями: измерение времени. В обычном наборе данных машинного обучения набор данных представляет собой набор наблюдений, которые обрабатываются одинаково при прогнозировании будущего. Во временных рядах порядок наблюдений является источником дополнительной информации, которую следует проанализировать и использовать в процессе прогнозирования. Предполагается, что временные ряды генерируются через регулярные интервалы времени (например, дневная температура) и поэтому называютсярегулярные временные ряды, Но данные во временном ряду не обязательно должны поступать через регулярные промежутки времени. В таком случае это называетсянерегулярные временные ряды, В нерегулярных временных рядах данные следуют временной последовательности, но измерения могут не происходить через регулярные интервалы времени. Например, данные могут быть сгенерированы как пакет или с различными временными интервалами[1], Пополнение счета или снятие средств с банкомата являются примерами нерегулярных временных рядов.

Временные ряды могут иметь одну или несколько переменных, которые меняются со временем.
Если есть только одна переменная, изменяющаяся во времени, мы называем этоОдномерный временной ряд, Если существует более одной переменной, она называетсяМногомерный временной ряд.Например, трехосевой акселерометр. Есть три переменные ускорения, по одной для каждой оси (х, у, г) и они меняются одновременно с течением времени.

Приложения временного ряда

Временные ряды используются в различных областях, таких как математические финансы, производство, данные о событиях (например, потоки кликов и события приложений), данные IoT и, как правило, в любой области прикладной науки и техники, которая включает временные измерения. СУБД временных рядов (система управления базами данных) являются наиболее быстро растущим сегментом в отрасли баз данных, что может свидетельствовать о растущей потребности в прогнозировании временных рядов в отрасли.

Анализ временных рядов

Анализ временных рядов извлекает значимую статистику и другие характеристики набора данных, чтобы понять его. Анализ временных рядов может помочь сделать более точные прогнозы, но это не обязательно является основной целью анализа. На практике подходящая модель подбирается для данного временного ряда и (в случае контролируемого обучения) соответствующие параметры оцениваются с использованием известных значений данных[3], Процесс анализа временных рядов состоит из методов, которые пытаются понять природу ряда и часто полезны для будущего прогнозирования и моделирования. Эта область исследования ищет «ЗачемЗа набором данных временного ряда.

Прогнозирование временных рядов

Прогнозирование временных рядов включает в себя подбор моделей на основе исторических данных (обучающий набор) и их использование для прогнозирования будущих наблюдений (тестовый набор). На первом этапе прошлые наблюдения собираются и анализируются для разработки подходящей математической модели, которая фиксирует основной процесс создания данных для ряда. На втором этапе будущие события прогнозируются с использованием модели. Этот подход особенно полезен, когда не хватает удовлетворительной объяснительной модели. Прогнозирование будущего называется экстраполяцией в классической статистической обработке данных временных рядов. Более современные области фокусируются на теме и называют ее прогнозированием временных рядов. Навык модели прогнозирования временных рядов определяется ее будущей эффективностью прогнозирования. Прогнозирование временных рядов имеет важные приложения в различных областях. За последние несколько десятилетий исследователи приложили много усилий для разработки и совершенствования подходящих моделей прогнозирования временных рядов. Это часто происходит за счет возможности объяснить, почему был сделан конкретный прогноз, доверительные интервалы и даже лучше понять причины, лежащие в основе проблемы.

Типы временных рядов

Детерминированный временной ряд

Детерминированный временной ряд — это тот, который может быть явно выражен аналитическим выражением. У него нет случайных или вероятностных аспектов. В математическом плане это можно описать точно за все время в терминах разложения в ряд Тейлора при условии, что все его производные известны в некоторый произвольный момент времени. Его прошлое и будущее полностью определяются ценностями этих производных в то время. Если это так, то мы всегда можем предсказать его будущее поведение и указать, как он вел себя в прошлом.

Недетерминированный временной ряд

Недетерминированный временной ряд — это тот, который не может быть описан аналитическим выражением. У него есть некоторый случайный аспект, который мешает его поведению быть описанным явно. Временной ряд может быть недетерминированным, потому что:

1. Вся информация, необходимая для ее явного описания, недоступна, хотя в принципе может быть.
2. Природа процесса генерации по своей природе случайна.

Поскольку недетерминированные временные ряды имеют случайный аспект, он следует вероятностным законам Таким образом, данные определяются статистическими терминами, то есть распределениями вероятностей и средними значениями различных форм, таких как средние значения и дисперсии.

Стационарные временные ряды

Стационарный временной ряд — это такой, статистические свойства которого, такие как среднее значение, дисперсия, автокорреляция и т. Д., Не зависят от времени. Стационарный ряд относительно легко предсказать: вы просто прогнозируете, что его статистические свойства в будущем будут такими же, как и в прошлом. Таким образом, большинство статистических методов прогнозирования основаны на предположении, что временные ряды являются приблизительно стационарными.

большинство статистических методов прогнозирования предполагают, что ряды могут быть (приблизительно) стационарными с помощью математических преобразований.

Нестационарные временные ряды

Нестационарный ряд — это тот, статистические свойства которого меняются со временем. Существует множество способов нестационарности временных рядов, таких как изменение дисперсии, сдвиги уровней, сезонность в 6-й момент и т. Д. Вот наиболее распространенные модели нестационарности:

Трендовый компонент:Тенденция показывает общую тенденцию увеличения или уменьшения данных в течение длительного периода времени. Тенденция — это плавная, общая, долгосрочная, средняя тенденция. Не всегда необходимо, чтобы увеличение или уменьшение было в одном и том же направлении в течение данного периода времени.[8], Если временной ряд не показывает возрастающую или убывающую модель, то ряд в среднем является стационарным.

Циклический компонент:Любой паттерн, показывающий движение вверх и вниз вокруг данного тренда, идентифицируется как циклический паттерн. В циклическом паттерне движения вверх и вниз не происходят через постоянные промежутки времени, их невозможно предсказать.

Сезонная составляющая:Если пики и провалы серии происходят через равные промежутки времени, модель называется сезонной (например, продажи мороженого).

Случайный компонент:Остаток — это то, что осталось, когда все шаблоны были удалены. Остатки — это случайные колебания. Вы можете думать о них как о компоненте шума.

летний

Большинство статистических методов прогнозирования основаны на предположении, что временные ряды являются приблизительно стационарными. Стационарный ряд относительно легко предсказать: вы просто прогнозируете, что его статистические свойства в будущем будут такими же, как и в прошлом. Анализ моделей временных рядов является первым шагом преобразования нестационарных данных в стационарные данные (например, путем удаления трендов), чтобы можно было применять методы статистического прогнозирования.[5], Существует три основных шага построения модели временных рядов качественного прогнозирования: обеспечение стационарности данных, выбор правильной модели и оценка точности модели.

Источник