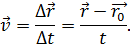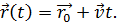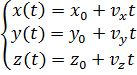Что значит рпд физика

Прямолинейное равномерное движение — формулы, уравнения и примеры

Общие сведения

Под движением в физике понимают изменение координат тела относительно других объектов с течением времени. Раздел, который изучает происходящее, называется кинематикой. Эта наука исследует только процессы перемещения, не беря во внимание причин его вызвавшего. Часто за тело принимается материальная точка, физическими размерами которой пренебрегают. Это возможно, так как любой объект можно рассматривать как совокупность связанных точек.

Систему, состоящую из неподвижных относительно друг друга тел, можно рассматривать как начало отсчёта при движении. Для этого составляется группа уравнений, которые определяют, как изменяется положение перемещающейся точки с течением времени. Другими словами, определяют координаты тела для любого момента. Называют их уравнениями движения. В декартовых координатах система выглядит так: x = f1 (t); y = f2 (t); z = f3 (t).

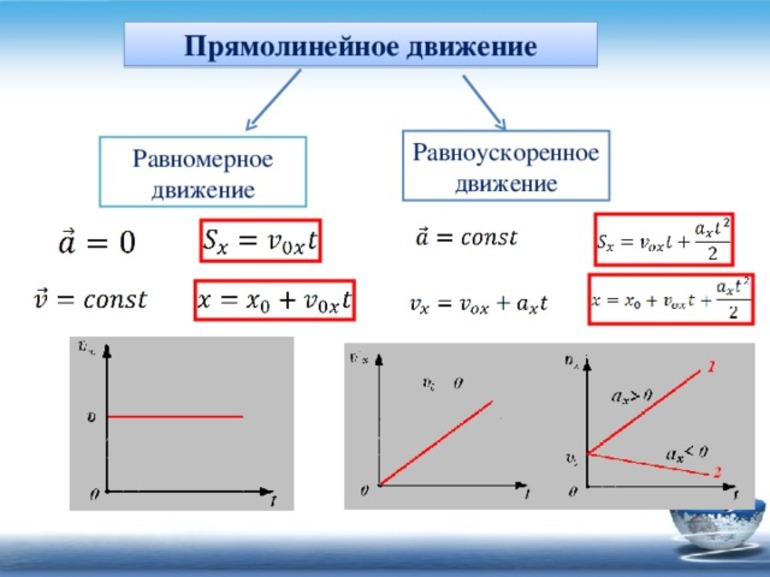
Существуют следующие виды движения:

• равномерное прямолинейное;
• равноускоренное;
• перемещение по окружности;
• гармонические колебания.

Все эти изменения положения в пространстве отличаются по виду скорости, ускорения и принципа смены координат. Линия, по которой перемещается материальная точка, называется траекторией движения. По сути, это пройденный телом путь. При криволинейном перемещении, в отличие от прямолинейного, модуль движения всегда будет превышать путь. Это связано с тем, что расстояние, пройденное по дуге всегда будет больше стягивающей хорды.

Рассматривая перемещающиеся тела через одинаковые временные промежутки, можно выделить равномерные и неравномерные движения. Кроме этого, существуют перемещения тела параллельно самому себе — поступательные. Криволинейное движение можно рассматривать как самостоятельный вид изменения положения, а можно свести его к сумме движений по дугам окружностей с различными радиусами кривизны.

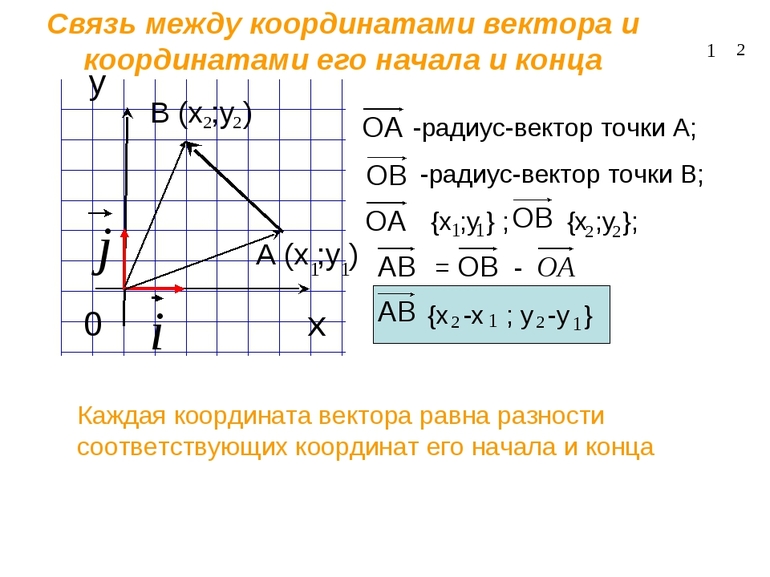
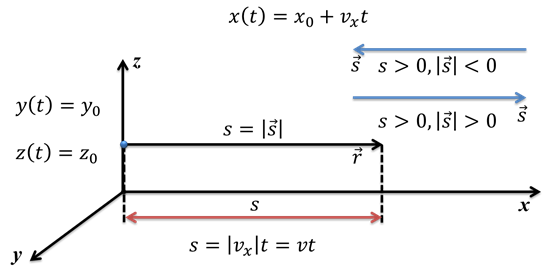
При исследовании движения часто измеряют быстроту смены положения, то есть скорость. Если моменту времени соответствует радиус-вектор движущегося тела, то за малый промежуток времени материальная точка переместится на расстояние: Δs = Δr = r2 — r1. Но для характеристики перемещения используют не саму скорость, а её среднее значение: Vср = Δs / Δt.

Принцип исследования перемещения

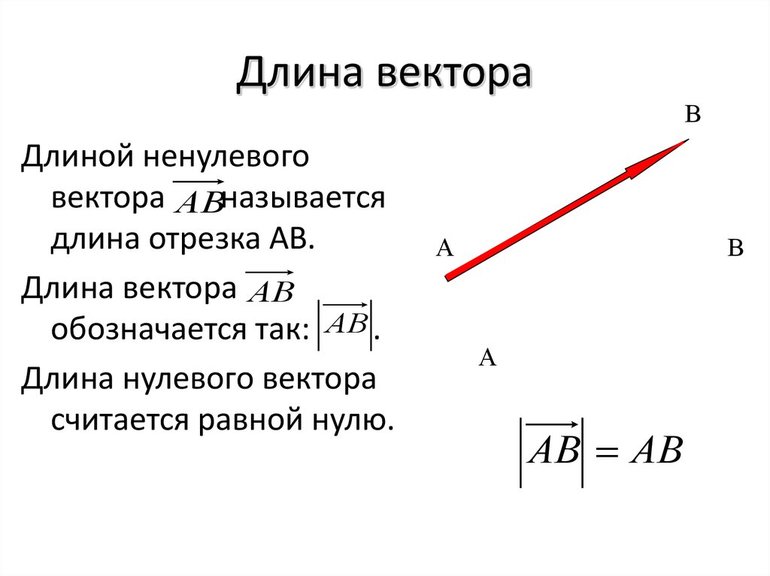
Для того чтобы изучить движение тела в пространстве, нужно выбрать систему отсчёта. Пусть имеется тело, находящееся в точке А. Через некоторое время оно переместилось в точку В. Эти две координаты можно соединить прямым отрезком, являющимся вектором перемещения S. Так как известно, где находилось тело вначале и S, то можно определить его положение в любое время вне зависимости от вида передвижения тела.

В механике работают не с самим вектором, а его проекцией. Поэтому для исследования изменения положения нужно выбрать систему координат. За неё принимаются оси ординаты и абсциссы. Тогда начальное положение можно задать как X0 и Y0, а конечное X, Y. Решение основной задачи механики заключается в возможности указать положение в любой момент времени. То есть найти x (t) и y (t). Для этого понадобится знать X0 и Y0.

Эти значения являются фиксированными и не зависят от времени. Совершённое перемещение можно описать как раз с помощью проекции разности конца положения и начала: X — X0 = Sx; Y — Y0 = Sy. Отсюда можно вывести фундаментальное правило нахождения изменения положения для любой точки времени:

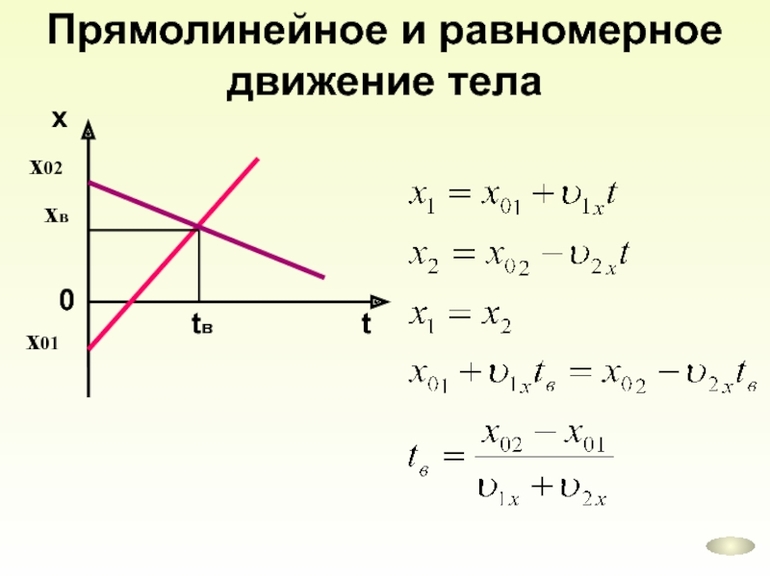
Таким образом, чтобы исследовать прямолинейное равномерное движение, нужно решить систему уравнений, а для этого необходимо знать начальное положение и изменение проекции перемещения тела с течением времени на координатную ось.

Под равномерным движением понимается перемещение, когда тело за любые промежутки времени проходит равное расстояние. Прямолинейным оно является тогда, когда точка проходит путь по прямой линии. Значит, если за любые равные промежутки времени тело, совершает одинаковое перемещение, то пройденный путь называют РПД (равномерно-прямолинейным). Например, за Δ t равное единице тело преодолеет расстояние равное S1, за Δt2 соответственно S2. Получается, что вектор перемещения материальной точки всегда направлен в одну сторону и имеет один и тот же модуль.

Следует отметить, что характеристикой такого изменения положения является скорость РПД. Для её определения используется отношение вектора перемещения точки к времени, за которое оно произошло: V = S / t, При этом в формуле время может иметь любое значение. Оно является скалярной величиной и неизменным. Значит, скорость РПД можно описать постоянным вектором, сонаправленным с перемещением вектора расстояния.

Нахождение вектора

Чтобы решить главную задачу механики относительно РПД, нужно воспользоваться формулой для нахождения вектора скорости. Из этого определения следует, что S = V * t. Известно, что если имеется соотношение векторов, то его же можно использовать для их проекций на координатные оси. Значит, Sx = Vx * t и Sy = Vy * t. Следовательно, если известны проекции скорости, то можно определить и вектор проекции перемещения в любое время. Отсюда следует, что решение основной задачи для РПД будет иметь вид:

Эти два уравнения всегда нужно рассматривать в совокупности, так как положение тела задаётся на плоскости двумя координатами. Но на самом деле такой системой пользоваться не очень удобно. Поэтому на практике применяют упрощённое выражение.

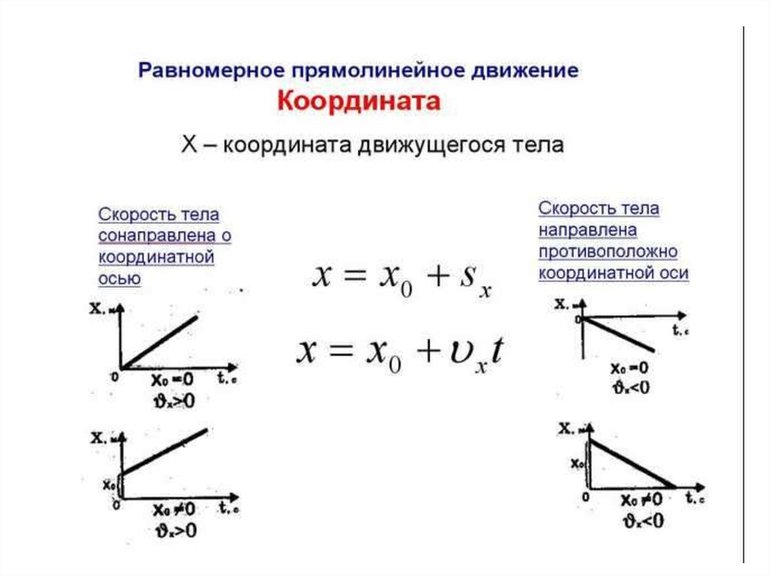
Икс и игрек нулевые зависят от значений координат. Формула изменит вид в зависимости от того, какие выбрать за начальные. Так, выражение значительно упростится, если вектор скорости будет направлен вдоль одной из координатных осей. В результате тело будет лежать на одной из них в начальный момент.

Например, пусть это будет ось икс. Если её расположить так, что она будет размещена параллельно вектору скорости, то ось игрек будет ему перпендикулярна. Смещая координатные оси, точку начального положения можно поместить на ось абсциссы. Для такой повёрнутой системы совокупность уравнений РПД будет также справедливым. Но игрек начальный для рассматриваемой системы будет равняться нулю. Ему же будет равна и проекция скорости на ординату. Учитывая это система главных выражений примет вид:

Фактически получился частный случай общего вида решения основной задачи механики. Так как второе уравнение никакой информации не даёт (тождественный ноль), то его можно убрать. Отсюда следует, что РПД рационально описывать, направляя координатную ось вдоль вектора скорости и выбирать начальное положение точки на координатной прямой.

Тогда получается упрощённый вариант главной формулы: x (t) = x0 + Vx + t. При этом направление вектора скорости значение не имеет. По нему он может как совпадать с осью, так и быть ей противоположным. Нужно отметить, что Vx является проекцией и может быть положительной или отрицательной величиной. В первом случае тело движется вдоль координатной прямой, а во втором в противоположном её направлении.

Решение задач

Физика — это наука, которая позволяет не только знать какие-либо законы и определения, но и учит использовать их на практике. Самостоятельное решение примеров позволяет закрепить имеющиеся знания. Существуют типовые задания, с помощью которых можно проработать изученный материал. Вот некоторые из них:

1. Определить, какие из далее приведённых формул описывают прямолинейное равномерное движение и какие из них не могут быть применимы к перемещению: S = 5 — 2t; V = 5 — 2t. Для того чтобы можно было дать ответ нужно вспомнить формулы, описывающие РПД: x = x0 + Vx * t и Sx = Vx * t. Если рассмотреть второе выражение, то можно утверждать, что x0 = 5, а Vx = -2. Отсюда следует, что оно полностью соответствует условию для РПД. В первом же выражении находится модуль вектора перемещения. Если t = 0 (в начальный момент времени), то S = 5. Такого быть не может, значит, формула не имеет смысла.
2. При движении вдоль оси икс координата точки за первые пять секунд изменилась от десяти метров до минус десять. Найти модуль скорости и проекцию. Для решения за основу берётся главная формула ПРД: x (t) — x0 = Vx * t. Отсюда Vx = (x (t) — x0) / t. Применительно к исходным данным она будет иметь вид: Vx = (x1 — x0) / t = (-10м — 10м) / 5 с = — 4 м / с. Так как тело движется вдоль прямой икс, то модуль скорости будет равняться минус проекции. Значит |V| = 4 м / с. Закон же, описывающий движение, будет следующим: x (t) = 10 — 4 * t.
3. Собака бежит за велосипедистом по прямолинейному участку шоссе. Движение человека описывается уравнением x1 = 25 + 10 * t, а животного x2 = -35 + 12 * t. Узнать, догонит ли собака велосипедиста. Можно предположить, что четвероногий друг догонит едущего на велосипеде. Чтобы это подтвердить нужно, определить, когда настанет этот момент. Итак, для того чтобы собака догнала велосипедиста она должна изначально быть сзади него и бежать с большей скоростью. Так как в начальный момент координата человека равна 25, а животного — 35, то собака сзади, при этом 12t > 10t. Условия выполняются, а значит предположение верное. Встреча же их должна произойти в один и тот же момент времени Tвст. Значит, 25 + 10 * Tвст = — 35 + 12 * Tвст → 60 = 2 * Tвст → Tвст = 30 секунд.

Таким образом, решение задач на ПРД требует логического мышления и знания нескольких формул. Кроме этого, можно использовать и графическое описание, то есть изображать график движения тела на координатной плоскости. Для этого в формулу подставляют значения и строят по результатам зависимость.

Источник

Уравнение РПД

Урок 5. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Уравнение РПД»

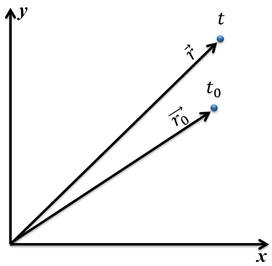
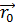
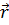
Мы знаем, что в каждый момент времени, положение точки задаётся радиус-вектором. Пусть в момент времени t₀, начальное положение точки задаёт радиус-вектор . Во все последующие моменты времени положение точки будет описываться радиус-вектором .

Исходя из определения скорости равномерного прямолинейного движения, запишем:

Как правило, начальный момент времени — это точка отсчёта, поэтому примем t₀ = 0. Если мы теперь выразим 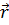из полученного выражения, то получим функцию зависимости радиус-вектора от времени:

Это и есть уравнение равномерного прямолинейного движения. То есть, если нам известно начальное положение точки и скорость её движения, то мы сможем найти радиус-вектор в каждый момент времени.

Вместо векторного уравнения можно использовать уравнение для каждой из координат:

Поскольку пройденный путь — это изменение координаты х в данном случае, мы можем найти его, используя модуль скорости. Заметим, что числовые значения пройденного пути и перемещения будут совпадать при прямолинейном движении. Только не стоит забывать, что пройденный путь — это скалярная величина, которая не может быть отрицательной.

Перемещение же, легко может быть отрицательным, если точка двигается в направлении, противоположном направлению координатной оси.

Итак, мы выяснили, что для описания равномерного прямолинейного движения достаточно получить уравнение для одной координаты. Давайте рассмотрим, как будут выглядеть графики функций зависимости скорости и координаты от времени. Начнём с простого: при равномерном движении скорость постоянна. Поэтому график зависимости скорости от времени будет представлять собой прямую горизонтальную линию.

Иными словами, при равномерном движении скорость не зависит от времени, так как является константой. Заметим, что если мы рассмотрим конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты х. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а длина другой — это время.

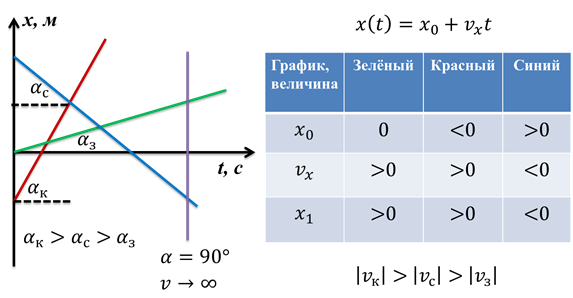
Рассмотрим теперь несколько графиков зависимости координаты от времени. На рисунке вы видите три прямых, каждая из которых описывается одним и тем же уравнением.

Точки пересечения этих графиков с осью х соответствуют значениям начального положения х₀. Как видно из графика, для зелёной прямой х₀ = 0, для синей прямой х₀ > 0, а для красной — х₀ Оцените видеоурок

Источник