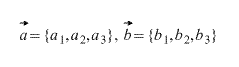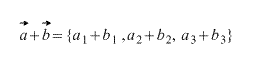Что значит результирующий вектор

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

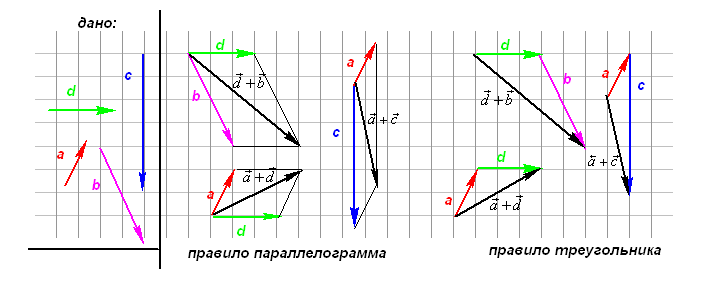
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

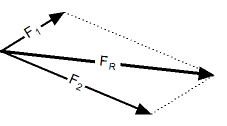Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

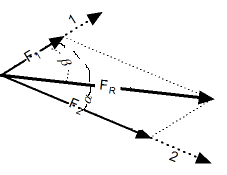Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Источник

Результирующий вектор: расчет, примеры, упражнения

Содержание:

В результирующий вектор — это результат, полученный с помощью операции с векторами, результатом которой также является вектор. Обычно эта операция представляет собой сумму двух или более векторов, с помощью которой получается вектор с эквивалентным эффектом.

Таким образом получаются такие векторы, как результирующая скорость, ускорение или сила. Например, когда на тело действует несколько сил. F₁, F₂, F₃,…. векторная сумма всех этих сил равна чистой силе (равнодействующей), которая математически выражается следующим образом:

F₁ + F₂ + F₃ +… = F_р или F_N

Результирующий вектор, будь то силы или любая другая величина вектора, находится с применением правил сложения векторов. Поскольку векторы имеют направление и смысл, а также числовое значение, недостаточно добавить модули, чтобы получить результирующий вектор.

Это верно только в том случае, если задействованные векторы направлены в одном направлении (см. Примеры). В противном случае необходимо использовать методы векторной суммы, которые в зависимости от случая могут быть геометрическими или аналитическими.

Примеры

Геометрическими методами нахождения результирующего вектора являются метод траверса и метод параллелограмма.

Что касается аналитических методов, существует метод компонентов, с помощью которого можно найти вектор, полученный из любой системы векторов, при условии, что у нас есть его декартовы компоненты.

Геометрические методы сложения двух векторов

Предположим, что векторы или Y v (Мы обозначили их жирным шрифтом, чтобы отличить их от скаляров). На рисунке 2а) они расположены на плоскости. На рисунке 2 б) он переведен в вектор v таким образом, что его начало совпадает с концом или. Результирующий вектор идет от начала координат первого (или) до кончика последнего (v):

Результирующая фигура в этом случае представляет собой треугольник (треугольник — это 3-сторонний многоугольник). Если у нас есть два вектора в одном направлении, процедура такая же: поместите один из векторов за другим и нарисуйте тот, который идет от начала или хвоста первого до конца или конца последнего.

Обратите внимание, что порядок, в котором выполняется эта процедура, не имеет значения, поскольку сумма векторов коммутативна.

Также обратите внимание, что в этом случае модуль (длина или размер) результирующего вектора — это сумма модулей добавленных векторов, в отличие от предыдущего случая, когда модуль результирующего вектора меньше суммы модулей участников.

Метод параллелограмма

Этот метод очень подходит, когда вам нужно добавить два вектора, исходные точки которых совпадают, скажем, с началом системы координат x-y. Предположим, что это так для наших векторов или Y v (рисунок 3а):

На рисунке 3b) параллелограмм построен с помощью пунктирных линий, параллельных или уже v. Результирующий вектор имеет начало в точке O и конец в точке пересечения пунктирных линий. Эта процедура полностью эквивалентна описанной в предыдущем разделе.

Упражнения

-Упражнение 1

Учитывая следующие векторы, найдите результирующий вектор с помощью метода обхода.

Решение

Метод траверса — первый из известных. Помните, что сумма векторов коммутативна (порядок слагаемых не влияет на сумму), поэтому вы можете начать с любого из векторов, например или (рисунок 5а) или р (рисунок 5b):

Полученная фигура представляет собой многоугольник, а результирующий вектор (синий) называется р. Если вы начнете с другого вектора, сформированная форма может быть другой, как показано в примере, но результирующий вектор будет таким же.

Упражнение 2.

На следующем рисунке известно, что модули векторов или Y v соответственно они равны u = 3 условных единицы и v = 1,8 условных единиц. Угол, который или форма с положительной осью абсцисс составляет 45º, а v образует 60º с осью Y, как показано на рисунке. Найдите результирующий вектор, величину и направление.

Решение

В предыдущем разделе результирующий вектор был найден методом параллелограмма (на рисунке выделен бирюзовым цветом).

Простой способ найти результирующий вектор аналитически — выразить слагаемые векторы через их декартовы компоненты, что легко, когда известны модуль и угол, например векторы в этом примере:

или_Икс = u. cos 45º = 3 x cos 45º = 2,12; или_Y = u. грех 45º = 3x грех 45º = 2,12

v_Икс = v. sin 60º = 1,8 x sin 60º = 1,56; v_Y = -v. cos 60º = -1,8 x cos 60º = — 0,9

Векторы или Y v это векторы, принадлежащие плоскости, поэтому каждый из них имеет по две компоненты. Вектор u находится в первом квадранте, а его компоненты положительны, а вектор v — в четвертом квадранте; его компонент x положительный, но его проекция на вертикальную ось падает на отрицательную ось y.

Вычисление декартовых компонент результирующего вектора

Результирующий вектор находится путем алгебраического сложения соответствующих компонентов x и y, чтобы получить их декартовы компоненты:

р_Икс = 2.12 + 1.56 = 3.68

Как только декартовы компоненты указаны, вектор становится полностью известным. Полученный вектор можно записать в квадратных скобках (подтяжки):

R = условные единицы

Обозначение в квадратных скобках используется для отличия вектора от точки на плоскости (или в пространстве). Другой способ выразить полученный вектор аналитически — использовать единичные векторы я и j в плоскости (я, j Y k в пространстве):

р = 3.68 я + 1.22 j условные единицы

Поскольку обе компоненты результирующего вектора положительны, вектор р принадлежит к первому квадранту, который ранее уже был замечен графически.

Величина и направление результирующего вектора

Зная декартовы компоненты, величина R вычисляется по теореме Пифагора, так как полученный вектор рвместе со своими компонентами R_Икс и R_Y образуют прямоугольный треугольник:

Величина или модуль: R = (3.68 2 + 1.22 2 ) ½ = 3.88

Направление q, взяв за основу положительную ось x: q = arctan (R_Y / Р_Икс) = arctg (1,22 / 3,68) = 18,3 º

Источник

Физика

Тестирование онлайн

Вектор

Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.

Если начало вектора совпадает с его концом, получим нулевой вектор.

Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.

На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону

Вектор -c — это вектор c, но противоположного направления. Тогда

Проекция вектора

Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение — в противоположном случае.

Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: s_x=x-x₀, на ось ОУ: s_y=y-y₀.

Частные случаи, когда проекция на ось Ox или Oy нулевая.

Сумма составляющих вектора по осям равна данному вектору, т.е.

Сложение векторов

Правило параллелограмма: диагональ параллелограмма — сумма двух векторов с общим началом.

Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.

Рассмотрим правила на примерах.

Вычитание векторов

Вычитание векторов — это сумма положительного и отрицательного вектора.

Упражнения

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник