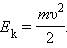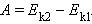Что значит результирующая сила

Результирующая сила: как она рассчитывается и решаются упражнения

Содержание:

В прочность в результате это сумма всех сил, действующих на одно и то же тело. Когда на тело или объект действует одновременно несколько сил, возникает эффект. Действующие силы можно заменить одной силой, которая производит такой же эффект. Эта единственная сила является результирующей силой, также известной как чистая сила, и обозначается символом F_р.

Эффект, который он производит F_рэто будет зависеть от его размера, направления и смысла. Физические величины, имеющие направление и смысл, являются векторными величинами.

Как силы, действующие на вектор тела, равнодействующая сила F_р это векторная сумма всех сил, которую можно графически представить стрелкой, указывающей ее направление и направление.

С помощью равнодействующей силы проблема тела, на которое действует несколько сил, упрощается, сводя ее к единственной действующей силе.

Формула

Математическое представление результирующей силы — это векторное суммирование сил.

F_р= Результирующая сила

∑F = Сумма сил

N= Количество сил

Результирующая сила также может быть представлена ​​уравнением второго закона Ньютона.

а = ускорение тела

Если уравнение (1) подставить в уравнение (3), будут получены следующие уравнения:

∑F = м.к (4)

Математические выражения (4) и (5) предоставляют информацию о состоянии тела, получая вектор ускорения к.

Как рассчитывается результирующая сила?

Результирующая сила получается путем применения Второго закона Ньютона, который гласит следующее:

Чистая сила, действующая на тело, равна произведению его массы и ускорения, которое оно приобретает.. (Уравнение (3))

Ускорение тела будет иметь направление приложенной чистой силы. Если все силы, действующие на тело, известны, достаточно добавить их векторно, чтобы получить результирующую силу. Точно так же, если известна равнодействующая сила, достаточно разделить ее на массу тела, чтобы получить его ускорение.

Если результирующая сила равна нулю, тело находится в состоянии покоя или с постоянной скоростью. Если на тело действует одна сила, результирующая сила равна этой силе F_р=F.

Когда несколько сил действуют на одно и то же тело, необходимо учитывать компоненты вектора силы, независимо от того, параллельны ли эти силы или нет.

Например, если мы сдвигаем книгу по столу горизонтально, силы в горизонтальном направлении — единственные, которые обеспечивают ускорение телу. Чистая вертикальная сила, действующая на книгу, равна нулю.

Если сила, приложенная к книге, имеет наклон по отношению к горизонтальной плоскости стола, сила записывается как функция вертикальной и горизонтальной составляющих.

Результат параллельные силы

Параллельные силы, действующие на тело, — это силы, действующие в одном направлении. Они могут быть двух типов равного или противоположного смысла.

Когда силы, действующие на тело, имеют одинаковое направление и одинаковое направление или имеют противоположное направление, результирующая сила получается путем выполнения алгебраической суммы численных значений сил.

Непараллельные силы

Когда к телу прилагаются непараллельные силы, равнодействующая сил будет иметь прямоугольную и вертикальную составляющие. Математическое выражение для расчета чистой силы:

∑ F_Икс и ∑ F_Икс= Алгебраическое суммирование компонентов Икс а также Y приложенных сил

θ_Икс= угол, образованный равнодействующей силой F_р с валом Икс

Обратите внимание, что результирующая сила выражения (6) не выделена жирным шрифтом, потому что она выражает только числовое значение. Направление определяется углом θ_Икс.

Выражение (6) справедливо для сил, действующих в одной плоскости. При действии сил в пространстве учитывается составляющая z силы, если вы работаете с прямоугольными компонентами.

Решенные упражнения

Параллельные силы одного направления складываются и вычитаются с параллельной силой противоположного направления.

F_р= 63 Н + 50 Н — 35 Н = 78 Н

Результирующая сила имеет величину 78 Н в горизонтальном направлении.

2. Вычислить равнодействующую силу тела под действием двух сил. F_{1 Y} F₂. Сила F₁ он имеет магнитуду 70 Н и наносится горизонтально. Сила F₂ он имеет магнитуду 40 Н и применяется под углом 30 ° к горизонтальной плоскости.

Для решения этого упражнения строится диаграмма свободного тела с осями координат. Икс а также Y

Все компоненты определены Икс а также Y сил, действующих на тело. Сила F₁ имеет только одну горизонтальную составляющую на оси Икс. Сила F₂он состоит из двух компонентов F_2xи F_{2 и} которые получаются из функций синуса и косинуса угла 30 °.

После определения результирующих сил на валу Икс а также Y переходим к получению численного значения равнодействующей силы.

Результирующая сила — это квадратный корень из суммы квадратов компонентов сил.

Угол, образованный равнодействующей силой F_р получается из следующего выражения:

Результирующая сила F_р он имеет звездную величину 106,53N и имеет направление, определяемое углом 10,82 °, который он образует с горизонтом.

Ссылки

1. Дола, Дж., Даффи, М. и Персиваль, А. Физика. Испания: Хайнеманн, 2003.
2. Ависон, Дж. Х. Мир физики. Индия: Томас Нельсон и сыновья, 1989.
3. Пинсент, М. Физические процессы. Соединенное Королевство: Нельсон Томас, 2002.
4. Ядав, С.К. Инженерная механика. Дели: Издательство Discovery, 2006.
5. Серуэй Р. и Джуэтт Дж. У. Физика для ученых и инженеров. Калифорния, США: Брукс / Коул, 2010.

Лекарство от сна: что это такое, как его использовали и почему не рекомендуется

Зеленый стул: причины, состояния и методы лечения

Источник

Результирующая сила. Кинетическая энергия. Работа результирующей силы.

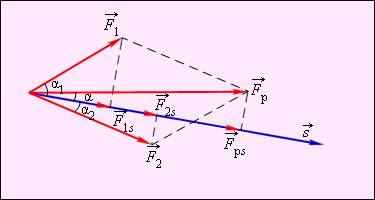
Результирующая сила – это векторная сумма всех сил, действующих на данное тело.

Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от 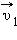до то силы совершили определенную работу A.

Работа всех приложенных сил равна работе равнодействующей силы

Работа равнодействующей силы.

A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α

Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы В этом случае векторы силы перемещения скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой

Отсюда следует, что

Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.

Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью 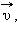равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

Закон сохранения энергии при абсолютно упругом и абсолютно неупругом ударе.

Закон сохранения механической энергии

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии эта работа равна изменению кинетической энергии:

Или Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии

Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения.

Дата добавления: 2018-08-06 ; просмотров: 2783 ; Мы поможем в написании вашей работы!

Источник

Результирующая сила

В классической физике , то результирующая сила является векторной суммой всех сил о том , что тело подвергается . Математически сила, возникающая в результате воздействия на систему n сил, записывается: F → р <\ displaystyle <\ vec > _ >

F → р знак равно ∑ я знак равно 1 нет F → я знак равно F → 1 + F → 2 + . . . + F → нет <\ displaystyle <\ vec > _ = \ sum _ ^ <\ vec > _ = <\ vec > _ <1>+ <\ vec > _ <2>+ . + <\ vec > _ >

Как и другие силы, результирующая сила имеет величину и ориентацию . Его также можно определить как общую силу, действующую на объект, когда все силы, действующие на него, складываются.

За исключением случаев, когда на объект действует единственная сила, результирующая сила не соответствует «реальной» силе.

Резюме

Параллельные силы

Когда сила A и сила B действуют на объект в одном направлении (коллинеарные векторы), результирующая сила ( C ) равна A + B в направлении A и B. Если сила A имеет более чем интенсивность чем сила B , результирующая будет ближе к точке приложения A, чем к точке приложения B.

180 ° силы

Когда сила A и сила B действуют на один и тот же объект, но в противоположных направлениях (180 градусов между двумя векторами — антипараллельные векторы ), результирующая ( C ) равна | A — B |, в том же смысле, что и сила большей нормы .

Непараллельные силы

Когда угол между силами отличается от упомянутых выше случаев, силы должны складываться с использованием параллелограмма сил .

Например, возьмем фигуру 3. Эта конструкция даст тот же результат, если мы переместим F ₂ так, чтобы его конец соответствовал началу F ₁ , и если мы возьмем результирующую как вектор, соединяющий конец F ₁ с концом. из F ₂ . Эту процедуру можно повторить, чтобы добавить F ₃ к полученному F ₁ + F ₂ и так далее. См., Например, рисунок 4.

Составные части

Также возможно разложить силы на их декартовы компоненты, чтобы определить компоненты вектора результирующей силы. Чтобы сделать это, мы должны добавить различные компоненты одной и той же плоскости, чтобы найти результирующий компонент для этой плоскости, а затем повторить процесс для каждой плоскости, на которую действуют исследуемые силы.

Итак, если сила равна сложению двух сил и в плоскости xy, то р → <\ displaystyle <\ vec >> В → <\ displaystyle <\ vec >> B → <\ displaystyle <\ vec >>

р Икс знак равно В Икс + B Икс <\ displaystyle R_ = A_ + B_ >

р y знак равно В y + B y <\ Displaystyle R_ = A_ + B_ >

Затем соотношение Пифагора используется для определения модуля результирующей силы.

р знак равно р Икс 2 + р y 2 <\ displaystyle R = <\ sqrt ^ <2>+ R_ ^ <2>>>>

Примечания и ссылки

Приложения

Статьи по Теме

Библиография

: документ, использованный в качестве источника для этой статьи.

Харрис Бенсон (в переводе — Марк Сеген, Бенуа Вильнев, Бернар Маршетер и Ричард Ганьон), Physique 1 Mécanique , Édition du Renouveau Pédagogique, 2009 г. , 4- е изд. , 465 с.

Источник

Читайте также:  Что значит шунтирует кнопку