Что значит рейтинговое голосование

Статья 37. Количественное, рейтинговое, альтернативное и качественное голосование

Статья 37. Количественное, рейтинговое, альтернативное и качественное голосование

1. Количественное голосование представляет собой выбор варианта ответа: «за», «против» или «воздержался». Подсчет голосов и предъявление результатов голосования производятся по каждому голосованию.

2. Рейтинговое голосование представляет собой ряд последовательных количественных голосований по каждому из вопросов, в которых может принять участие каждый депутат. При этом предъявление результатов голосования по каждому голосованию производится только по окончании голосования по всем вопросам. Если по итогам рейтингового голосования несколько вопросов набрали достаточное для их принятия число голосов, то принятым считается решение по вопросу, набравшему наибольшее число голосов. Если по итогам рейтингового голосования ни один из вопросов не набрал достаточного для принятия числа голосов, то на повторное голосование ставится вопрос, набравший наибольшее число голосов. Решение по нему считается принятым, если при голосовании он набрал достаточное для принятия число голосов.

3. Альтернативное голосование представляет собой голосование только за один из вариантов вопроса, поставленного на голосование. Подсчет голосов и предъявление результатов голосования производятся одновременно по всем вариантам вопроса, поставленного на голосование.

4. Качественное голосование представляет собой альтернативное голосование с качественной оценкой поставленного на голосование вопроса по одному из вариантов: «удовлетворительно», «неудовлетворительно».

Откройте актуальную версию документа прямо сейчас или получите полный доступ к системе ГАРАНТ на 3 дня бесплатно!

Если вы являетесь пользователем интернет-версии системы ГАРАНТ, вы можете открыть этот документ прямо сейчас или запросить по Горячей линии в системе.

Источник

Что такое рейтинговое голосование?

Рейтинговое голосование – что это такое?

Существует несколько систем голосования, которые используются на онлайн-площадках, а также и в более серьезных мероприятиях, например, при выборе президента России.

Более привычной системой голосования является так называемая количественная – когда победитель определяется путем выбора того, за кого проголосовал наибольший процент участников (более половины или же, если планка в 50% отсутствует, то просто большая часть).

Однако более эффективной системой является рейтинговая. Ее отличие в том, что кандидаты при голосовании не просто оцениваются по количеству отданных за них голосов. Каждый голосующий еще и указывает, на какое место бы поставил каждого из кандидатов: первое, второе и так далее.

Схема рейтингового голосования

В основе рейтингового голосования, как становится ясно из названия, лежит сам по себе рейтинг. Рейтинги могут выглядеть подобным образом (проводилось голосование с участием кандидатов A, B, C, D):

Это чисто рейтинговое голосование, где по итогам мероприятия определяется только позиция кандидата в общем рейтинге. Такой тип используется, например, если проводится опрос среди потребителей, какой продукт из представленных им нравится больше всего. Но зачастую по итогам рейтингового голосования отображаются еще и проценты (от общего числа проголосовавших):

Как видно из данного рейтинга, кандидат C получил в целом больше голосов, чем кандидаты A и B – 40%, в то время как они удостоились лишь 25% каждый. Если бы проводилось количественное голосование, C оказалась бы на первой позиции.

Однако при сборе голосов по системе рейтинга участника не просто просят отметить наиболее подходящего кандидата, но и требуют проставить их в порядке убывания. Вот как примерно может выглядеть бюллетень, заполненный по системе рейтинга:

Как проводится итоговый выбор кандидата путем рейтингового голосования

Выбор может строиться на разных дополнительных подсистемах. Например:

• Чтобы победить, кандидат обязан набрать более 50% голосов. Голосование проводится снова и снова до тех пор, пока не будет набран такой процент. В таком случае рейтинговая система позволяет отсечь тех кандидатов, которые были поставлены участниками на низшие позиции. Например, во втором туре кандидат D из приведенного выше примера выбывает, и борьба сохраняется только между вариантами A, B, C. Выбывание может проводиться до тех пор, пока не останется только 2 участника, после чего будет определен лучший, или же остановиться, например, когда на выбор осталось 3 позиции (тогда по итогам голосования будет установлено 1, 2 и 3 место).
• Нет необходимости набирать 50%. В таком случае голосование может проводиться всего в один тур. Независимо от набранных процентов, победителем становится тот кандидат, которого чаще всего ставили на первые позиции.

Пример первой схемы рейтингового голосования – это лонг-лист и шорт-лист в некоторых творческих конкурсах.

Жюри ставит всех участников в порядке убывания, где первый – самый достойный выигрыша, последний – самый не достойный. Затем рейтинги всех членов жюри сверяются и составляется единый, основанный на среднем арифметическом позиций каждого кандидата.

Из 100 участников выбирается 50 (лонг-лист), которые принимают участие в первой туре борьбы за приз. Затем вновь начинается установка рейтинга, и составляется уже шорт-лист (обычно 25 вариантов). Последний этап – голосование на выбор лучших кандидатов из шорт-листа.

Второй вариант применяется реже и в менее важных делах. Например, компания хочет определить направление дальнейшего развития и спрашивает у потребителей, какой товар они бы хотели в дальнейшем видеть в продаже. Здесь достаточно одного тура голосования, чтобы оценить, что понравится клиентам, а что выпускать в продажу не стоит.

Когда эффективно рейтинговое голосование

Наиболее эффективным рейтинговое голосование оказывается в тех ситуациях, когда голосующим приходится выбирать из нескольких похожих вариантов. Имеет смысл составлять рейтинг, если выбор сыграет важную роль. Простой пример: при выборе президента в «гонке» участвуют два демократа и коммунист.

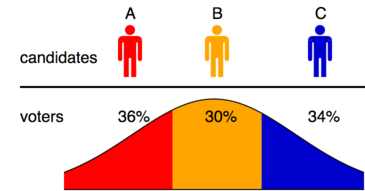
В целом жители страны настроены таким образом: 60% – за демократию, 40% – за коммунизм. Однако из-за наличия сразу двух представителей-демократов 60% демократов могут разделиться на два потока, например, отдав 25% одному человеку и 35% – другому.

Получится, что кандидат-коммунист будет выбран 40% (так как у него нет конкурентов) и по итогам количественного голосования займет первое место. Конечно, это не устроит демократов, которых в стране большинство.

Чтобы такое не происходило, целесообразнее было бы учредить голосование с системой рейтинга. Тогда результаты будут таковы:

В итоге в качестве президента будет выбран демократ, что больше устроит население.

Источник

Рейтинговое голосование — Ranked voting

Рейтинговое голосование, также известное как голосование с ранжированным выбором или преимущественное голосование , относится к любой системе голосования, в которой избиратели используют ранжированное (или преимущественное) голосование для выбора более чем одного кандидата (или другой альтернативы, по которой проводится голосование) и ранжирования этих выборов в последовательность по порядковой шкале: 1-е, 2-е, 3-е и т. д. Рейтинговое голосование отличается от кардинального голосования , при котором кандидаты оцениваются независимо, а не ранжируются. Наиболее важные различия между системами ранжированного голосования заключаются в методах, используемых для принятия решения о том, какой кандидат (или кандидаты) избран из данного набора бюллетеней. Некоторые из наиболее важных методов описаны ниже.

Еще одно (более косметическое) отличие заключается в формате бюллетеней. Некоторые юрисдикции требуют, чтобы избиратели оценивали всех кандидатов; некоторые ограничивают число людей, которые могут быть ранжированы; а некоторые позволяют избирателям ранжировать столько, сколько они считают нужным, а остальные объединяются в конце. Другие правила (иногда связанные с методом определения победителя) применяются в разных случаях.

Предмет этой статьи не следует путать с мгновенным вторым голосованием , особой формой рейтингового голосования, которому американская организация FairVote присвоила название «голосование с ранжированным выбором». Рейтинговое голосование используется на национальных выборах или выборах штатов в Австралии, Ирландии, Великобритании (ассамблея Шотландии и Уэльса), двух штатах США, Мальте, Словении и Науру . Он также используется для городских выборов в Новой Зеландии, Канаде и США (Кембридж, Массачусетс и Нью-Йорк).

СОДЕРЖАНИЕ

История рейтингового голосования

Первое известное обсуждение рейтингового голосования встречается в трудах майоркца Рамона Лулля в конце 13 века. Его смысл не всегда ясен, но считается, что он отстаивал то, что теперь известно как метод Коупленда (реализованный посредством последовательности двусторонних выборов, а не рейтинговых бюллетеней для выбора).

Его произведения привлекли внимание Николая Кузанского в начале 15 века. На Николаса они, похоже, не слишком повлияли, и он независимо придумал то, что сейчас называется подсчетом Борды, отстаивая реализацию посредством ранжированных бюллетеней. Сочинения Ллулла и Николаса были утеряны и вновь всплыли в двадцатом веке.

Современное изучение этого предмета началось, когда Жан-Шарль де Борда опубликовал в 1781 году статью, в которой пропагандировался метод, который теперь ассоциируется с его именем. Этот метод вызвал критику со стороны маркиза де Кондорсе , который разработал критерий признания коллективного предпочтения и заметил, что метод Борды не всегда его удовлетворяет (на примере, который остается спорным: см. Сравнение избирательных систем ).

Интерес к этой теме возродился в девятнадцатом веке, когда датчанин Карл Андро изобрел систему STV, которая была немедленно принята в его родной стране и заново изобретена Томасом Хэром в Великобритании в 1857 году. Уильям Роберт Уэр предложил вариант IRV, который выигрывал в одиночку, примерно в 1870 году. , возможно, не подозревая, что Кондорсе ранее упоминал об этом, но только чтобы осудить это. В последующие годы английский математик Чарльз Лютвидж Доджсон (более известный как Льюис Кэрролл ) и англо-австралиец Эдвард Нэнсон опубликовали новые методы голосования.

Теоретическое моделирование избирательных процессов началось с работы Дункана Блэка 1948 года , за которой вскоре последовала работа Кеннета Эрроу о согласованности критериев голосования. С тех пор эта тема привлекала внимание ученых в рамках теории социального выбора , обычно относящейся к экономике.

Теоретические свойства рейтингового голосования

Критерий Кондорсе

Некоторые концепции, разработанные маркизом де Кондорсе в восемнадцатом веке, до сих пор играют центральную роль в этой теме.

Если есть кандидат, которого большинство избирателей на выборах предпочитает любому другому кандидату, то этот кандидат известен как победитель по Кондорсе . Метод голосования, при котором всегда выбирается победитель Кондорсе, если таковой имеется, называется последовательным по Кондорсе или (что эквивалентно) удовлетворяющим критерию Кондорсе . Методы с этим свойством известны как методы Кондорсе .

Если на выборах нет победителя Кондорсе, то должен быть цикл Кондорсе , что можно проиллюстрировать на примере. Предположим, что есть 3 кандидата, A, B и C, и 30 голосующих, из которых 10 голосуют C – B – A, 10 голосуют B – A – C и 10 голосуют A – C – B. Тогда нет победителя Кондорсе. В частности, мы видим , что А не может быть победителем Кондорсе , потому что 2 / +3 избирателей предпочитают B в A; но В не может быть победителем Кондорсе , потому что 2 / 3 предпочитают C к В; и C не может быть победителем Кондорсе , потому +2 / +3 предпочитают от А до С , но не может быть победителем Кондорсе . Таким образом , поиск победитель Кондорсе берет нас в кругах никогда не найти один.

Пространственные модели

Пространственная модель представляет собой модель избирательного процесса , разработанного Дункана Блэка и продлен Энтони Даунс . Предполагается, что каждый избиратель и каждый кандидат занимают место в пространстве мнений, которое может иметь одно или несколько измерений, и предполагается, что избиратели предпочитают более близкого из двух кандидатов более удаленному. Политический спектр является простой пространственной моделью в одном измерении.

Бюллетень	Считать
A – B – C	36
B – A – C	15
B – C – A	15
C – B – A	34

На схеме показана простая пространственная модель в одном измерении, которая будет использована для иллюстрации методов голосования далее в этой статье. Предполагается, что сторонники A голосуют за A – B – C, а сторонники C голосуют за C – B – A, в то время как сторонники B делятся поровну между теми, кто имеет A и C в качестве второго предпочтения. Если имеется 100 избирателей, то количество поданных бюллетеней будет определяться позициями избирателей и кандидатов в спектре в соответствии с приведенной таблицей.

Пространственные модели важны, потому что они являются естественным способом визуализации мнений избирателей и потому, что они приводят к важной теореме, теореме о медианном избирателе , также созданной Блэком. Он утверждает, что для широкого класса пространственных моделей, включая все одномерные модели и все симметричные модели в более высоких измерениях, гарантированно существует победитель Кондорсе и кандидат, ближайший к медиане распределения избирателей.

Если мы применим эти идеи к диаграмме, мы увидим, что действительно есть победитель Кондорсе — В — который предпочтительнее А на 64% и С на 66%, и что победитель Кондорсе действительно является кандидатом, ближайшим к медиане распределение избирателей.

Другие теоремы

Теорема о невозможности Эрроу проливает более пессимистический свет на рейтинговое голосование. В то время как теорема о медианном избирателе говорит нам, что для многих наборов предпочтений избирателя легко разработать метод голосования, который работает идеально, теорема Эрроу утверждает, что невозможно разработать метод, который идеально работает во всех случаях.

Чем ближе пессимизм Эрроу или оптимизм Блэка к истине электорального поведения, это вопрос, который необходимо определить эмпирически. Ряд исследований, в том числе статья Тайдмана и Плассмана, предполагают, что простые пространственные модели типа, удовлетворяющие теореме о медианном избирателе, близко соответствуют наблюдаемому поведению избирателей.

Другой пессимистический результат, теорема Гиббарда (принадлежащая Аллану Гиббарду ), утверждает, что любая система голосования должна быть уязвима для тактического голосования — тема, которая здесь не обсуждается.

Граф Борда

Кандидат	Счет
А	87
B	130
C	83

Подсчет Борда присваивает баллы каждому кандидату, добавляя количество баллов, присужденных каждым бюллетенем. Если есть m кандидатов, то кандидат, занявший первое место в бюллетене, получает m — 1 баллов, второй — m — 2 и так далее, пока кандидат, занявший последнее место, не получит ни одного балла . В примере B выбран 130 из 300 очков.

Подсчет Борда прост в применении, но он не удовлетворяет критерию Кондорсе. Его особая слабость состоит в том, что на его результат может сильно повлиять выдвижение кандидатов, которые сами не имеют никаких шансов быть избранными.

Другие позиционные системы

Системы голосования, которые присуждают баллы таким образом, но, возможно, используют другую формулу, известны как позиционные системы . Если вектор оценок ( m — 1, m — 2, . 0) соответствует счету Борда, (1, 1 ⁄ 2 , 1 ⁄ 3 , . 1 / m ) определяет систему Даудалла и ( 1, 0, . 0) соответствует FPTP .

Альтернативное голосование

Мгновенное голосование

1-й тур 2-й тур 3-й тур 36 A – B – C A – C А 15 B – A – C A – C А 15 B – C – A C – A А 34 C – B – A C – A А

Мгновенное голосование (IRV) исключает кандидатов в серии раундов, имитируя влияние отдельных бюллетеней на сокращающийся набор кандидатов. Первый тур состоит из фактически поданных бюллетеней. Поскольку никто не имеет большинства голосов при первом подсчете, определяется кандидат с наименьшим количеством предпочтений за первое место (в данном случае B) и удаляется из бюллетеней для последующих раундов. Его или ее голоса передаются согласно следующему отмеченному предпочтению, если таковое имеется. Таким образом, во втором туре бюллетени выражают предпочтение только двум кандидатам (чаще m — 1). Мы останавливаемся на этом, потому что A определен как победитель, поскольку он является предпочтением большинства избирателей.

Системы исключения являются относительно неуклюжими в реализации, поскольку каждый бюллетень необходимо повторно проверять в каждом раунде, а не допускать вычислений на основе простой таблицы производных статистических данных. IRV не удовлетворяет критерию Кондорсе. В отличие от большинства рейтинговых систем голосования, IRV не допускает привязки предпочтений, за исключением случаев, когда избиратель предпочитает наименее предпочтительные кандидаты.

Единый передаваемый голос

Единственный передаваемый голос (STV) является multiwinner и пропорциональной версия н.с.в.. В соответствии с STV голос выборщика первоначально распределяется за его или ее наиболее предпочтительного кандидата. После того, как кандидаты были либо избраны ( победители ) путем достижения квоты, либо исключены ( проигравшие ), излишки голосов передаются от победителей к оставшимся кандидатам ( претендентам ) в соответствии с предпочтениями, упорядоченными избирателями. Он имеет различные методы определения передачи голосов.

Минимакс

А B C А — 36:64 51:49 B 64:36 — 66:34 C 49:51 34:66 —

Минимаксная система определяет результат путем построения таблицы результатов, в которой есть запись для каждой пары различных кандидатов, показывающая, как часто первый предпочтительнее второго. Таким образом, поскольку 51 избиратель предпочитает A вместо C, а 49 имеют противоположное предпочтение, запись (A, C) читается как «51: 49». В каждой строке мы определяем наименее благоприятный (т. Е. Минимальный) результат для первого кандидата (выделен жирным шрифтом), а выигравший кандидат — это тот, чей наименее благоприятный результат является наиболее благоприятным (т. Е. Максимальным). В этом примере победителем является B, наименее благоприятный результат которого — победа, а наименее благоприятный результат других кандидатов — несколько другие потери.

Определение минимаксного победителя из набора бюллетеней — особенно простая операция. Этот метод удовлетворяет критерию Кондорсе, и его можно рассматривать как выбор победителя Кондорсе, если он есть, и как выбор кандидата, который ближе всего подходит к победителю Кондорсе (при простой метрике) в противном случае.

Метод Ллулла / метод Коупленда

Кандидат	Счет
А	1
B	2
C	0

Метод Коупленда присваивает каждому кандидату оценку, полученную из таблицы результатов, как показано выше для минимакса. Оценка — это просто количество положительных результатов в ряду кандидата, т. Е. Количество других кандидатов, которым определенный кандидат предпочел большинство избирателей. Кандидат с наибольшим количеством очков (в данном случае B) побеждает.

Метод Коупленда прост и согласован с Кондорсе, но имеет недостаток, заключающийся в том, что для определенных моделей предпочтений избирателей без победителя Кондорсе он приведет к ничьей, какой бы большой ни был электорат. Поэтому его сторонники обычно рекомендуют использовать его вместе с тай-брейком. Подходящие правила для этой цели включают минимакс, IRV и счет Борда, последнее из которых дает метод Дасгупта-Маскина.

Другие методы

• Завершение Кондорсе выбирает победителя Кондорсе, если таковой имеется, в противном случае используется отдельная процедура для определения результата. Если счет Борды является запасным вариантом, мы получаем метод Блэка ; если мы используем н.с.в. мы получаем Тидеман в «Кондорсе-Заяц».

• Метод Кумбса представляет собой простую модификацию IRV, в которой кандидат, исключаемый в каждом раунде, является кандидатом с наибольшим количеством предпочтений на последнем месте, а не с наименьшим количеством предпочтений при первом месте (так что C, а не B, исключается в первом раунде примера и B — победитель). Метод Кумбса не является согласованным по Кондорсе, но, тем не менее, удовлетворяет теореме о медианном избирателе. У него есть недостаток, заключающийся в том, что он зависит, в частности, от предпочтений избирателей, занимающих последнее место, которые могут быть выбраны с меньшей осторожностью, чем их первые места.

• В методах Болдуина и Нансона используются более сложные правила исключения, основанные на счете Борда. Они последовательны по Кондорсе.

• Метод Кемени-Янга сложен, но совместим с Кондорсе.
• Метод Смита сокращает набор кандидатов до набора Смита , который представляет собой синглтон, включающий победителя Кондорсе, если он есть, и обычно меньше исходного набора. Обычно его рекомендуют использовать вместе с тай-брейком, причем наиболее распространенными являются IRV и минимакс. Это просто с вычислительной точки зрения, хотя и не интуитивно понятно для большинства избирателей.
• Контингент голосование является 2-круглая версия н.с.в. и дополнительное голосование является запретной форма условного голосования.
• Метод Баклина существует в нескольких формах, некоторые из которых совместимы с Кондорсе.
• Занимают метод пара , метод Шульца и метод разделения цикла являются Кондорс-последовательными методами средней сложности вычислений на основе анализа структуры цикла избирательных бюллетеней.
• Метод Доджсона известен главным образом тем, что был изобретен Льюисом Кэрроллом . Он согласован по Кондорсе, но сложен в вычислительном отношении.

Сравнение рейтинговых методов голосования

Самая простая форма сравнения — аргументация на примере. Пример в данной статье иллюстрирует то, что многие люди считают слабым местом IRV; другие примеры показывают предполагаемые недостатки других методов.

Логические критерии голосования можно рассматривать как экстраполяцию характерных черт примеров в бесконечное пространство выборов. Последствия часто трудно предсказать: изначально приемлемые критерии противоречат друг другу и отвергают в остальном удовлетворительные методы голосования.

Эмпирические сравнения могут быть выполнены с использованием смоделированных выборов. Популяции избирателей и кандидатов строятся на основе пространственной (или другой) модели, и точность каждого метода голосования, определяемая как частота, с которой он выбирает кандидата, ближайшего к центру распределения избирателей, может быть оценена случайными испытаниями. Методы Кондорсе (и метод Кумбса) дают лучшие результаты, за ними следует подсчет Борда, с некоторым отставанием IRV и худшим FPTP.

Математические свойства метода голосования должны быть сбалансированы с его прагматическими характеристиками, такими как его понятность для среднего избирателя.

Недостатки рейтингового голосования

Рейтинговое голосование позволяет получить больше информации о предпочтениях избирателей, чем при голосовании по протоколу FPTP, но это связано с определенными затратами. Избирателям приходится заполнять более сложные бюллетени для голосования, а процедура подсчета голосов — в зависимости от характера метода голосования — более сложная и медленная, часто требуя механической поддержки.

Источник