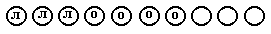Что значит решить задачу по вопросам

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л — лещи, о — окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

1) 3 + 4 = 7 (р.) — пойманные рыбы

Для ответа на вопрос задачи мы выполнили два действия.

Пусть х — пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х — все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

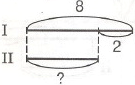
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Методы решения задач: по действиям VS составление уравнения

Привычка страшная вещь, потому что действие совершается без осознания, что в некоторых ситуациях ведет к печальным последствиям. Например, я привыкла решать с детьми задачи, составляя уравнение и перестала оценивать другие возможности. А самое притягательное в том, этот метод проще объяснить. Четыре простых шага к успеху:

Выделить про какие величины/количества идёт речь в задачи и в каком отношении они находятся. Эта та самая пресловутая краткая запись, в форме таблицы, схемы или списка.

Одну из величин обозначить через переменную, а оставшиеся выразить через неё.

Найти, что можно приравнять, чтобы составить уравнение. Иногда в задаче написано, что какие-то две величины являются равными, в других случаях это может быть отношение больше на. /меньше на.

Решить уравнение и ответить на вопрос задачи.

Как это выглядит на практике:

Такая красивая и простая схема! Глаз радуется. С другой стороны, решение задач по действиям требует большего напряжения. Помимо того, чтобы выяснить какие величины есть в задаче и как они друг с другом соотносятся, нужно еще понять какие математические действия помогут найти что-то. Это значит, что должно быть понимание действий с точки зрения в каких ситуациях его можно применять и как интерпретировать результат. Например, сложение — используется для нахождения общего количества, равноименных величин. То есть нельзя складывать разные единицы измерения, ведь не понятно, что получится в итоге. Факт кажется очевидным, но я наблюдала огромное количество попыток сложить проценты с рублями, скорость с расстоянием и т.д. Но тут есть хитрость. Нельзя складывать яблоки с грушами, но можно объединить их всех в единый кластер фруктов и складывай сколько хочешь. А есть величины, которые не объединяются. Та же скорость и расстояние. Ничего общего. Подобные сложности возникают и с остальными операциями.

Если ребенок, при решении задачи, начал перебирать варианты действий с числами, значит он не понимает для чего нужна каждая арифметическая операция. После того как это удалось объяснить, встаёт проблема понимания математических отношений. Быть больше на какое-то количество, быть меньше на какое-то количество и самые страшные быть больше/меньше во сколько-то раз. Многие дети связывают эти отношения с операциями, больше на — сложение, меньше на — вычитание и т.д. Отчасти в этом есть смысл, но только пока мы решаем простые задачи. А такой вариант даётся с трудом:

Известно, что одно число больше другого на 12 или в 4 раза. Найдите эти числа.

Надо что-то сложить и умножить, но в задаче всего два числа и это может стать преградой. Когда спрашиваешь, что значит одно число больше другого на сколько-то или во сколько-то раз, видишь, что ребенок понятия не имеет. И начинаются пляски с бубном, рисование картин, в тщетной надежде связать математические операции с реальными ситуациями. Иногда возникает острое желание дать взрослым детям седьмого класса в руки счетные палочки и попросить считать на них.

Да, простые алгоритмы и схемы дают результат: ребенок окончит школу с достойным баллом по математике. Нужно ли что-то еще? Вопрос риторический. Для бодрости духа, стоит иногда устроить челлендж «Решаем задачи по действиям». Пока не дошли до квадратных уравнений это можно провернуть с любой задачей.

Источник

Что значит решить задачу по вопросам

ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА БУДУЩЕГО, ПРОВЕРЕННАЯ ПРОШЛЫМ

Этот сайт посвящен возрожденным классическим традициям образования.
С глубокой благодарностью к великим педагогам прошлого, оставившим нам это бесценное наследие.

АЛТУШКИНА ТАТЬЯНА АНАТОЛЬЕВНА

Руководитель проекта

Как перед многими мамами, передо мной когда-то встала проблема школьного обучения своих подросших детишек. Отдавать их в школу было безумно жалко. Я точно знала, что им там будет плохо, хотя и не могла тогда ясно сформулировать, почему…

ГОРЯЧЕВА ИРИНА АНАТОЛЬЕВНА

Разработчик филологического блока

Бывают ли в жизни чудеса.

В самом начале 2008 года мне позвонили из Екатеринбурга. За полторы тысячи километров от Москвы состоятельная многодетная мама, озадаченная образованием своих детишек, нашла мои публикации, посвящённые К. Д. Ушинскому, его учебным книгам, и обратилась ко мне за советами. Это был подарок свыше!

КОСТЕНКО ИГОРЬ ПЕТРОВИЧ

Разработчик математического блока, канд. физико-математич. наук, доцент

Более 140 опубликованных работ — научно-математических, научно-методических, историко-педагогических, в том числе учебник по теории вероятностей (изд. 2004 г. и 2012 г.) и монография «Проблема качества математического образования в свете исторической ретроспективы» (2013 г.).

НИФОНТОВА ЕЛИЗАВЕТА МИХАЙЛОВНА

Разработчик математического блока,
тренер-методист

Я работаю в Русской классической школе учителем математики и методистом уже более восьми лет. В эту школу я попала чудом, иначе не скажешь. Вспоминаю своё собеседование с учредителем школы — Татьяной Анатольевной.

БАЛАКАЕВ МИХАИЛ ГЕННАДЬЕВИЧ

Разработчик программ по истории

По образованию я юрист. Окончил Свердловский юридический институт по специальности «правоведение». После получения диплома работал в Институте философии и права УрО РАН. Потом судьба привела меня в школу, и я стал учителем истории.

МАЛЮГА НАТАЛЬЯ НИКОЛАЕВНА

Преподаватель начальной школы,

тренер-методист

Учителем начальных классов я работаю более 20 лет.

Начинала преподавать по программе традиционного обучения (математика М. И. Моро, Г. В. Бельтюкова; русский язык Т. Г. Рамзаевой, чтение М. И. Горецкого). Немного поработала и по программе «Школа 2100».

ШИПОВА НАТАЛЬЯ ВЯЧЕСЛАВОВНА

Преподаватель филологии,
тренер-методист

Выбрать профессию учителя — это взять на себя огромную ответственность за юные души твоих учеников, а учитель-словесник вдвойне в ответе за то, какими людьми станут его ученики, с каким отношением к жизни, к людям, к Родине они выйдут из школы.

КОЧЕВА НИНА ВАСИЛЬЕВНА

Педагог дошкольного и начального образования,
тренер-методист

Я начала работать по этой программе десять лет назад. За спиной у меня к этому времени был многолетний опыт работы в общеобразовательной школе. И я думаю, что именно он помешал мне сразу принять и оценить новую программу.

КОСТЕНКОВ ВЛАДИМИР АЛЕКСАНДРОВИЧ

Преподаватель

церковнославянского языка

По образованию я тренер-преподаватель. До работы в Русской классической школе был детским тренером по карате. Многого достиг как сам, будучи спортсменом, так и на тренерском поприще, и считал, что спорт — это призвание на всю мою жизнь…

ПЕТРОВА ГАЛИНА НИКОЛАЕВНА

Преподаватель филологии

По специальности я учитель английского и немецкого языков. В Русской классической школе работаю с 2011 года. Моё знакомство с РКШ началось с расписания уроков, которое я случайно увидела, будучи в гостях.

ВОЛКОВА ВЕРА БОРИСОВНА

Секретарь
Русской классической школы

Русская Классическая Школа стала частью моей жизни очень стремительно, буквально в течение одного дня.

Август 2012 года. Я уже полгода работаю секретарём в школе — приказы, документы, справки. А школа не обычная, средняя, а Русская классическая.

Источник

Задачи в косвенной форме. 1 класс.

Кроме простых задач в 1 классе, встречаются необычные задачи.

Например: «На столе 7 карандашей. Это на 4 карандаша больше, чем в коробке. Сколько карандашей лежит в коробке?»
В условии задачи сказано «больше», значит надо было бы складывать, а задача решается вычитанием (7 — 4 = 3).
Их называют «Задачи в косвенной форме».

Рассмотрим 2 задачи:

Задача 1.
У Оли зеленые и белые шарики. Зеленых – 10. Белых – на 2 больше, чем зеленых. Сколько белых шариков у Оли?

Задача 2.
У Оли зеленые и белые шарики. Зеленых – 10. Их на 2 больше, чем белых. Сколько белых шариков у Оли?

Задачи отличаются только одним словом. В первой задаче сказано «белых шариков больше, чем зеленых», а во второй, что «их больше, чем белых». Начертим схему и определим, большее или меньшее число нужно найти.

Задача 1.
Зеленых шариков 10, белых – неизвестно, но сказано, что на 2 больше, чем зеленых. Значит, ищем большее число.

Решение.
Так как белых шариков на 2 больше, значит, нужно будем складывать:
10 + 2 = 12 (ш.)
Ответ: у Оли 12 белых шариков.

Задача 2.
Первая часть данной задачи такая же первая часть задачи 1, зеленых шаров 10. «Их на 2 больше», слово «их» указывает на зеленые шары. Если зеленых шаров на 2 больше, значит, белых на 2 меньше, чем зеленых.

Решение.
Нам нужно найти меньшее число, значит, нужно вычитать:
10 – 2 = 8 (ш.)
Ответ: у Оли 8 белых шариков.

Задача 3. Маша сорвала с веточки 5 слив. Она сорвала на 3 меньше, чем Света. Сколько слив сорвала Света?
Разбираем задачу:
Слово «она» указывает на Машу. Маша сорвала на 3 меньше, чем Света. Значит, Света сорвала на 3 больше, чем Маша. Начертим схему:

Так как Маша сорвала больше слив, ищем большее число, значит, нужно выполняем сложение.

5 + 3 = 8 (с.)
Ответ: Света сорвала 8 слив.

Задача 4. В одной вазе 7 яблок. Это на 4 яблока больше, чем на тарелке. Сколько яблок лежит на тарелке?
В условии задачи есть слово «ЭТО» указывает вазу: если в вазе на 4 яблока больше, значит, на тарелке на 4 яблока меньше.
Схема к задаче:

На 2 меньше – без двух столько же.
Если меньше, надо вычитать.
Решение:
7 – 4 = 3 (яб.)
Ответ: 3 яблока лежит на тарелке.

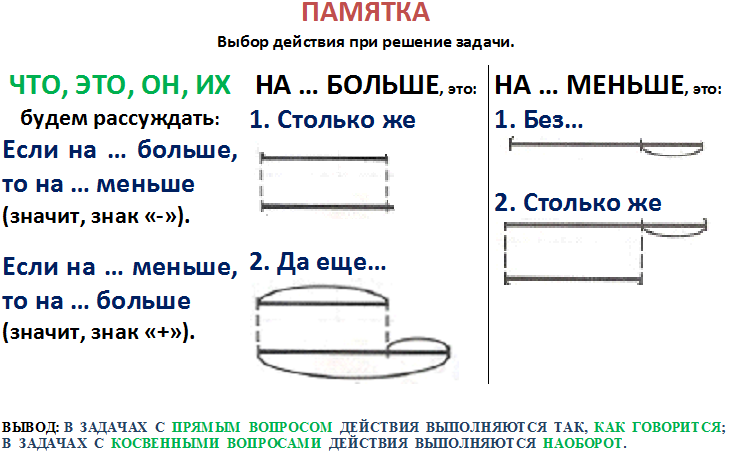
При решении задачи в косвенной форме важно помнить, что если одно число на несколько единиц больше, то другое на столько же единиц меньше.

Для того, чтобы правильно проанализировать задачу, воспользуйся памяткой.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 72

Источник