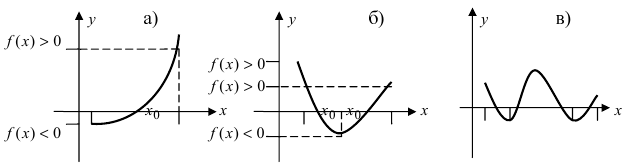- РАЗРЫВНАЯ ФУНКЦИЯ
- Смотреть что такое «РАЗРЫВНАЯ ФУНКЦИЯ» в других словарях:
- Непрерывность функций и точки разрыва с примерами решения
- Непрерывность функций и точки разрыва
- Непрерывность функции
- Точки разрыва
- Операции над непрерывными функциями
- Схема исследования функции на непрерывность
- Свойства непрерывных функций на отрезке (a; b)
РАЗРЫВНАЯ ФУНКЦИЯ
— функция 

Р. ф. возникают, напр., при интегрировании по параметру элементарных функций (см. Дирихле разрывный множитель), при вычислении суммы функциональных рядов, членами к-рых являются элементарные функции, в частности при вычислении суммы тригонометрич. рядов, в задачах оптимального управления.

Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Смотреть что такое «РАЗРЫВНАЯ ФУНКЦИЯ» в других словарях:
РАЗРЫВНАЯ ФУНКЦИЯ — функция, имеющая разрыв в некоторых точках (см. Разрыва точка). У функций, встречающихся в применениях математики, точки разрыва обычно изолированы, но существуют функции, для которых все точки являются точками разрыва … Большой Энциклопедический словарь
разрывная функция — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN discontinuous function … Справочник технического переводчика
разрывная функция — функция, имеющая разрыв в некоторых точках (см. Разрыва точка). У функций, встречающихся в применениях математики, точки разрыва обычно изолированы, но существуют функции, для которых все точки являются точками разрыва. * * * РАЗРЫВНАЯ ФУНКЦИЯ… … Энциклопедический словарь
РАЗРЫВНАЯ ФУНКЦИЯ — функция, имеющая разрыв в нек рых точках (см. Разрыва точка). У функций, встречающихся в применениях математики, точки разрыва обычно изолированы, но существуют функции, для к рых все точки являются точками разрыва … Естествознание. Энциклопедический словарь
разрывная функция скорости — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN noncontinuous velocity functionabruptly changing velocity … Справочник технического переводчика
РАЗРЫВНАЯ ВАРИАЦИОННАЯ ЗАДАЧА — задача вариационного исчисления, в к рой экстремум функционала достигается на ломаной экстремали. Л о м ан а я э к с т р е м а л ь кусочно гладкое решение Эйлера уравнения, удовлетворяющее в угловых точках нек рым дополнительным необходимым… … Математическая энциклопедия
ВЫПУКЛАЯ ФУНКЦИЯ — действительного переменного функция , определенная на нек ром интервале, для любых двух точек х 1 и x2 к рого выполняется условие Геометрически это означает, что середина любой хорды графика функции f лежит либо над графиком, либо на нем. Если… … Математическая энциклопедия
разрыва точка — значение аргумента, при котором нарушается непрерывность функции. См. Непрерывная функция, Разрывная функция. * * * РАЗРЫВА ТОЧКА РАЗРЫВА ТОЧКА, значение аргумента, при котором нарушается непрерывность функции. См. Непрерывная функция (см.… … Энциклопедический словарь
Бэра классификация — (математика) классификация разрывных функций (См. Разрывные функции). К 1 му классу относится всякая разрывная функция, которая может быть представлена как предел сходящейся в каждой точке последовательности непрерывных функций (функций… … Большая советская энциклопедия
Математическая формула — Эта статья об обозначениях элементарной математики; Для более общего контекста см.: Математические обозначения. Математическая формула (от лат. formula уменьшительное от forma образ, вид) принятая в математике (а также… … Википедия
Источник
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 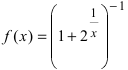
Решение:
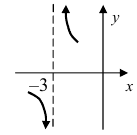
Нарисуем график функции в окрестности нуля (Рис. 64): 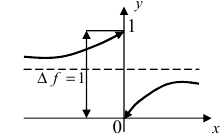
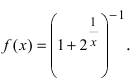
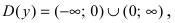
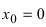
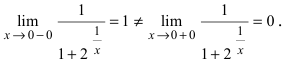
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция 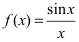
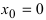
Решение:
В точке 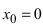
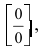
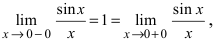
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 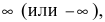
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 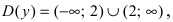
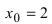
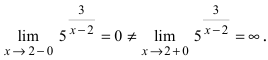
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 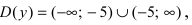
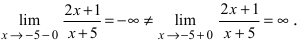
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 
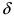
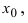
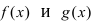
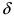
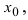
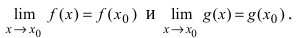
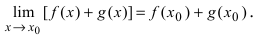
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 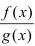
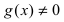
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
- находят область определения функции; точки, в которых функция не определена, являются точками подозрительными на разрыв: если функция задана словесным образом, т.е. описывается разными формулами на разных интервалах, то точками подозрительными на разрыв являются точки, определяющие границы интервалов;
- исследуют подозрительные на разрыв точки, для чего вычисляют лево- и правосторонние пределы; классифицируют точки разрыва;
- при наличии точек разрыва строят график функции в малой
-окрестности точки
.
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
точка
является точкой подозрительной на разрыв.
- вычислим левосторонний
и правосторонний
пределы; так как пределы бесконечные, то точка
является точкой разрыва второго рода;
- построим график функции в небольшой окрестности точки разрыва (Рис. 65).
Рис. 65. Поведение графика функции 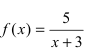
Из рисунка видно, что график функции 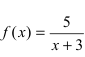
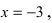
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 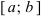
Определение: Замкнутый интервал 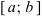
Приведем без доказательства свойства непрерывных функций на сегменте 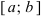
Теорема: Если функция 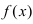
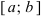
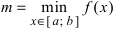
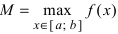
Пример:
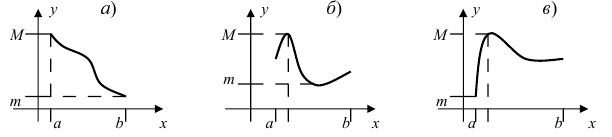
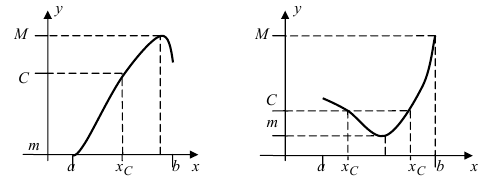
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 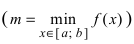
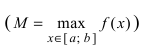
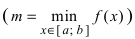
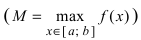
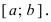
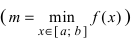
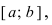
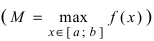
Тб. Если функция 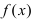
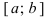
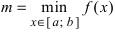
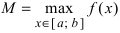
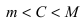
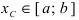
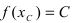
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 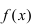
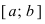
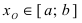
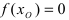
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
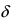 -окрестности;
-окрестности;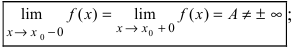
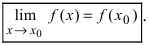
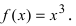
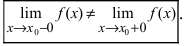
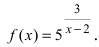
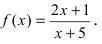
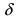 -окрестности точки
-окрестности точки 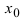 .
.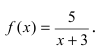
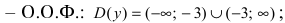 точка
точка 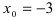 является точкой подозрительной на разрыв.
является точкой подозрительной на разрыв.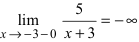 и правосторонний
и правосторонний 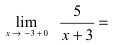
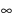 пределы; так как пределы бесконечные, то точка
пределы; так как пределы бесконечные, то точка 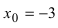 является точкой разрыва второго рода;
является точкой разрыва второго рода;