Что значит разность квадратов чисел

Квадрат суммы и разности

Квадрат суммы

Выражение (a + b) 2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b) 2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 + 2ab + b 2 называется разложением квадрата суммы.

Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.

Пример. Возвести в квадрат выражение 3x 2 + 2xy.

Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:

Квадрат разности

Выражение (a — b) 2 — это квадрат разности чисел a и b. Выражение (a — b) 2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 — 2ab + b 2 называется разложением квадрата разности.

Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трёхчлена:

Решение: Используя формулу квадрата разности, находим:

(2a 2 — 5ab 2 ) 2 = (2a 2 ) 2 — 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 .

Теперь преобразуем выражение в многочлен стандартного вида:

(2a 2 ) 2 — 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 = 4a 4 — 20a 3 b 2 + 25a 2 b 4 .

Разность квадратов

Выражение a 2 — b 2 — это разность квадратов чисел a и b. Выражение a 2 — b 2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.

Пример. Преобразуйте произведение в двучлен:

(5a 2 + 3)(5a 2 — 3) = (5a 2 ) 2 — 3 2 = 25a 4 — 9.

В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:

На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.

Источник

Как использовать разность квадратов a 2 − b 2

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула разности квадратов.

a 2 − b 2 = (a − b)(a + b)

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a + b) = a 2 − b 2

Как разложить на множители разность квадратов

Рассмотрим пример. Необходимо разложить на множители разность квадратов.

Обратим внимание, что « 64y 2 » — это « (8y) 2 », значит, для формулы разности квадратов вместо « a » мы используем « 8y ».

Используем формулу разности квадратов. На месте « a 2 » у нас будет « 64y 2 », а на месте « b 2 » стоит « 36x 2 ».

Разность квадратов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов обратно в разность квадратов, используя формулу сокращенного умножения.

Обратим внимание, что произведение многочленов « (с + 3d)(с − 3d) » напоминает правую часть формулы разности квадратов « a 2 − b 2 = (a − b)(a + b) », только вместо « a » стоит « c », а на месте « b » стоит « 3d ».

Используем для « (с + 3d)(с − 3d) » формулу разности квадратов в обратную сторону.

Рассмотрим другой пример. Требуется упростить произведение многочленов.

Если сравнить « (x 2 + 4y 3 )(x 2 − 4y 3 ) » с правой частью формулы разности квадратов
« a 2 − b 2 = (a − b)(a + b) », то можно понять, что на месте « a » из первой скобки стоит « x 2 , а на месте « b » стоит « 4y 3 ».

Одночлены, которые стоят на месте « a » или « b » как в формуле, могут стоять в степени.

Например, в рассматриваемом примере на месте « a » стоит « x 2 ». Это означает, что именно « x 2 » мы рассматриваем как « a ».

Используем формулу разности квадратов и решим пример до конца.

Рассмотрим пример сложнее. Требуется разложить на множители многочлен, используя формулу разности квадратов.

Представим « (a + 2b) 2 − 9a 2 » как разность квадратов « a 2 − b 2 ».

Одночлены, которые стоят на месте « a » или « b » как в формуле, могут быть в скобках, т.е. быть многочленами.

В рассматриваемом примере на месте « a 2 » стоит многочлен « (a + 2b) 2 ». Это означает, что мы рассматриваем всю скобку « (a + 2b) » как « a » для формулы.

Решим пример до конца. После применения формулы разности квадратов не забудем привести подобные в примере.

Источник

Разность квадратов

Что такое разность квадратов

Разность квадратов двух чисел или выражений равняется сумме этих чисел/выражений, умноженной на их разность. То есть формула представляет собой разложение многочлена на множители:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Доказательство формулы разности квадратов

Арифметическое доказательство

Чтобы подтвердить справедливость определения разности квадратов, рассмотрим правую часть уравнения.

Раскроем скобки и получим:

(a+b)(a−b)=a 2 +ab−ba−b 2 =a 2 −b 2

Справедливость формулы доказана.

Геометрическое доказательство

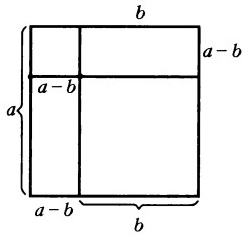
Построим квадрат, сторона которого равна a, отсюда следует, что площадь S=a 2 .

Далее начертим внутри имеющегося правильного четырехугольника квадрат со стороной b, следовательно площадь (S_b) данной фигуры будет равна b 2 .

Продолжим любую прямую, на которой лежит сторона меньшего квадрата, до пересечения со стороной большего четырехугольника. В результате внутри исходного квадрата со стороной a имеем:

• квадрат со стороной b;
• прямоугольник, стороны которого равны а и (a−b);
• прямоугольник со сторонами b и (a−b).

Теперь найдем величину, которая останется при вычитание площади меньшего квадрата из площади большего. Как видим по чертежу, она равна площадям двух образовавшихся прямоугольников, то есть:

Применение формулы разности квадратов

Формула разности квадратов в алгебре может использоваться в двух видах случаев:

• при раскрытии скобок;
• при упрощении выражений.

Примеры прямого использования формулы и формулировка стандартной ошибки

Необходимо раскрыть скобки в выражении:

Возьмем 15m в качестве a, 12n — в качестве b, значит:

Исходя из формулы, запишем:

Подставим в полученное выражение исходные переменные:

Стандартная ошибка прямого использования формулы заключается в следующем. Если в исходном выражении переместить в начало множитель со знаком плюс, при этом поменяв местами слагаемые, то получим:

В данном варианте записи зачастую происходит путаница с уменьшаемым и вычитаемым, то есть:

Следует обратить внимание на множитель со знаком минус.

Возьмем 8f за a, 4e за b, тогда:

Учитывая возможность совершения стандартной ошибки при использовании формулы сокращенного умножения (разности квадратов), обращаем внимание на второй множитель, выраженный разностью. Чтобы применить формулу, нам необходимо поменять местами слагаемые в первом множителе. Тогда получим:

Выполним подстановку исходных переменных:

Видим, что числитель раскладывается на множители по формуле разности квадратов:

Источник

Разность квадратов: формулы

Что такое разность квадратов

Разность квадратов двух чисел или выражений равняется сумме этих чисел/выражений, умноженной на их разность. То есть формула представляет собой разложение многочлена на множители:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Доказательство формулы разности квадратов

Арифметическое доказательство

Чтобы подтвердить справедливость определения разности квадратов, рассмотрим правую часть уравнения.

Раскроем скобки и получим:

(a+b)(a−b)=a 2 +ab−ba−b 2 =a 2 −b 2

Справедливость формулы доказана.

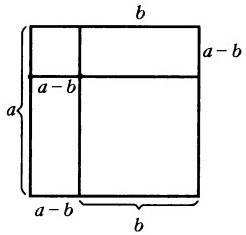
Геометрическое доказательство

Построим квадрат, сторона которого равна a, отсюда следует, что площадь \(S=a^2\) .

Далее начертим внутри имеющегося правильного четырехугольника квадрат со стороной b, следовательно площадь (S_b) данной фигуры будет равна b 2 .

Продолжим любую прямую, на которой лежит сторона меньшего квадрата, до пересечения со стороной большего четырехугольника. В результате внутри исходного квадрата со стороной a имеем:

• квадрат со стороной b;
• прямоугольник, стороны которого равны а и (a−b);
• прямоугольник со сторонами b и (a−b).

Теперь найдем величину, которая останется при вычитание площади меньшего квадрата из площади большего. Как видим по чертежу, она равна площадям двух образовавшихся прямоугольников, то есть:

Применение формулы разности квадратов

Формула разности квадратов в алгебре может использоваться в двух видах случаев:

• при раскрытии скобок;
• при упрощении выражений.

Примеры прямого использования формулы и формулировка стандартной ошибки

Необходимо раскрыть скобки в выражении: \(\left(15m-12n\right)\left(15m+12n\right)\)

Возьмем \(15m\) в качестве \(a\) , \(12n\) — в качестве \(b\) , значит:

Исходя из формулы, запишем:

Подставим в полученное выражение исходные переменные:

Стандартная ошибка прямого использования формулы заключается в следующем. Если в исходном выражении переместить в начало множитель со знаком плюс, при этом поменяв местами слагаемые, то получим:

В данном варианте записи зачастую происходит путаница с уменьшаемым и вычитаемым, то есть:

Следует обратить внимание на множитель со знаком минус.

Раскройте скобки: \(\left(4e+8f\right)\left(8f-4e\right)\)

Возьмем \(8f\) за \(a\) , \(4e\) за \(b\) , тогда:

Учитывая возможность совершения стандартной ошибки при использовании формулы сокращенного умножения (разности квадратов), обращаем внимание на второй множитель, выраженный разностью. Чтобы применить формулу, нам необходимо поменять местами слагаемые в первом множителе. Тогда получим:

Выполним подстановку исходных переменных:

Видим, что числитель раскладывается на множители по формуле разности квадратов:

Источник

Сокращенное умножение: правила, формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

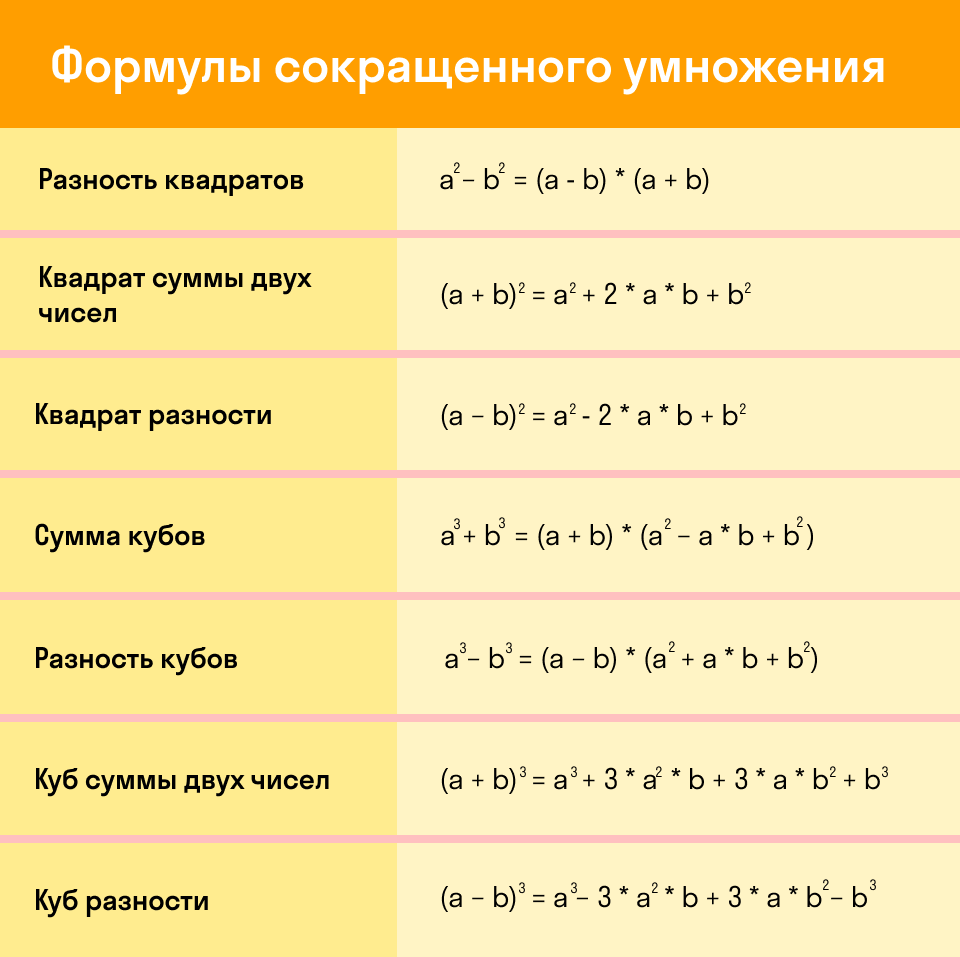
Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

1. Разность квадратов двух выражений равна произведению их разности и их суммы.
2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .

Докажем, что a 2 — b 2 = (a — b) * (a + b).

Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

a 2 — b 2 = a 2 — b 2 + ab — ab

1. Сгруппируем иначе: a 2 — b 2 + a * b — a * b = a 2 — a * b + a * b — b 2
2. Продолжим группировать: a 2 — a * b — b 2 +a * b = (a 2 — a * b) + (a * b — b 2 )
3. Вынесем общие множители за скобки:

   (a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)

1. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
2. Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
3. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10) 2 .

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

1. Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
2. Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник