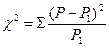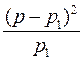Что значит различия недостоверны

Оценка достоверности различия сравниваемых групп по критерию соответствия (хи-квадрат).

При определении характера связи между изучаемыми факторами или явлениями одна из важнейших задач математической статистики заключается в оценке достоверности полученных результатов. Достоверность различий можно оценить по t-критерию, но этот критерий характеризует различия только между двумя совокупностями. При сравнении трех и более совокупностей оценка достоверности при помощи t-критерия затруднительна, так как попарное сравнение не позволяет дать общей оценки различий. Кроме того, сравниваемые группы могут иметь не два результата (да, нет), а несколько. Для решения этой задачи используется критерий «хи-квадрат», разработанный К. Пирсоном. Он же называется коэффициентом согласия и коэффициентом соответствия, «хи-критерием». Он служит для оценки различий в нескольких сравниваемых группах и при нескольких результатах с определенной степенью достоверности (например: оценка различий в распределении детей по частоте заболеваний в районах с разными уровнями загрязнения атмосферного воздуха); определения связи между двумя факторами (результат и зависимый признак). Например, имеется ли связь между жилищными условиями, материальным обеспечением семьи и т. д. и частотой заболеваний, госпитализацией; связь между состоянием физического развития и тяжестью отдельных заболеваний и т. д.; определения идентичности распределения частот двух и более вариационных рядов (коэффициент согласия). Например, одинаково ли распределение частот (детей) по содержанию гемоглобина, количеству эритроцитов, белков крови в двух совокупностях (живущих в зоне загрязнения и «чистой» зоне).

Из приведенных примеров видно, что «хи-квадрат» используется для анализа данных, характеризующих распределение, а не средние величины. Исходный материал для вычислений дается в абсолютных числах по наблюдениям в группах.

Сущность метода «хи-квадрат» заключается в определении достоверности различий между фактическими и теоретическими («ожидаемыми») данными, полученными при условии, что сравниваемые совокупности одинаковы по своему распределению («нулевая гипотеза»). После определения «нулевой гипотезы» на основании этого предположения определяются «ожидаемые» данные, которые сопоставляются с фактическими. Если различий между фактическими и теоретическими числами нет, то нулевая гипотеза подтвердилась и действительно различий в сравниваемых группах нет. Если фактические данные будут отличаться от теоретических, полученных при условии отсутствия различий в распределении, то сравниваемые группы имеют разное распределение и результаты в этих группах статистически достоверно различны.

Таким образом, если Р— фактические данные, P₁ — теоретически исчисленные при нулевой гипотезе, то критерий может быть выражен формулой:

Оценка величины χ 2 проводится по специальной таблице. Различия считаются достоверными. в том случае, когда величина хи-квадрат соответствует вероятности, меньшей 5% (0,05). Это вероятность подтверждения нулевой гипотезы, т. е. предположения, что различия в сравниваемых группах отсутствуют (связи между факторами нет).

Рассмотрим технику вычисления критерия на примере распределения детей по частоте заболеваний в трех зонах проживания.

Фактические данные (р) представлены в таблице

Распределение детей трех районов по частоте заболеваний

Район проживания	Всего детей	Не болели	Эпизодически болели	Часто болели
Зона химического ком­бината Контрольный район № 1 Контрольный район № 2
Всего . . .

1. Определяем рабочую (нулевую) гипотезу. Предполагается, что в любом месте проживания распределение детей по частоте заболевания будет одинаково. Это распределение вычисляется по итоговой строчке (нулевая гипотеза).

Всего детей	Не болели	Эпизодически болели	Часто болели
100%	6,7	46,0	47,3

2. В соответствии с нулевой гипотезой вычисляются новые «ожидаемые» данные. Если бы распределение детей по частоте заболевания было бы одинаковым во всех зонах проживания, то число не болевших, эпизодически и часто болевших детей в первой, второй и третьей зонах было бы следующим:

В зоне химического комбината	В первом контрольном районе
Всего 390 детей	410детей
Не болели 6,7 – 100	6,7 – 100
х – 390	х – 410
Эпизодически болели 46 – 100	46 – 100
х – 390	х – 410
Часто болели 47,3 – 100	47,3 – 100
х – 390	х – 410

«Ожидаемые» результаты (теоретические числа)

Район проживания	«Ожидаемые» числа р,	Разница фактических и «ожидаемых» чисел р – р1
не бо­лели	эпизоди­чески болели	часто болели	не бо­лели	эпизоди­чески болели	часто болели
Зона химического комбината Контрольный рай­он № 1 Контрольный рай­он № 2	– 13 +3 + 10	–96 +55 +40	+ 109 –58 –50

3. Вычисляется разница фактических и «ожидаемых» чисел, представленная в таблице. Так, при нулевой гипотезе мы ожидали, что в зоне химического комбината число не болевших детей составит 26, эпизодически болевших 179, часто болевших 185. Фактически они составили соответственно: 13, 83, 294.

Различия фактических и «ожидаемых» чисел обусловлены несовпадением нулевой гипотезы и фактического состояния.

4. Различия возводят в квадрат.

5. Вычисляют различия на единицу ожидаемых наблюдений, т. е. квадрат разницы делят на число «ожидаемых» единиц:

Зоны проживания	(р – р1) 2	(р – р1) 2
р1
Не болели	Эпизодически болели	Часто болели	Не болели	Эпизодически болели	Часто болели
Зона химического комбината	6,5	51,5	64,2
Контрольный рай­он № 1	0,3	16,1	17,3
Контрольный рай­он № 2	8,7	8,7	13,2

Суммируют результаты последнего этапа — расчета: 6,5 + 0,3 + 3,7 + 51,5 + 16,8 и т. д. Сумма составляет—181,5. Это и есть критерий соответствия (χ 2 ).

6. Оценку величины χ 2 производим по таблице.

Вероятность подтверждения нулевой гипотезы (хи-квадрат)
n’	0,05=5%	0,01=1 %	0,002=0,2%	n’	0,05=5 %	0,01=1%	0,002=0,2 %
I	3,8	6,6	9,5	21,0	26,2	31,0
6,0	9,2	12,4	22,4	27,7	32,5
7,8	11,3	14,8	23,7	29,1	34,0
9,5	13,3	16,9	25,0	30,6	35,5
11,1	15,1	18,9	26,3	32,0	37,0
12,6	16,8	20,7	27,6	33,4	38,5
14,1	18,5	22,6	28,9	34,8	40,0
15,5	20,1	24,3	30,1	36,2	41,5
16,9	21,7	26,1	31,4	37,6	43,0
18,3	23,2	27,7	32,7	38,9	44,5
19,7	24,7	29,4	33,9	40,3	46,0

В первой колонке по вертикали обозначены числа степеней свободы, числа самой таблицы представляют различные величины χ 2 , вверху таблицы даны вероятности подтверждения нулевой гипотезы.

Оценим полученный результат в нашем примере.

Число степеней свободы определяется по формуле:

где: S — число сравниваемых групп (строк), r — число групп (граф) результатов.

В нашем исследовании S (число групп детей, проживающих в различных районах загрязнения воздуха) — 3, r (число рассматриваемых параметров их здоровья) — 3 (не болели, эпизодически болели, часто болели),

В четвертой строке таблицы ищем значение χ 2 , соответствующее полученному результату 181,5. Он больше 16,9, значит вероятность нулевой гипотезы в нашем примере менее 0,2%. Правила оценки таковы, что различия считаются достоверными в сравниваемых группах, а также подтверждается наличие связи между результатом и влияющим фактором, если нулевая гипотеза подтверждается с вероятностью меньшей чем 5% (Р 0,05), то различия считаются недостоверными и связь отсутствующей.

В нашем примере вероятность нулевой гипотезы менее 0,2%, отсюда связь между загрязнением атмосферного воздуха и частотой заболеваний детей имеется и она доказывается с достаточно большой надежностью.

Источник

Уровень статистической значимости (р)

В таблицах результатов статистических расчётов в курсовых, дипломных и магистерских работах по психологии всегда присутствует показатель «р».

Например, в соответствии с задачами исследования были рассчитаны различия уровня осмысленности жизни у мальчиков и девочек подросткового возраста.

Уровень статистической значимости (p)

Мальчики (20 чел.)

Локус контроля — «Я»

Локус контроля — «Жизнь»

* — различия статистически достоверны (р≤0,05)

В правом столбце указано значение «р» и именно по его величине можно определить значимы различия осмысленности жизни в будущем у мальчиков и девочек или не значимы. Правило простое:

• Если уровень статистической значимости «р» меньше либо равен 0,05, то делаем вывод, что различия значимы. В приведенной таблице различия между мальчиками и девочками значимы в отношении показателя «Цели» — осмысленность жизни в будущем. У девочек этот показатель статистически значимо выше, чем у мальчиков.
• Если уровень статистической значимости «р» больше 0,05, то делается заключение, что различия не значимы. В приведенной таблице различия между мальчиками и девочками не значимы по всем остальным показателям, за исключением первого.

Откуда берется уровень статистической значимости «р»

Уровень статистической значимости вычисляется статистической программой вместе с расчётом статистического критерия. В этих программах можно также задать критическую границу уровня статистической значимости и соответствующие показатели будут выделяться программой.

Например, в программе STATISTICA при расчете корреляций можно установить границу «р», например, 0,05 и все статистически значимые взаимосвязи будут выделены красным цветом.

Если расчёт статистического критерия проводится вручную, то уровень значимости «р» выявляется путем сравнения значения полученного критерия с критическим значением.

Что показывает уровень статистической значимости «р»

Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи, например, между агрессивностью и тревожностью.

То есть, коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?

Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.

Какой уровень статистической значимости лучше: 0,01 или 0,05

Уровень статистической значимости отражает вероятность ошибки. Следовательно, результат при р=0,01 более точный, чем при р=0,05.

В психологических исследованиях приняты два допустимых уровня статистической значимости результатов:

р=0,01 – высокая достоверность результата сравнительного анализа или анализа взаимосвязей;

р=0,05 – достаточная точность.

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать

Источник

Оценка достоверности отличий

Оценка часто необходима при сравнительном анализе полярных групп. Эти группы можно выделить, учитывая различную выраженность определенного целевого признака (характеристики) изучаемого явления. Обычно анализ начинают с подсчета первичных статистик выделенных групп, затем оценивают достоверность отличий. Очень часто количественный анализ одним сравнением не ограничивается, появляется необходимость провести дополнительные сопоставления и выявить новые свидетельства. Выбор новых критериев наугад — дело неблагодарное. Лучше для этого использовать результаты корреляционного анализа.

Например, если вы исследуете личностную обусловленность желания принимать участие в экологическом движении, то признаком, по которому могут быть выделены полярные группы, могут выступить субъективные оценки испытуемых, экспертные оценки, некоторые поведенческие индикаторы, представленные в числовой форме. Если показатели интеллектуального развития имеют небольшую величину коэффициента корреляции (

Одной из наиболее часто встречающихся задач при обработке данных является оценка достоверности отличий между двумя, или более, рядами значений. В математической статистике существует ряд способов для этого. Для использования большинства мощных критериев требуются дополнительные вычисления, обычно весьма развернутые.

Компьютерный вариант обработки данных стал в настоящее время наиболее распространенным. Во многих прикладных статистических программах есть процедуры оценки различий между параметрами одной выборки или разных выборок. При полностью компьютеризованной обработке материала нетрудно в нужный момент использовать соответствующую процедуру и оценить интересующие различия. Однако большинство психологов не имеют свободного и неограниченного доступа к работе с компьютером — либо недостаточен парк ЭВМ, либо психолог как пользователь ЭВМ не подготовлен и может проводить обработку только с помощью квалифицированного персонала. И в том, и в другом случае типичный сеанс работы с компьютером заканчивается тем, что психолог получает принтерные распечатки, содержащие подсчитанные первичные статистики, результаты корреляционного анализа, иногда и факторного (компонентного).

Основной анализ осуществляется позже, не в диалоге с ЭВМ. Исходя из этих рассуждений, будем считать, что перед психологом часто встает задача оценки достоверности различий с использованием ранее вычисленных статистик. При сравнении средних значений признака говорят о достоверности (недостоверности) отличий средних арифметических, а при сравнении изменчивости показателей — о достоверности (недостоверности) отклонений сигм (дисперсии) и коэффициентов вариации.

Достоверность различий средних арифметических можно оценить по достаточно эффективному параметрическому критерию Стьюдента. Он вычисляется по формуле

m1 + m2

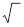
где M1 и M2 — значения сравниваемых средних арифметических, m1 и m2 — соответствующие величины статистических ошибок средних арифметических. Знак вычисленной разности средних арифметических можно не учитывать, поскольку имеет значение только абсолютная величина критерия t.

Значения критерия Стьюдента t для трех уровней значимости (p) приведены в приложении 2. Число степеней свободы определяется по формуле d = n + n — 2, где n и n — объемы сравниваемых выборок. С уменьшением объемов выборок (n

Пример. M1 =113.3, m1 =2.4, n =13; M2 =103.3, m2 =2.6, n =16.

2.4 + 2.6

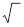
для d=13+16-2=27 вычисленная величина превышает табличную для вероятности Р=0.01. Вычисленное значение 2.83 больше табличного 2.77 для уровня значимости Р=0.01. Следовательно, различия между средними достоверны на уровне 0.01.

Приведенная формула проста. Используя ее, можно с помощью бытового калькулятора с памятью вычислить t критерий без промежуточных записей.

Следует помнить, что при любом численном значении критерия достоверности различия между средними этот показатель оценивает не степень выявленного различия (она оценивается по самой разности между средними), а лишь статистическую достоверность его, т.е. право распространять полученный на основе сопоставления выборок вывод о наличии разницы на все явление (весь процесс) в целом. Низкий вычисленный критерий различия не может служить доказательством отсутствия различия между двумя признаками (явлениями), ибо его значимость (степень вероятности) зависит не только от величины средних, но и от численности сравниваемых выборок. Он говорит не об отсутствии различия, а о том, что при данной величине выборок оно статистически недостоверно: слишком велик шанс, что разница при данных условиях определения случайна, слишком мала вероятность ее достоверности.

Степень, т.е. величину выявленного различия, желательно оценивать, опираясь на содержательные критерии. Вместе с тем, для психологического исследования весьма характерно наличие множества показателей, которые, по существу, являются условными баллами, и валидность оценивания с помощью них следует доказывать особо. Чтобы избежать большей произвольности, в таких случаях также приходится опираться на статистические параметры.

Пожалуй, наиболее распространено для этого использование сигмы. Разницу между двумя средними арифметическими в одну сигму и более можно считать достаточно выраженной. Если сигма подсчитана для ряда значений более 35, то достаточно выраженным можно считать различие 0.5 сигмы. Однако для ответственных выводов о том, насколько велика разница между значениями, лучше использовать строгие критерии.

Источник