- Что значит равновесная система
- Равновесные и неравновесные состояния
- Понятие термодинамического равновесия. Равновесные и неравновесные системы.
- Химическое равновесие. Принцип Ле Шателье
- Понятие химического равновесия
- Признаки химического равновесия
- Принцип Ле Шателье
- Влияние температуры на химическое равновесие
- Влияние давления на химическое равновесие
- Влияние концентрации на химическое равновесие
- Константа химического равновесия
- Примеры решения задач
- Задачи для самостоятельного решения
Что значит равновесная система
Термодинамически равновесное состояние тела или системы это такое состояние теплового и механического равновесия элементов тела или системы, которое без внешнего воздействия может сохраняться сколь угодно долго.
Равновесная система это система тел, находящихся в термодинамическом равновесии, в противном случае она будет называться неравновесной системой.
Так, без учета гравитационных сил, равновесное состояние тела или системы есть такое их состояние, при котором по всему их объему давления и температуры имеют одинаковые значения. Равенство только давления во всех точках обусловливает механическое равновесие, равенство температур — термическое равновесие.
При неравновесном состоянии тела (системы) в разных его частях могут быть различны и температуры и давления. Однако в неравновесной системе могут быть точки, в которых некоторые термические параметры одинаковы. Геометрическое место точек в пространсве, занимаемом системой (телом), с одинаковыми температурами представляет собой изотермическую поверхность, а с одинаковым давлением — изобарическую поверхность. Такие поверхности называются изопотенциальными. Изопотенциальные поверхности не могут пересекаться. Изопотенциальные поверхности могут быть и при равновесном состоянии тела. Например, в высоком цилиндре с жидкостью на различных уровнях от его дна будут различные изобарные поверхности, обусловленные дейсвием гравитационного поля земли. Поэтому равенство параметров в равновесной системе делается с оговоркой — без учета гравитационных сил.
Все термодинамические параметры гомогенной сисемы (однородной — с одинаковыми физическими свойствами), находящейся в равновесном состоянии, имеют определенную функциональную связь. При отсутствии действия внешних полей, термодинамически равновесное состояние любого однородного реального тела определяется всего лишь двумя независимыми параметрами. Для неоднородных систем могут два параметра взаимно определять друг друга (например, давление и температура влажного насыщенного пара), в этом случае необходим третий параметр.
В качестве независимых параметров могут быть выбраны: давление и температура, давление и удельный объём, или любая пара независимых свойств (температура и энтропия, давление и энтальпия, и т.п.). Например, связь между параметрами p, v, T может быть выражена термическими уравнениями состояния системы:
— в неявной форме
 |
— в явной форме
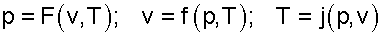 | CO | O2 | CO2 |
| Сисходн, моль/л | 0,52 | 0,48 | 0 |
| Спрореагир,моль/л | 0,32 | 0,16 | 0,16 |
| Сравн, моль/л | 0,2 | 0,32 | 0,16 |
Во второй строке под Спрореагир понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO2, причем, Сисходн= Спрореагир + Сравн.
Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса
Решение.
ΔG298 о = 2·(- 16,71) кДж = -33,42·10 3 Дж.
lnK = 33,42·10 3 /(8,314× 298) = 13,489. K = 7,21× 10 5 .
Задача 3. Определите равновесную концентрацию HI в системе
если при некоторой температуре константа равновесия равна 4, а исходные концентрации H2 , I2 и HI равны, соответственно, 1, 2 и 0 моль/л.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л H2.
| Вещество | H2 | I2 | HI |
| сисходн., моль/л | 1 | 2 | 0 |
| спрореагир., моль/л | x | x | 2x |
| cравн., моль/л | 1-x | 2-x | 2x |
Тогда, К = (2х) 2 /((1-х)(2-х))
Решая это уравнение, получаем x = 0,67.
Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.
Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H2(г) + HCOH(г) →CH3OH(г) становится равной 1. Принять, что ΔН о Т » ΔН о 298, а ΔS о T » ΔS о 298.
Решение.
Если К = 1, то ΔG о T = — RTlnK = 0;
ΔН о 298 = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10 3 Дж;
ΔS о 298 = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;
0 = — 86100 — Т·(-109,52)
Задача 5. Для реакции SO2(Г) + Cl2(Г) →SO2Cl2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO2Cl2, если исходные концентрации SO2, Cl2 и SO2Cl2 равны 2, 2 и 1 моль/л соответственно.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO2.
| Вещество | SO2 | Cl2 | SO2Cl2 |
| cисходн., моль/л | 2 | 2 | 1 |
| cпрореагир., моль/л | x | x | х |
| cравн., моль/л | 2-x | 2-x | x + 1 |
Решая это уравнение, находим: x1 = 3 и x2 = 1,25. Но x1 = 3 не удовлетворяет условию задачи.
Следовательно, [SO2Cl2] = 1,25 + 1 = 2,25 моль/л.
Задачи для самостоятельного решения
1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.
Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества
газообразных веществ, то равновесие сместится вправо в реакции 3.
2. При некоторой температуре равновесные концентрации в системе:
составляли: [HBr] = 0,3 моль/л, [H2] = 0,6 моль/л, [Br2] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.
К = 4; исходная концентрация HBr составляет 1,5 моль/л.
3. Для реакции H2(г) + S(г) →H2S(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H2 и S, если исходные концентрации H2, S и H2S равны, соответственно, 2, 3 и 0 моль/л.
[H2] = 0,5 моль/л; [S] = 1,5 моль/л.
4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса
становится равной 1. Примите, что ΔН о Т≈ΔН о 298, а ΔS о T≈ΔS о 298
5. Используя справочные данные, рассчитайте константу равновесия процесса:
6. Для реакции 2С3Н8(г) → н-С5Н12(г)+СН4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.
7. При температуре 500 К константа равновесия процесса:
равна 3,4·10 -5 . Вычислите Δ G о 500.
8. При температуре 800 К константа равновесия процесса н-С6Н14(г)+ 2С3Н6(г)+Н2(г) равна 8,71. Определите ΔG о f,800(С3Н6(г)), если ΔG о f,800(н-С6Н14(г)) = 305,77 кДж/моль.
9. Для реакции СО(г) + Cl2(г) →СO2Cl2(г) при некоторой температуре равновесная концентрация СO2Cl2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО(г) и Cl2(г) равны соответственно 2,0 и 1,8 моль/л.
10. При некоторой температуре равновесные концентрации в системе 2SО2(г) + О2(г) →2SO3(г) составляли: [SО2 ]=0,10 моль/л, [О2]=0,16 моль/л, [SО3]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО2 и О2.
К=4,0; исходная концентрация SО2 составляет 0,18 моль/л;
исходная концентрация О2 составляет 0,20 моль/л.
Источник



