Что значит равноугольная проекция

НАВИГАЦИЯ. Глава 3. §19 Классификация картографических проекций.

§19 Классификация картографических проекций.

Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт, наиболее употребительными признаками их классификации служат:

• характер искажений проекций, обусловливающий возможности практического использования карт;

• вид меридианов и параллелей нормальной сетки.

По характеру искажений

все картографические проекции делятся на четыре группы:

• равноугольные, или конформные;

• равновеликие, или эквивалентные (равноплощадные);

Равноугольные проекции

Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли.

Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом.

Однако, при сохранении неискаженными углов и направлений, в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.

Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.

Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.

К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.

Равновеликие проекции

Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте.

Бесконечно малый на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.

На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.

Равнопромежуточные проекции

Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений.

Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга.

Произвольные проекции

Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.

К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.

По виду меридианов и параллелей нормальной картографической сетки

проекции делятся на следующие основные группы:

Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.

Конические проекции

Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов.

Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса.

Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.

Азимутальные проекции

Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов

Из приведенного определения видно, что азимутальные проекции являются частным случаем конических проекций.

Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Свойствами азимутальных проекций являются: равноугольность, равновеликость или равнопромежуточность.

К классу азимутальных проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки.

Эта точка называется точкой зрения.

Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.

В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:

— на ортографические, когда точка зрения удалена в бесконечность;

— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;

— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т.е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);

— на центральные (гномонические), когда точка зрения помещена в центре глобуса.

Цилиндрические проекции

Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми.

Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.

Общие уравнения цилиндрических проекций имеют вид:

x = f (φ); y = C λ

Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр. При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т.е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр линиями нулевых искажений будут являться параллели сечения.

Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.

Источник

Справка

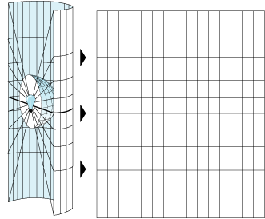
Независимо от того, представляете ли вы Землю в виде сферы или сфероида , ее трехмерную поверхность необходимо преобразовать в плоский лист карты. Это преобразование, выполняемое по математическим законам, называется картографической проекцией. Одним из простых способов понимания того, как картографические проекции изменяют пространственные свойства, является визуализация проекции света сквозь Землю на поверхность, которая называется проекционной поверхностью. Представьте чистую поверхность Земли с нанесенной на нее градусной сеткой . Оберните кусок бумаги вокруг Земли. Источник света в центре Земли отбросит тени от сетки координат на кусок бумаги. Вы можете теперь развернуть бумагу и положить ее на плоскость. Форма координатной сетки на плоской поверхности бумаги очень отличается от ее формы на поверхности Земли. Картографическая проекция исказила градусную сетку.

Спроецировать сфероид на плоскость нисколько не легче, чем разложить на ней кусок апельсиновой кожуры – он будет разорван. При отображении Земной поверхности в двухмерном пространстве искажается форма, площадь, длина или направление объектов.

Картографическая проекция использует математические формулы для связи сферических координат на глобусе с плоскими координатами.

Различные проекции имеют разные типы искажений. Некоторые проекции разработаны с учетом минимизации искажений одной или двух характеристик данных. Проекция может сохранять площадь пространственного объекта, но изменять его форму. На рисунке ниже объекты вблизи полюсов вытянуты.

На схеме ниже показаны трехмерные пространственные объекты, сжатые для их отображения на плоской поверхности.

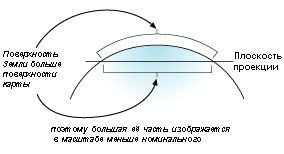
Картографические проекции предназначены для определенных целей. Одна картографическая проекция может использоваться для данных большого масштаба в ограниченной области, а другая – для карт мира маленького масштаба. Картографические проекции, используемые для мелкомасштабных карт, обычно основаны на сферических, а не сфероидальных географических системах координат.

Равноугольные проекции

Равноугольные проекции сохраняют без искажений малые локальные формы. Для сохранения отдельных углов, описывающих пространственные отношения, равноугольная проекция должна также представлять линии картографической сетки пересекающимися под углом 90° на карте. Это достигается с помощью сохранения всех углов. Недостаток заключается в том, что площадь, ограниченная рядом кривых, может быть в процессе преобразования значительно искажена. Все картографические проекции искажают форму больших объектов на земной поверхности.

Равновеликие проекции

Равновеликие проекции сохраняют площадь изображаемых объектов. Это достигается за счет искажения других свойств, таких как форма, углы и масштаб. В равновеликих проекциях параллели и меридианы могут не пересекаться под правильными углами. В некоторых случаях, особенно на картах небольших территорий, искажение форм не является очевидным, и очень трудно отличить равноугольную проекцию от равновеликой, если только она не была соответствующим образом определена по документации или путем измерений.

Равнопромежуточные проекции

Карты в равнопромежуточных проекциях сохраняют расстояния между определенными точками. Правильный масштаб не сохраняется никакой проекцией на всей карте, однако, в большинстве случаев существует одна или более линий на карте, вдоль которых масштаб сохраняется постоянным. В большинстве равнопромежуточных проекций есть одна или несколько линий, длина которых на карте равна (в масштабе карты) длине соотносимой с нею линии на глобусе, независимо от того, является ли эта линия большой или малой окружностью, прямой или кривой линией. О таких расстояниях говорят, что они истинные. Например, в Синусоидальной проекции экватор и все параллели имеют свою истинную длину. В других равнопромежуточных проекциях могут быть истинными экватор и все меридианы. Иные проекции (например, равнопромежуточная проекция двух точек) показывают истинный масштаб между одной или двумя точками и каждой другой точкой на карте. Необходимо иметь в виду, что ни одна проекция не бывает равнопромежуточной по отношению ко всем точкам на карте.

Азимутальные проекции (истинного направления)

Кратчайший путь между двумя точками на сферической поверхности, такой как поверхность Земли, пролегает вдоль сферического эквивалента прямой линии на плоской поверхности. Это большая окружность, на которой лежат две точки. Проекции истинного направления, или азимутальные проекции, используются для сохранения некоторых кривых, описывающих большие окружности, и придают правильные азимутальные направления всем точкам на карте относительно центра. Некоторые проекции этого типа являются также равноугольными, равновеликими или равнопромежуточными.

Источник

ArcMap

Независимо от того, представляете ли вы Землю в виде сферы или сфероида , ее трехмерную поверхность необходимо преобразовать в плоский лист карты. Это преобразование, выполняемое по математическим законам, называется картографической проекцией. Одним из простых способов понимания того, как картографические проекции изменяют пространственные свойства, является визуализация проекции света сквозь Землю на поверхность, которая называется проекционной поверхностью. Представьте чистую поверхность Земли с нанесенной на нее градусной сеткой . Оберните кусок бумаги вокруг Земли. Источник света в центре Земли отбросит тени от сетки координат на кусок бумаги. Вы можете теперь развернуть бумагу и положить ее на плоскость. Форма координатной сетки на плоской поверхности бумаги очень отличается от ее формы на поверхности Земли. Картографическая проекция исказила градусную сетку.

Спроецировать сфероид на плоскость нисколько не легче, чем разложить на ней кусок апельсиновой кожуры – он будет разорван. При отображении Земной поверхности в двухмерном пространстве искажается форма, площадь, длина или направление объектов.

Картографическая проекция использует математические формулы для связи сферических координат на глобусе с плоскими координатами.

Различные проекции имеют разные типы искажений. Некоторые проекции разработаны с учетом минимизации искажений одной или двух характеристик данных. Проекция может сохранять площадь пространственного объекта, но изменять его форму. На рисунке ниже объекты вблизи полюсов вытянуты.

На схеме ниже показаны трехмерные пространственные объекты, сжатые для их отображения на плоской поверхности.

Картографические проекции предназначены для определенных целей. Одна картографическая проекция может использоваться для данных большого масштаба в ограниченной области, а другая – для карт мира маленького масштаба. Картографические проекции, используемые для мелкомасштабных карт, обычно основаны на сферических, а не сфероидальных географических системах координат.

Равноугольные проекции

Равноугольные проекции сохраняют без искажений малые локальные формы. Для сохранения отдельных углов, описывающих пространственные отношения, равноугольная проекция должна также представлять линии картографической сетки пересекающимися под углом 90° на карте. Это достигается с помощью сохранения всех углов. Недостаток заключается в том, что площадь, ограниченная рядом кривых, может быть в процессе преобразования значительно искажена. Все картографические проекции искажают форму больших объектов на земной поверхности.

Равновеликие проекции

Равновеликие проекции сохраняют площадь изображаемых объектов. Это достигается за счет искажения других свойств, таких как форма, углы и масштаб. В равновеликих проекциях параллели и меридианы могут не пересекаться под правильными углами. В некоторых случаях, особенно на картах небольших территорий, искажение форм не является очевидным, и очень трудно отличить равноугольную проекцию от равновеликой, если только она не была соответствующим образом определена по документации или путем измерений.

Равнопромежуточные проекции

Карты в равнопромежуточных проекциях сохраняют расстояния между определенными точками. Правильный масштаб не сохраняется никакой проекцией на всей карте, однако, в большинстве случаев существует одна или более линий на карте, вдоль которых масштаб сохраняется постоянным. В большинстве равнопромежуточных проекций есть одна или несколько линий, длина которых на карте равна (в масштабе карты) длине соотносимой с нею линии на глобусе, независимо от того, является ли эта линия большой или малой окружностью, прямой или кривой линией. О таких расстояниях говорят, что они истинные. Например, в Синусоидальной проекции экватор и все параллели имеют свою истинную длину. В других равнопромежуточных проекциях могут быть истинными экватор и все меридианы. Иные проекции (например, равнопромежуточная проекция двух точек) показывают истинный масштаб между одной или двумя точками и каждой другой точкой на карте. Необходимо иметь в виду, что ни одна проекция не бывает равнопромежуточной по отношению ко всем точкам на карте.

Азимутальные проекции (истинного направления)

Кратчайший путь между двумя точками на сферической поверхности, такой как поверхность Земли, пролегает вдоль сферического эквивалента прямой линии на плоской поверхности. Это большая окружность, на которой лежат две точки. Проекции истинного направления, или азимутальные проекции, используются для сохранения некоторых кривых, описывающих большие окружности, и придают правильные азимутальные направления всем точкам на карте относительно центра. Некоторые проекции этого типа являются также равноугольными, равновеликими или равнопромежуточными.

Источник