Что значит равносильные предложения

Задача 4. Доказать, что уравнения 3х (х — 2) = 0 и 3х(х — 2)(х + 3) = 0 равносильны на множестве целых неотрицательных чисел.

Решение. Множество решений первого уравнения –Т₁= <0, 2>, множество решений второго, заданного на множестве целых неотри­цательных чисел, Т₂ = <0, 2>. Число -3 (см. задачу 3) множеству Т₂, не принадлежит, потому что оно не является целым неотрицательным. Имеем, что Т₁ = Т₂, следовательно, данные уравнения на множестве целых неотрицательных чисел равносильны.

Заметим, что мы рассматриваем понятия логического следования и равносильности для одноместных высказывательных форм. Для предложений, содержащих две и более переменных, эти понятия определяются аналогично.

Отметим также, что знак Û использовался раньше, в частности, при рассмотрении логической структуру явных определений понятий. Было установлено, что ее можно представить в виде а Û в. Употребление знака Û здесь не случайно. Дело в том, что определение, как говорят в математике, порождает два равносильных предложения, которые затем используются наряду с другими в доказательствах. Например, определение «квадратом называется прямоугольник, имеющий равные соседние стороны» порождает равносильные предложения: «если прямоугольник является квадратом, то в нем соседние стороны равны» и «если в прямоугольнике соседние стороны равны, то прямоугольник является квадратом». Использовать в доказательствах можно любое из этих двух.

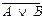
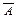
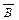
Знак Ûтакже использовался в записи правил построения отрицания высказываний. Например, Û Ú ; . В этом случае речь идет о равносильности высказываний определенной формы. При этом считают, что предложения равносильны, если они одновременно истинны, либо одновременно ложны. Другими словами, если их значения истинности совпадают при одинаковых наборах значений высказываний А и В.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Значение слова «равносильный»

2. Равный по значению, по значительности, производящий то же действие или вызывающий те же последствия; равнозначный. Мы первые скажем, что употреблять иностранное слово, когда есть равносильное ему русское слово, — значит оскорблять и здравый смысл и здравый вкус. Белинский, Взгляд на русскую литературу 1847 г. Нет ничего оскорбительнее для честного бойца, чем предложение врага сдаться. Такое предложение равносильно для моряка удару плетью по лицу. Новиков-Прибой, Боевые традиции русских моряков.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

РАВНОСИ’ЛЬНЫЙ, ая, ое; -лен, льна, льно (книжн.). 1. Равной силы. Равносильные борцы. 2. Обладающий таким же значением, производящий то же действие или вызывающий те же последствия, как кто-н. другой, что-н. другое, тожественный. Событие, равносильное катастрофе.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

равноси́льный

1. одинаковый, равный с другим, другими по силе, мощи

2. совершенно подобный, равный по значению, значимости другому, другим; тождественный

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова летаргический (прилагательное):

Источник

Тема: Равносильность предложений

Урок 68

Тема: «Равносильность предложений»

1) сформировать представление о равносильных высказываниях, умение в простейших случаях устанавливать отношения равносильности и его записывать с помощью знака «Û»;

2) повторить и закрепить виды высказываний, понятие темы и ремы, признаки делимости, разностное и кратное сравнение, решение уравнений, теоретико-множественные представления и символику.

1) задания для актуализации знаний:

423; 408; 393; 378; .

«9 делитель числа 423», «423 делится на 9».

а) Число 333 имеет три простых делителя.

б) Число 333 имеет шест делителей.

в) Число 333 делится на 3.

г) Число 333 делится на 3 и на 37.

д) Число 3 является делителем 333.

е) Число 333 кратно 3.

ж) Число 333 можно представить в виде произведения 3k (k N).

з) Число 333 – составное.

1. Определить, из каких слов состоит новое понятие.

2. Подобрать синонимы к понятию.

3. Сформулировать признаки равносильных утверждений.

4. Подобрать знак, которым можно заменить слово «равносильность».

5. Приведите один не математический и один математический пример равносильный утверждений.

6. Выполнить пробное задание.

3) понятие равносильных утверждений:

Два предложения, означающие одно и то же, называют равносильными утверждениями.

4) знак равносильности:

Для обозначения равносильных предложений используют знак равносильности: Û

5) чтение знака равносильности:

. в том, и только том случае.

6) образец выполнения задания в парах:

2) 34 + 18 : b = 43 Û 18 : b = 43 – 34 Û 18 : b = 9 Û b = 18 : 9 Û b = 2

7) подробный образец для самопроверки самостоятельной работы:

7) Истинно; 8) истинно.

1) 2а – 3 = 25 Û 2а = 25 + 3 Û 2а = 28 Û а = 28 : 2 Û а = 14.

1) карточка для рефлексии деятельности:

Я знаю, что означает «равносильные утверждения»

Я могу определить, являются ли утверждения равносильные

Я знаю, с помощью какого знака записываются равносильные утверждения

Я знаю, как можно перевести на русский язык утверждения, записанные с помощью знака равносильности

Я знаю новый способ записи решения уравнений

Я могу, используя знак равносильности при решении уравнений

Ход урока

1. Мотивация к учебной деятельности

1) включение учащихся в учебную деятельность;

2) организовать деятельность учащихся по установке тематических рамок: высказывания;

3) создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.

Организация учебного процесса на этапе 1:

– На прошлом уроке вы проанализировали свои знания по теме «Простые числа и делимость».

— Что показали результаты контрольной работы? (Результаты показали, что мы можем идти дальше.)

— При изучении прошлых тем вы строили новые понятия, доказывали общие утверждения, использовали математическую символику для записи определений, свойств, признаков на математическом языке, на предстоящих уроках вы более глубоко рассмотрите правила, которые позволяют грамотно формулировать разные утверждения. На уроках, как всегда будет много открытий, как вы будете делать открытия?

— С чего начнёте работу?

2. Актуализация знаний и фиксация затруднения в пробном учебном действии.

1) организовать актуализацию изученных способов действий, достаточных для построения нового знания:

2) зафиксировать актуализированные способы действий в речи;

3) зафиксировать актуализированные способы действий в знаках (эталоны);

4) организовать обобщение актуализированных способов действий;

5) организовать актуализацию мыслительных операций, достаточных для построения нового

знания: анализ, сравнение, обобщение;

6) мотивировать к выполнению пробного действия;

7) организовать самостоятельное выполнение пробного учебного действия;

8) организовать фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия или в его обосновании.

Организация учебного процесса на этапе 2:

– Цифра сотен трехзначного числа – 4, цифра единиц – 3. Зная, что это число кратно 9, определите его цифру десятков. (423.)

– Как иначе можно сказать о том, что число 423 кратно 9? (9 делитель числа 423, число 423 делится на 9.)

На доске: «9 делитель числа 423», «423 делится на 9» (Д-1).

— Можно сказать, что данные вами формулировки означают одно и то же?

На доске карточка с числами: 423; 408; 393; 378; . (Д-1)

— Установите закономерность и продолжите ряд на три числа. (423; 408; 393; 378; 363; 348; 333.)

– Что интересного вы заметили? (Все числа делятся на 3, числа стоят в порядке убывания.)

— Как вы определили, что числа делятся на 3?

— Сформулируйте признак делимости на 3.

— Из чего состоит сформулированное утверждение?

На доске карточка с признаком делимости на 3.

– Какие простые числа входят в разложение числа 333 на простые множители? (Две тройки и число 37.)

— Как по-другому можно сформулировать, что числа 3 и 37 простые делители числа 333? (Число 333 кратно своим простым делителям 3 и 37.)

— Что, явилось основанием вашего вывода, что числа 3 и 37 простые? (Понятие простого числа.)

— Будет ли означать одно и тоже, что «числа простые» и «числа имеют только два делителя»?

— Что вы сейчас повторили?

— А теперь я для вас приготовила пробное задание, что вам надо будет с ним сделать? (Надо будет определить, что в задании нового и попробовать его выполнить.)

На доске карточка с утверждениями (Д-1):

а) Число 333 имеет три простых делителя.

б) Число 333 имеет шест делителей.

в) Число 333 делится на 3.

г) Число 333 делится на 3 и на 37.

д) Число 3 является делителем 333.

е) Число 333 кратно 3.

ж) Число 333 можно представить в виде произведения 3k (k N).

з) Число 333 – составное.

– Подчеркните равносильные предложения.

— Чем это задание отличается от предыдущих заданий? (В предыдущих заданиях надо было определить или сформулировать утверждения означающие одно и то же, а теперь надо найти равносильные утверждения.)

— У кого нет ответа?

— Сформулируйте своё затруднение. (Мы не смогли определить, какие утверждения являются равносильными.)

— Какие получили результаты?

Варианты учащихся (буквенный код) записываются на доске или выставляются планшетки с ответами на доску.

— Что вы видите? (Ответы у всех разные.)

— Кто может доказать (обосновать, предъявить эталон), какой ответ правильный и все ли равносильные утверждения перечислены?

— Сформулируйте своё затруднение. (Мы не можем доказать, чей ответ правильный, все ли равносильные утверждения выписаны.)

— Что вы будете делать дальше?

3. Выявление места и причины затруднения

1) организовать восстановление выполненных операций;

2) организовать фиксацию места (шага, операции), где возникло затруднение;

3) организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т. д.);

4) на этой основе организовать выявление и фиксацию во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.

Организация учебного процесса на этапе 3:

– Какое задание вы должны были выполнить? (Мы должны были выписать равносильные утверждения.)

— Как вы действовали, выполняя задание?

— Где у вас возникло затруднение? (В понимании того, что такое равносильные утверждения.)

– Почему задание вызвало затруднение? (Мы не знаем, какими признаками обладают равносильные утверждения, что такое равносильные утверждения.)

— Что дальше вы будете делать?

4. Построение проекта выхода из затруднения

организовать построение проекта выхода из затруднения:

— учащиеся ставят цель проекта (целью всегда является устранение причины возникшего затруднения);

— учащиеся уточняют и согласовывают тему урока;

— учащиеся определяют средства (алгоритмы, модели, справочники и т. д.);

— учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.

Организация учебного процесса на этапе 4:

– Сформулируйте цель вашей деятельности. (Определить, какими признаками обладают равносильные утверждения, что такое равносильные утверждения.)

– Сформулируйте тему урока. (Равносильные утверждения.)

— Что вы можете использовать, чтобы узнать новое понятие? (Можно использовать учебник.)

— А можно определить новое понятие через словообразование этого понятия?

— Сегодня вы попробуете поработать со словом, определяющим новое понятие.

— Как вы будете работать? (Проанализируем из каких слов состоит слово, соответствующее новому понятию, выявим признаки, по которым можно определить равносильность утверждений, выясним, каким знаком можно заменить слово равносильность.)

5. Реализация построенного проекта

1) организовать реализацию построенного проекта в соответствии с планом;

2) организовать фиксацию нового способа действия в речи;

3) организовать фиксацию нового способа действия в знаках (с помощью эталона);

4) организовать фиксацию преодоления затруднения;

5) организовать уточнение общего характера нового знания (возможность применения нового способа действий для решения всех заданий данного типа).

Организация учебного процесса на этапе 5:

— Сегодня вы будете работать в группах. Определите, из каких слов состоит новое понятие, подберите синонимы к понятию, сформулируйте признаки равносильных утверждений, подберите знак, которым можно заменить слово «равносильность», приведите один не математический и один математический пример равносильный утверждений, выполните пробное задание.

План фиксируется на доске (Д-2).

Группы работают 3 минуты. Одна из групп представляет свою версию выполнения задания, остальные работают на дополнение и уточнение.

После согласования на доску вывешиваются эталоны (Д-3, Д-4, Д-5).

— Где можно проверить сделанные вами выводы? (В учебнике.)

– Откройте учебники на стр. 160, каждая группа читает п. 1.

— Где можно использовать понятие и знак равносильности утверждений?

— Что теперь необходимо сделать?

6. Первичное закрепление во внешней речи

организовать усвоение детьми нового способа действий при решении данного класса задач с их проговариванием во внешней речи: фронтально.

Организация учебного процесса на этапе 6:

Задание выполняется устно.

г) 12 делится на 2, но 2 не делится на 12;

д) 10 + 2 делится на 12, но 10 не делится на 12;

е) 10 × 2 делится на 20, 10 не делится ан 20;

ж) 32 – 1 = 8, но 3 + 2 не равно 7;

з) 4 4, 4 – 3 не меньше 1.

Задание выполняется устно.

1) Л; 2) И; 3) Л; 4) И; 5) Л; 6) И.

Задание выполнятся у доски.

(80 – с) : 8 = 7 Û 80 – с = 7 × 8 Û 80 – с = 56 Û с = 80 – 56 Û с = 24.

Задание выполнить в парах, с проверкой по образцу (Д-6). Ошибки анализируются, исправляются.

— Какой следующий шаг необходимо сделать?

7. Самостоятельная работа с самопроверкой по эталону

1) организовать самостоятельное выполнение учащимися типовых заданий на новый способ действия;

2) организовать соотнесение работы с эталоном для самопроверки (в случае, когда учащиеся начинают осваивать процедуру грамотного самоконтроля возможно соотнесение работы с подробным образцом);

3) организовать вербальное сопоставление работы с эталоном для самопроверки*

(в случае, когда способ действия состоит из нескольких шагов – организация пошаговой проверки);

4) по результатам выполнения самостоятельной работы организовать рефлексию деятельности по применению нового способа действия.

* В случае, когда учащиеся начинают осваивать процедуру грамотного самоконтроля возможно вербальное сопоставление работы с подробным образцом.

Организация учебного процесса на этапе 7:

— Для самостоятельной работы я вам предлагаю выполнить №№ 813 (7, 8);

Учащиеся работают самостоятельно. Сопоставляю свои работы с подробным образцом (Д-7).

— Как вы определяли верность утверждений в первом задании?

— Где у вас возникло затруднение?

— Почему возникло затруднение?

— Чем вы воспользовались при выполнении второго задания?

— Где возникло затруднение?

— Почему у вас возникло затруднение во втором задании?

— У кого оба задания выполнено правильно?

— Какой вывод вы можете сделать?

8. Включение в систему знаний и повторение.

1) тренировать навыки использования нового содержания совместно с ранее изученным материалом: запись утверждений на математическом языке, равносильных данным утверждениям на русском языке;

2) повторить и закрепить: перевод с русского языка на математический язык; понятие темы и ремы.

Организация учебного процесса на этапе 8:

Задание выполняется у доски.

Задание выполняется устно, фронтально.

Перед началом выполнения задания повторить, что такое тема и рема.

а) Растения, имеющие корни – деревья. Нет.

б) Всякое чётное число делится на 2. Да.

в) Всякое натуральное число, делящееся на 5, оканчивается на 5. Нет.

г) Дробь большая или равная 1, является неправильной. Да.

9. Рефлексия деятельности на уроке

1) организовать фиксацию нового содержания, изученного на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;

3) организовать оценивание учащимися собственной деятельности на уроке;

4) организовать фиксацию неразрешённых затруднений на уроке как направлений будущей учебной деятельности;

5) организовать обсуждение и запись домашнего задания.

Организация учебного процесса на этапе 9:

– Какое понятие вы сегодня определили? (Равносильность утверждений.)

— Что вы узнали о равносильных утверждениях?

— Что вы использовали при выходе из затруднения?

– Проанализируйте свою деятельность на уроке и дайте своей работе оценку.

Учащиеся работают с карточками для рефлексии (Р-1).

п.2.5.1.; эталоны; №№ 818 (два уравнения на выбор); 819.

Источник