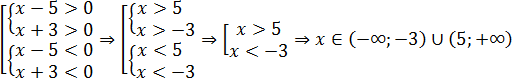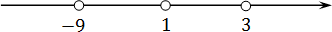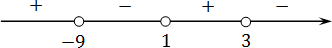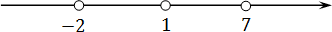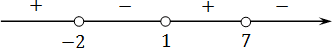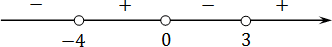Что значит равно трем интервалам

Метод интервалов: решение простейших строгих неравенств

Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:

Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 x + 3

Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:

x 2 − 2 x − 15 > 0

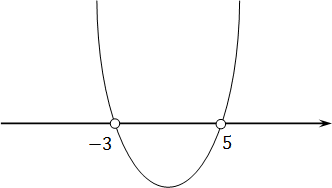
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:

Функция больше нуля там, где она проходит выше оси OX . В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.

Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.

Почему эти методы неэффективны?

Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.

Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:

( x − 7)( x − 1)( x + 4)( x + 9) f ( x ) > 0 и f ( x ) f ( x ) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;

Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;

Выяснить знак (плюс или минус) функции f ( x ) на самом правом интервале. Для этого достаточно подставить в f ( x ) любое число, которое будет правее всех отмеченных корней;

Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.

Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f ( x ) > 0, или знаком «−», если неравенство имеет вид f ( x ) x − 2)( x + 7) x − 2)( x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.

Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:

Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:

f ( x ) = ( x − 2)( x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;

Получаем, что f (3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.

Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.

Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:

Вернемся к исходному неравенству, которое имело вид:

( x − 2)( x + 7) x + 9)( x − 3)(1 − x ) x + 9)( x − 3)(1 − x ) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.

Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.

Шаг 2: отмечаем все корни на координатной прямой:

Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:

f ( x ) = ( x + 9)( x − 3)(1 − x );
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197

Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:

( x + 9)( x − 3)(1 − x ) f ( x ) x ∈ (−9; 1) ∪ (3; +∞)

Это и есть ответ.

Замечание по поводу знаков функции

Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.

Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:

1. Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f ( x ) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
2. Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.

Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.

Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.

Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид ( a ; +∞), где a — самый большой корень уравнения f ( x ) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:

( x − 1)(2 + x )(7 − x ) f ( x ) = ( x − 1)(2 + x )(7 − x );
( x − 1)(2 + x )(7 − x ) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.

Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:

Требуется найти знак функции f ( x ) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.

«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f ( x ) = −1 и f ( x ) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.

На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:

f ( x ) = ( x − 1)(2 + x )(7 − x )

Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.

Первая скобка: ( x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x ). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x ). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.

Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:

Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:

Исходное неравенство имело вид:

( x − 1)(2 + x )(7 − x ) x ∈ (−2; 1) ∪ (7; +∞)

Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:

Заменяем неравенство уравнением и решаем его:

x (2 x + 8)( x − 3) = 0;
x = 0;
2 x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

Отмечаем все три корня на координатной прямой (сразу со знаками):

Справа на координатной оси стоит плюс, т.к. функция имеет вид:

f ( x ) = x (2 x + 8)( x − 3)

А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:

Источник

Что значит 3 интервала в ворде?

Как сделать три межстрочных интервала?

Чтобы изменить межстрочный интервал в текстовом редакторе word, выделите нужный текстовой фрагмент и перейдите на вкладку “Главная”, где в группе “Абзац”, воспользуйтесь инструментом “Интервал”. На экран будет выведен список с часто используемыми значениями интервала, но только в сторону его увеличения.

Как сделать в ворде 3 интервала?

Как изменить междустрочный интервал в Word

1. На вкладке Конструктор нажмите кнопку Интервал между абзацами.
2. Наведите указатель на каждый вариант для предварительного просмотра, а затем выберите подходящий. Чтобы настроить одинарный интервал, выберите пункт Интервал между абзацами отсутствует.

Чему равен 1 межстрочный интервал?

Интервалы между строками и знаками». Одинарный межстрочный интервал равен 4,233 мм (1/6 дюйма); шаг письма – 2,54 мм (1/10 дюйма). ГОСТ Р 7.0.97-2016 устанавливает, что при составлении документов может использоваться межстрочный пробел (интервал) от 1 до 1,5.

Что значит тройной интервал?

Тройной — двум строкам. Таким образом, если весь текст набирается полуторным интервалом и в некоторых местах должен быть тройной интервал, можно просто вставить пустую строку. В сумме как раз получится тройной интервал.

Как сделать 2 интервала в ворде?

Двойной пробел во всем документе

1. На вкладке Главная в группе Стили щелкните правой кнопкой мыши обычный ивыберите изменить.
2. В области Форматированиенажмите кнопку Двойной пробел и нажмите кнопку ОК. Форматирование всего документа изменяется на двойной интервал.

Сколько ПТ в одном интервале?

Одинарный интервал примерно равен высоте прописной буквы выбранного шрифта. Так для шрифта 14 размера междустрочный одинарный интервал составит чуть более 14 пунктов.

Как сделать межстрочный интервал 1.5 в ворде?

Для этого необходимо выделить текст и нажать на небольшую кнопку справа от надписи «Абзац» на вкладке «Главная». После этого откроется окно с настройками отступов и интервалов. Здесь необходимо открыть выпадающее меню в разделе «Интервал» и выбрать вариант «1.5 строки».

Как в ворде сделать интервал между абзацами?

Изменение междустрочных интервалов для части документа

1. Выделите абзацы, которые нужно изменить.
2. На домашней >между строками и абзацем.
3. Выберите нужное количество междустрок или выберите «Другие варианты междустрок», а затем за выберите нужные параметры в области «Интервал».

Как в ворде сделать абзацный отступ?

Отступ в Word 2003

1. Выделяем форматируемый текст, правой кнопкой мыши выбираем из списка «Абзац», в разделе «Отступы» задаем необходимый интервал в поле «Первая строка». …
2. Также можно регулировать отступы бегунком вверху страницы, который вызывается вкладкой «Вид» — разделом «Линейка».

Как поставить межстрочный интервал одинарный?

Применение одинарного интервала к части документа

1. Выделите абзацы, которые нужно изменить.
2. Перейдите на главная > междустрок и интервалов между .
3. Выберите значение 1,0.

Что такое межстрочный интервал?

Интерлинья́ж (от фр. interligne, буквально — написанное между строк) — междустрочный пробел, расстояние между базовыми линиями соседних строк. В компьютерной вёрстке это понятие обычно называют «межстрочный интервал» (англ. line spacing).

Как понять межстрочный интервал?

2 ответа У ворда межстрочный интервал — это расстояние между строками в абзаце. Измеряется от нижней линии предыдущей строки до верхней черты следующего (по высоте строчных букв). Одинарным называется интервал, равный высоте кегля.

Какой должен быть интервал между абзацами?

междустрочный интервал — 1,5 строки, безо всяких отступов «до» и «после» абзацный отступ должен быть одинаковым на протяжении всего текста и равняться 1,25 см

Как убрать большой пробел между абзацами в ворде?

Если Вам нужно просто удалить лишний абзац на странице в Ворде, выделите его мышкой – для этого достаточно кликнуть по нему три раза левой кнопкой мыши. Затем нажмите кнопку «Delete» или «Backspace» на клавиатуре.

Сколько пунктов в полуторном интервале?

Полуторный интервал соответствует расстоянию между соседними строками в 1,5 раза больше, чем при выборе одинарного интервала. Например, если используется полуторный интерлиньяж при размере символов 10 пт., то расстояние между строками равно примерно 15 пт.

Источник