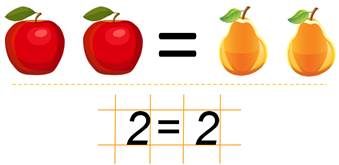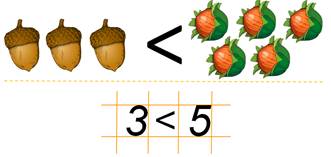- Знаки: «>» больше, « —> В данный момент вы не можете посмотреть или раздать видеоурок ученикам Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге. Получите невероятные возможности Конспект урока «Знаки: «>» больше, « Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать. — Ежик, ну что ты там видишь? — О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать. — Ой. Ко второму пню, ну там где крошки, сорока наша прилетела. — Так где птиц больше? — На пне с зернышками птиц больше, чем около пня с крошками. — Белочка, кажется дядя Филя прилетел. — Ну, и где сейчас птиц стало больше? — Теперь птиц стало одинаково. — Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно. Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум. Теперь мы сравним грибы: три боровика и две лисички. Что больше? — Три боровика больше, чем две лисички. — Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два. — А сейчас сравним жёлуди и орехи. Чего меньше? — Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов. — Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три. А теперь мы посмотрим, как пишутся эти знаки. — Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот. — Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так. В знаке меньше палочки сходятся к меньшему числу и записывается он так. — Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки. — Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше. А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше. Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства. Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства. Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага… что-то не так, три обозначает большее количество предметов, чем четыре и при счете идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем. — А давай лучше исправим, чтобы у нас не было ошибок. — Давай. Значит здесь надо поставить знак меньше. Вот. — Так-так. Пять равно пяти. Все верно. — Ага, а здесь совсем сложно. — Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один. — А сколько будет два да три. — Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше. — Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить: 1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно. 2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство. 3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство. 4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством. — Белочка, а давай посмотрим, что там наши птицы делают? — Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось. — Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки. Источник Как пишется знак больше и знак меньше Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно. Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни. Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее? Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко. Содержание: Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже. А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее. Как и в какую сторону пишется знак больше В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей. Пример использования знака больше: 50>10 — число 50 больше числа 10; посещаемость студента в этом семестре составила >90% занятий. Как и в какую сторону пишется знак меньше Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше. Пример использования знака меньше: 100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее. На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше. Знак больше или равно на клавиатуре Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим. Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста. Знак меньше или равно на клавиатуре Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим. Или просто скопируйте его с этой страницы, если вам так будет проще, вот он. Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто. Источник Репетитор по математике о методике использования стрелок Почему отстающие ученики считают математику одним из самых трудных и неподъемных предметов, (если не самой сложной из наук вообще)? Любой разбирающийся в проблемах обучения репетитор по математике ответит Вам следующее: главная сложность в овладении математикой состоит в необходимости работать с большими объемами информации, уводящими в бесконечность. И все многообразие используемых данных, операций и их результатов приходится пос держать в голове. К сожалению, физиологические возможности человека могут не соответствовать заданному уровню. Как и любой другой преподаватель по любой другой дисциплине, репетитор по математике учит обрабатывать предоставленную по условию задачи информацию. Для этого, как минимум, нужно уметь проводить преобразования в удобном для их оформления и проверке виде. Каждый более-менее сносный репетитор по математике использует в своей системе работы классические формы и стандарты, придерживаясь определенного порядка их появления в тетради или на доске. От того, насколько компактно и полно репетитор по математике представит информацию визуальным рядом, зависит удобство ее обработки головным мозгом ученика и, как следствие, степень усвоения изучаемого правила. В математике очень многое строится на подстановках, соответствиях, заменах, сравнениях и т.д. Один и тот же объект, одна и та же величина, может иметь не одну форму записи и часто случается так, что репетитор по математике записывает в тетрадь одну из них, а при решении задач использует другую. При таком переходе внимание ученика не успевает “засечь” мысль репетитора и происходит мгновенное отключение школьника из процесса. Виной всему физиологические особенности переключения внимания. Пока ребенок сообразит, откуда и куда попало в равенство то или иное выражение или число, репетитор по математике уйдет в рассуждениях далеко вперед. Это нельзя допускать. Я, например, предпочту лишний раз сделать круг, и два три раза повторить (показать) одно и то же, чем галопом лететь вперед. Однако, такая тактика репетитора по математике не очень эффективна, ибо репетитор теряет в скорости движения по задачам, а, следовательно, в количестве решенного (отработанного) на уроке. Поэтому выигрывает тот репетитор по математике, кто умеет соединять разрозненные характеристики в единой целое. Нужен некий инструмент, единая форма для всех ситуаций, с помощью которой репетитор по математике сможет быстрее и точнее акцентировать внимание ученика на важных свойствах объекта, на проводимых “трансформациях”. Настоящей палочкой-выручалочкой для репетитора служит схематический подход к визуальному оформлению. Схемы позволяют репетитору по математике использовать минимум словесных описаний при объяснениях и максимально объемно представлять информацию, ее перемещение. В математике много стандартных общепризнанных условных обозначений, но репетитор может водить свои «фишечки». Для того чтобы не возникало недопонимания со стороны ученика, репетитор по математике заранее договаривается с ним о назначении того или иного знака. Одной из разновидностей такого приема является методика стрелочек . Как и когда репетитор по математике использует стрелки? Стрелка указывают на любые объекты, если нужно соотнести их с какой-либо ценной информацией. Очень часто я использую стрелки для демонстрации объекта, вставляемого в выписанное равенство. Именно в таком виде используется большинство формул. Берется какое-нибудь равенство и в его переменные подставляются буквенные или числовые выражения. Например, репетитор по математике выписывает теорему косинусов в общем виде, а затем вместо обозначений участвующих в ней сторон вставляет соответствующие им числа (или буквенные выражения). Далее само равенство подскажет ученику необходимое действие. Или будет вычисляться последний параметр или составится уравнение. Репетитор по математике показывает такую вставку стрелками: Какие стрелки применяются репетитором? Стрелки, которыми репетитор по математике упрощает теоретические записи В последнее время я стал использовать схематические записи определений. К сожалению у репетитора не всегда имеется достаточное количество времени на то, чтобы записать с учеником названия составных частей изучаемого объекта. Но даже в отсутствие дефицита времени, не очень хочется нагружать теоретическую тетрадь лишними текстами. Репетитору по математике лучше действовать следующим образом: 1) нарисовать объект; 2) к каждой его составной части, имеющей название, подвести стрелку; 3) Сделать запись у ее начала. Пример: на приведенном ниже рисунке показано, как репетитор по математике указыват элементы равнобедренного треугольника при помощи стрелок: Именно этот рисунок я обычно заношу с учеником в теоретическую тетрадь. Они заменяют слова «следовательно», «тогда», «поэтому» в схематическом оформлении любых логических переходов, например в доказательствах теорем. Такая форма является своего рода математическим стандартом во всем мире. Постановку логических стрелок можно сравнить со строительством дороги, ведущей от начального пункта (имеющегося математического факта) к конечному пункту (к тому, что доказывается). Указатели подстановок репетитора В таком виде я использую стрелки чуть ли не на каждом уроке. Если нужно показать, куда именно вставляется число (или буквенное выражение), полученное по ходу решения задачи, я выделяю вставляемое рамкой и веду от нее стрелку к месту вставки. Указатели в обучении математике помогают подчеркнуть наиболее важные этапы работы с алгоритмами. Например, при записи общей формулы разложения квадратного трехчлена на множители вместо и репетитор по математике вставляет пропуски. К ним подводятся стрелки от расположенных по близости корней. Такая иллюстрация репетитора по математике позволяет школьникам лучше запоминают значение записанных букв в формуле и порядок производимых действий в практическом примере на разложение. Надо просто найти корни квадратного трехчлена и их вставить. Все очень просто. Еще один пример использования стрелок — работа репетитора по математике с уравнением касательной. Математический анализ (10 — 11 класс). Обилие скобок и «иксов нулевых» в его записи мешает слабому школьнику понять каким образом написать конкретное уравнение на практике. Стрелки репетитора по математике укажут ему на совершаемое действие. Это далеко не все примеры использования указателей. Почти в каждой теме можно найти способ облегчить стрелками понимание и запоминание. Репетитор по математике Москва, А.Н. Колпаков Вы очень талантливый репетитор. Таких не встречала Источник
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Знаки: «>» больше, «
- Как пишется знак больше и знак меньше
- Как и в какую сторону пишется знак больше
- Как и в какую сторону пишется знак меньше
- Знак больше или равно на клавиатуре
- Знак меньше или равно на клавиатуре
- Репетитор по математике о методике использования стрелок
- Как и когда репетитор по математике использует стрелки?
- Какие стрелки применяются репетитором?
Знаки: «>» больше, « —>
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Знаки: «>» больше, «
Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.
— Ежик, ну что ты там видишь?
— О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.
— Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.
— Так где птиц больше?
— На пне с зернышками птиц больше, чем около пня с крошками.
— Белочка, кажется дядя Филя прилетел.
— Ну, и где сейчас птиц стало больше?
— Теперь птиц стало одинаково.
— Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.
Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.
Теперь мы сравним грибы: три боровика и две лисички. Что больше?
— Три боровика больше, чем две лисички.
— Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.
— А сейчас сравним жёлуди и орехи. Чего меньше?
— Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.
— Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.
А теперь мы посмотрим, как пишутся эти знаки.
— Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.
— Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.
В знаке меньше палочки сходятся к меньшему числу и записывается он так.
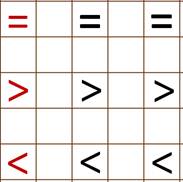
— Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.
— Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.
А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.
Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.
Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.
Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…
что-то не так, три обозначает большее количество предметов, чем четыре и при счете
идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.
— А давай лучше исправим, чтобы у нас не было ошибок.
— Давай. Значит здесь надо поставить знак меньше. Вот.
— Так-так. Пять равно пяти. Все верно.
— Ага, а здесь совсем сложно.
— Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.
— А сколько будет два да три.
— Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.
— Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:
1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.
2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.
3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.
4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.
— Белочка, а давай посмотрим, что там наши птицы делают?
— Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.
— Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.
Источник
Как пишется знак больше и знак меньше

Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше

Пример использования знака меньше:
- 100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
Источник
Репетитор по математике о методике использования стрелок
Почему отстающие ученики считают математику одним из самых трудных и неподъемных предметов, (если не самой сложной из наук вообще)? Любой разбирающийся в проблемах обучения репетитор по математике ответит Вам следующее: главная сложность в овладении математикой состоит в необходимости работать с большими объемами информации, уводящими в бесконечность. И все многообразие используемых данных, операций и их результатов приходится пос держать в голове. К сожалению, физиологические возможности человека могут не соответствовать заданному уровню.
Как и любой другой преподаватель по любой другой дисциплине, репетитор по математике учит обрабатывать предоставленную по условию задачи информацию. Для этого, как минимум, нужно уметь проводить преобразования в удобном для их оформления и проверке виде. Каждый более-менее сносный репетитор по математике использует в своей системе работы классические формы и стандарты, придерживаясь определенного порядка их появления в тетради или на доске. От того, насколько компактно и полно репетитор по математике представит информацию визуальным рядом, зависит удобство ее обработки головным мозгом ученика и, как следствие, степень усвоения изучаемого правила.
В математике очень многое строится на подстановках, соответствиях, заменах, сравнениях и т.д. Один и тот же объект, одна и та же величина, может иметь не одну форму записи и часто случается так, что репетитор по математике записывает в тетрадь одну из них, а при решении задач использует другую. При таком переходе внимание ученика не успевает “засечь” мысль репетитора и происходит мгновенное отключение школьника из процесса. Виной всему физиологические особенности переключения внимания. Пока ребенок сообразит, откуда и куда попало в равенство то или иное выражение или число, репетитор по математике уйдет в рассуждениях далеко вперед. Это нельзя допускать. Я, например, предпочту лишний раз сделать круг, и два три раза повторить (показать) одно и то же, чем галопом лететь вперед.
Однако, такая тактика репетитора по математике не очень эффективна, ибо репетитор теряет в скорости движения по задачам, а, следовательно, в количестве решенного (отработанного) на уроке. Поэтому выигрывает тот репетитор по математике, кто умеет соединять разрозненные характеристики в единой целое. Нужен некий инструмент, единая форма для всех ситуаций, с помощью которой репетитор по математике сможет быстрее и точнее акцентировать внимание ученика на важных свойствах объекта, на проводимых “трансформациях”.
Настоящей палочкой-выручалочкой для репетитора служит схематический подход к визуальному оформлению. Схемы позволяют репетитору по математике использовать минимум словесных описаний при объяснениях и максимально объемно представлять информацию, ее перемещение. В математике много стандартных общепризнанных условных обозначений, но репетитор может водить свои «фишечки». Для того чтобы не возникало недопонимания со стороны ученика, репетитор по математике заранее договаривается с ним о назначении того или иного знака. Одной из разновидностей такого приема является методика стрелочек .
Как и когда репетитор по математике использует стрелки?
Стрелка указывают на любые объекты, если нужно соотнести их с какой-либо ценной информацией. Очень часто я использую стрелки для демонстрации объекта, вставляемого в выписанное равенство. Именно в таком виде используется большинство формул. Берется какое-нибудь равенство и в его переменные подставляются буквенные или числовые выражения. Например, репетитор по математике выписывает теорему косинусов в общем виде, а затем вместо обозначений участвующих в ней сторон вставляет соответствующие им числа (или буквенные выражения). Далее само равенство подскажет ученику необходимое действие. Или будет вычисляться последний параметр или составится уравнение. Репетитор по математике показывает такую вставку стрелками:
Какие стрелки применяются репетитором?
- Стрелки, которыми репетитор по математике упрощает теоретические записи
В последнее время я стал использовать схематические записи определений. К сожалению у репетитора не всегда имеется достаточное количество времени на то, чтобы записать с учеником названия составных частей изучаемого объекта. Но даже в отсутствие дефицита времени, не очень хочется нагружать теоретическую тетрадь лишними текстами. Репетитору по математике лучше действовать следующим образом:
1) нарисовать объект;
2) к каждой его составной части, имеющей название, подвести стрелку;
3) Сделать запись у ее начала.
Пример: на приведенном ниже рисунке показано, как репетитор по математике указыват элементы равнобедренного треугольника при помощи стрелок: 
Именно этот рисунок я обычно заношу с учеником в теоретическую тетрадь.
Они заменяют слова «следовательно», «тогда», «поэтому» в схематическом оформлении любых логических переходов, например в доказательствах теорем. Такая форма является своего рода математическим стандартом во всем мире. Постановку логических стрелок можно сравнить со строительством дороги, ведущей от начального пункта (имеющегося математического факта) к конечному пункту (к тому, что доказывается).
В таком виде я использую стрелки чуть ли не на каждом уроке. Если нужно показать, куда именно вставляется число (или буквенное выражение), полученное по ходу решения задачи, я выделяю вставляемое рамкой и веду от нее стрелку к месту вставки.
Указатели в обучении математике помогают подчеркнуть наиболее важные этапы работы с алгоритмами. Например, при записи общей формулы разложения квадратного трехчлена на множители 



Еще один пример использования стрелок — работа репетитора по математике с уравнением касательной. 

Это далеко не все примеры использования указателей. Почти в каждой теме можно найти способ облегчить стрелками понимание и запоминание.
Репетитор по математике Москва, А.Н. Колпаков
Вы очень талантливый репетитор. Таких не встречала
Источник