Что значит радиус вектора

Радиус-вектор

Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Радиус-вектор в различных системах координат

• Декартовы:

• Полярные, цилиндрические и сферические:

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Радиус-вектор» в других словарях:

РАДИУС-ВЕКТОР — термин, которым в конических сечениях (эллипсе, гиперболе, параболе) называется расстояние какой нибудь точки кривой линии от её фокуса. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. радиус вектор 1) мат. а)… … Словарь иностранных слов русского языка

РАДИУС-ВЕКТОР — произвольной точки пространства вектор, идущий в эту точку из некоторой фиксированной точки (обычно из начала координат) … Большой Энциклопедический словарь

РАДИУС-ВЕКТОР — произвольной точки пространства, вектор, идущий в эту точку из некоторой фиксированной точки (обычно из начала координат) … Энциклопедический словарь

радиус-вектор — радиус вектор, радиуса вектора … Орфографический словарь-справочник

радиус-вектор — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN radius vectorposition vector … Справочник технического переводчика

радиус-вектор — padėties vektorius statusas T sritis fizika atitikmenys: angl. position vector; radius vector vok. Leitstrahl, m; Ortsvektor, m; Radiusvektor, m rus. вектор положения, m; радиус вектор, m pranc. rayon de position, m; rayon vecteur, m; rayon… … Fizikos terminų žodynas

Радиус-вектор — произвольной точки пространства, вектор, идущий в эту точку из некоторой заранее фиксированной точки, называемой полюсом. Если в качестве полюса берётся начало декартовых координат, то проекции Р. в. точки М на оси координат (декартовых… … Большая советская энциклопедия

РАДИУС-ВЕКТОР — точки пространства вектор, идущий в эту точку из нек рой заранее фиксированной точки, называемой п о л ю с о м. Если в качестве полюса берется начало декартовых координат, то проекции Р. в. точки Мна оси координат (декартовых прямоугольных)… … Математическая энциклопедия

РАДИУС-ВЕКТОР — точки вектор, идущий в эту точку из нек рой фиксир. точки, наз. полюсом … Большой энциклопедический политехнический словарь

Источник

Что значит радиус вектора

Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.

Векторная алгебра с нуля!

Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.

Книги по изучению физики и для подготовки к ЕГЭ

Радиус-вектор

Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).

Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.

Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x₁ и y₁ точки В или координаты x₂ и y₂ точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.

Но можно определить положение точки и по-другому, а именно с помощью радиус-вектора. Если известен радиус-вектор данной точки, то и ее положение оказывается известным, поскольку точка конца радиус-вектора совпадает с данной точкой. Так, положение точки В — это конец ее радиус-вектора r₁, а положение точки С — это конец ее радиус-вектора r₂. Этот способ определения положения точки с помощью ее радиус-вектора называется векторным способом.

Эти способы эквивалентны друг другу. Покажем это. Найдем проекции радиус-вектора r₁ точки В на координатные оси. Напомню, чтобы найти проекцию вектора на ось нужно из координаты конца вектора вычесть координату его начала. Тогда

Аналогично для проекций радиус-вектора r₂ точки С:

r_2y = y₂ − 0 = y₂. Таким образом, проекции радиус-векторов точек являются координатами этих точек (рис. 18).

На практике применяются как координатный, так и векторный способы. Более того, при решении многих задач их применяют совместно, что является мощным методом решения, поскольку он позволяет использовать единый подход для решения совершенно разных задач.

Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

© Коллекция подготовительных материалов для успешной сдачи ЕГЭ по физике от Н. Чернова 2012 — 2015 | Контакты: , +79212839427, (81554) 65780

Источник

Координаты вектора в декартовой системе координат (ДСК)

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y ).

Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.

Координатные векторы

Векторы i → и j → называются координатными векторами для заданной системы координат.

Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.

Разложение вектора

Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.

Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = ( 2 ; — 3 ) означает, что вектор a → имеет координаты ( 2 ; — 3 ) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .

Также имеет место быть нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 · i → + 0 · j → .

Равные и противоположные векторы

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Противоположным вектором называется вектор противоположный данному.

Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = ( — a x ; — a y ) .

Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения ( a x ; a y ; a z ) называются координатами вектора в данной (трехмерной) системе координат.

Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ) , j → = ( 0 ; 1 ; 0 ) , k → = ( 0 ; 0 ; 1 ) , координаты нулевого вектора также равны нулю 0 → = ( 0 ; 0 ; 0 ) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = ( — a x ; — a y ; — a z ) .

Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

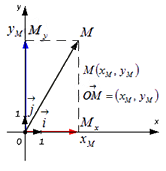
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M ( x M ; y M ) .

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты ( x M ; y M ) в данной системе координат.

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки M ( x M ; y M ; z M ) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = ( x M ; y M ; z M ) .

Источник

10 класс

§ 4. Перемещение. Радиус-вектор

Перемещение.

Шаг, который вы делаете, является примером перемещения. Любое перемещение определяется как его длиной, так и направлением. Величины, которые характеризуются не только числовым значением, но и направлением, называют векторными 1 .

1 Напомним, что величины, которые характеризуются только числовым значением, называют скалярными (скалярами).

Вектором перемещения или просто перемещением называют направленный отрезок прямой, проведённый из начального положения движущегося тела в его конечное положение.

Как и для обычного отрезка, крайние точки вектора часто обозначают буквами. Однако в отличие от обычного отрезка (где А, В — концы отрезка) точка А называется началом вектора, а точка В — его концом. На рисунке 2.5 показан вектор перемещения.

Так же как и обычный отрезок, вектор обладает длиной, которая называется его модулем и обозначается . Модуль вектора так же, как и длину обычного отрезка, можно обозначать одной буквой, например = α. Сам вектор можно записать тоже с помощью одной буквы: .

Радиус-вектор и его проекции.

Положение тела в произвольной точке А пространства (рис. 2.6) можно задать с помощью радиуса вектора.

Радиусом-вектором называют вектор, проведённый из начала системы координат (точки О) в данную точку пространства.

Допустим, что в момент времени t движущееся тело находится в точке А. Длина радиуса- вектора или его модуль | | = r определяет расстояние, на котором точка А (см. рис. 2.6) находится от начала координат. Следовательно, радиус-вектор указывает, на каком расстоянии и в каком направлении находится точка А пространства относительно начала выбранной системы координат.

Проекциями радиуса-вектора = (см. рис. 2.6) на координатные оси X и Y являются координаты конца этого вектора, т. е. точки А. В данном случае r_x и r_y — проекции вектора на оси координат X и У. Тогда r_x = x, r_y = y.

Проекции, как и координаты, могут быть положительными и отрицательными.

Координаты х и y точки А полностью определяют модуль радиуса-вектора и его направление на плоскости относительно координатных осей. Используя теорему Пифагора, запишем:

Проекции вектора перемещения.

Опустив перпендикуляры из начала и конца вектора перемещения (Рис. 2.7) на оси координат X и Y, можно найти его проекции на эти оси. Проекции вектора перемещения — изменения координат 2 Δx и Δy движущегося тела. Изменения координат могут быть как положительными, так и отрицательными величинами, поэтому проекции перемещения на оси координат также могут быть положительными или отрицательными.

2 Изменением любой величины, в том числе координаты, называют разность между значениями величины в конце и начале процесса изменения.

Модуль и направление перемещения полностью определяются его проекциями на оси координат. Модуль перемещения (см. рис. 2.7) можно записать в виде:

Направление вектора определяется углом α: tg α = Δy / Δx. Если, напротив, известен вектор перемещения, то однозначно определяются изменения координат Δx и Δy движущегося тела.

Проекции любой векторной величины находятся так же, как и проекции перемещения. Но они выражаются не в единицах длины, а в тех единицах, в которых выражается модуль данной величины.

Направление вектора (рис. 2.8) можно задать углами α или β между вектором и положительными направлениями осей координат. Из рисунка видно, что модуль проекции α_х равен длине отрезка АС, а модуль проекции α_y — длине отрезка AD. Из прямоугольных треугольников ABC и ABD следует: α_х = αcos α, α_y = αcos β.

Вопросы:

1. Какие величины называют:

2. Что называют вектором перемещения?

3. Что представляют собой проекции радиуса-вектора (см. рис. 2.6)? Как можно определить его модуль?

4. Как можно найти проекции вектора перемещения?

Источник