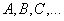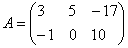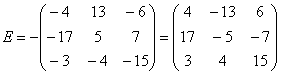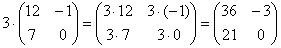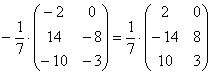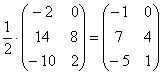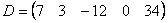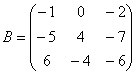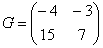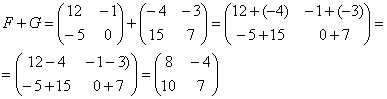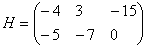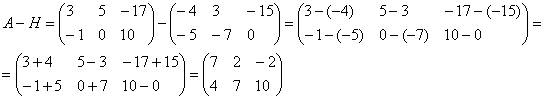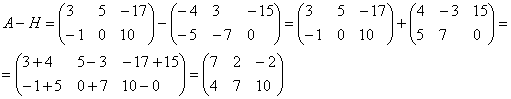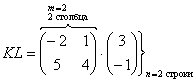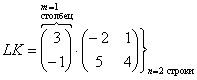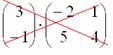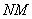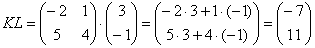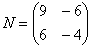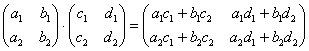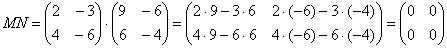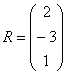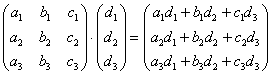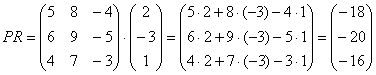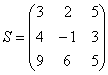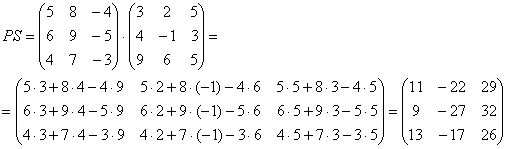- Матричные проекты — заработок или лохоторон
- Что такое матричный проект
- Разновидности
- Матричные проекты можно ли заработать
- Выводы
- Математика для чайников. Матрицы и основные действия над ними
- Определение матрицы
- Операции сложения и вычитания матриц
- Умножение матрицы на число
- Операция умножения матриц
- Операция транспонирования матрицы
- Определитель матрицы
- Действия с матрицами
Матричные проекты — заработок или лохоторон
В последнее время возрастает популярность такого способа заработка в Интернете, как матричные проекты. Что же представляет собой это явление?Матричные проекты — это особая форма многоуровневого или сетевого маркетинга (Multilevel Marketing, или, сокращенно, MLM).
Что такое матричный проект
Точно также как и в других видах MLM, для участника матричного проекта основной задачей является собрать команду и построить структуру. Так же, как и в традиционном МЛМ, доход участника напрямую зависит от построенной структуры. Однако, существует одно принципиальное отличие матричных проектов от классических МЛМ-компаний.
Традиционные МЛМ-компании всегда имеют свой продукт. Это могут быть биоактивные пищевые добавки (БАДы), или косметика и средства личной гигиены, или какое-нибудь программное обеспечение, или информационные продукты (например, тренинги и курсы), или что-либо еще. Матричные же проекты продукта в привычном смысле не имеют. Тот продукт, который они предлагают, продуктом назвать трудно, поскольку продукт этот абсолютно виртуален.
Продуктом, а, вернее, квазипродуктом матричных МЛМ-проектов являются места в матрице, которые оплачивает участник. Оплатив одно место, или несколько мест в матрице (в зависимости от маркетинг-плана проекта), участник получает право продавать приобретенные места тем, кого он пригласил в проект (рефералам).
Если участнику удалось найти рефералов, и они купили у него места в матрице, то он на полученные деньги у того, кто его пригласил (своего спонсора) покупает место в матрице уже следующего уровня и, продает его своим рефералам. Те, в свою очередь, продают купленные уровни уже своим рефералам, и так далее, в зависимости от того, сколько уровней в структуре предусматривает маркетинг-план проекта.
Маркетинг-план того или иного проекта может предусматривать один из трех основных способов построения структуры:
- Матрица с неограниченным количеством мест — то есть, участник проекта может приглашать сколько угодно рефералов (линейная структура)
- Матрица с ограниченным числом мест — под одним спонсором может регистрироваться ограниченное количество рефералов — 2 (бинарная структура), 3, и так далее. Если под участником все места уже заняты, но кто-то регистрируется, пройдя по его партнерской ссылке, то этот человек автоматически переходит либо к спонсору данного участника(«переливы снизу»), либо к одному из его рефералов («переливы сверху»)
- Шахматная матрица — здесь каждый четный, либо нечетный приглашенный автоматически становится рефералом не того, кто его пригласил, а спонсора последнего — таким образом, каждый участник дарит часть рефералов своему спонсору, а сам получает новых рефералов от своих рефералов
Таковы три основных типа структуры, однако, возможны их различные вариации и комбинации.
Разновидности
Нередко матричный проект рассматривают как разновидность финансовой пирамиды. Однако, организаторы матриц, как правило, отрицают свою принадлежность к пирамидам или хайпам. Главный их аргумент заключается в том, что в матрице отсутствует централизация денежных средств.
Действительно, деньги, вносимые участниками, как правило, не стекаются в единые руки, в некий единый фонд, распоряжаться которым может организатор проекта, или небольшая группа участников. Обычно, деньги вообще в самой системе не хранятся, но при оплате уровней производится непосредственный перевод денежных средств с электронного кошелька одного участника на электронный кошелек другого участника.
Вообще, матричные проекты нередко позиционируют себя как благотворительные общества и кассы взаимопомощи, где каждый участник оказывает денежную помощь своему спонсору и получает помощь от своих рефералов.
Матричные проекты можно ли заработать
Все матричные проекты обещают своим участникам лавинообразный денежный поток на их электронные кошельки (обычно в платежных системах QIWI, Perfect Money, Payeer или Bitcoin). Действительно, теоретически, количество денег, поступающих на электронный кошелек участника матрицы, должно увеличиваться в геометрической прогрессии, по мере роста создаваемой им структуры.
Однако на практике все не так просто, и гарантий того, что участник, хотя бы, вернет назад потраченные средства, нет никаких. Впрочем, нередко стартовая сумма для участия в проекте более чем символична — в некоторых проектах она составляет от 1 до 10 рублей.
Хотя существуют отдельные проекты, которые прибегают к различным махинациям со скриптами, в результате которых участник посылает деньги не своему спонсору, а админу, нельзя рассматривать матричные проекты в целом, как однозначное мошенничество.
Ведь тот, кто смог пригласить рефералов, деньги свои получает. И организаторы проекта никак не замалчивают того, что получение дохода возможно только при построении структуры. И именно построение структуры и является основным камнем преткновения.
Действительно, теоретически, матрицы потенциально являются наиболее эффективным способом заработка практически с нуля. Мало того, других способов за короткий срок получить прибыль, в десятки и сотни раз превышающую вложения, пожалуй, не существует даже потенциально. Однако, что, в действительности, происходит на практике?
[tip] Зарабатывает в любом случае, безусловно, сам админ, поскольку, если он создал проект с выгодными условиями и организовал рекламную компанию, желающие присоединиться к этому проекту найдутся. [/tip]
Выводы
Не остаются в проигрыше и профессиональные рефоводы — те, кто годами занимаются привлечением рефералов и имеют отлаженную схему приглашений (например, ведут блог с высокой посещаемостью и большим количеством подписчиков, или имеют раскрученный канал на Ютюбе).
Те, рефоводы-профессионалы, которые рано узнали о новом проекте, достаточно быстро создадут целевой трафик на свои реферальные ссылки.
Что-то заработают и те, у которых есть круг друзей, интересующихся МЛМ, и готовых принять участие в каком-нибудь новом проекте.
Те же, кто к вышеперечисленным категориям не относятся, могут рассчитывать лишь на то, что им повезет, и они окажутся в нужное время в нужном месте.
Регистрироваться в матричном проекте, или нет — решать вам самим.
И помните, что выбор был ваш. Однако, если вы решили регистрироваться, то действуйте немедля.
В Интернете, как, впрочем, и везде, побеждает самый быстрый. По мере возрастания участников проекта будет возрастать конкуренция — ваших потенциальных клиентов будут уводить у вас из под носа.
Со временем приток новых участников в тот или иной матричный проект ослабевает. Те, кто мог вступить в проект, те уже вступили, а те, кто еще не вступил, те уже и не вступят.
И поскольку жизнь таких проектов целиком зависит от притока новых участников, то с уменьшением числа новых регистраций проект замораживается. Потому, матричные проекты, как правило, недолговечны.
Источник
Математика для чайников. Матрицы и основные действия над ними
1-й курс, высшая математика, изучаем матрицы и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Элементы, для которых i=j (a11, a22, .. ) образуют главную диагональ матрицы, и называются диагональными.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:
И пример с реальными числами. Умножим матрицы:
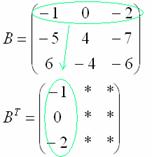
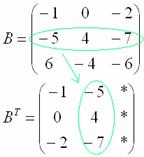
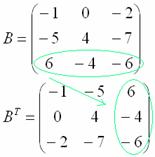
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот — столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис. Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.
Источник
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: 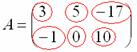
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: 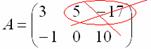
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки: 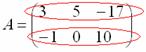
и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 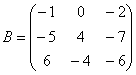
Если в матрице один столбец 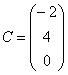
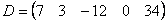
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: 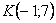
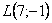
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице 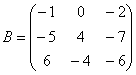
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: 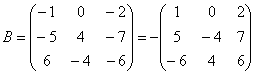
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: 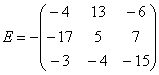
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
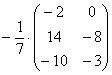
Сначала рассмотрим то, чего делать НЕ НАДО: 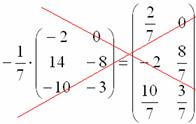
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 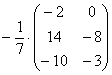
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В этом случае можно и НУЖНО умножить все элементы матрицы на 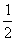
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Транспонировать матрицу
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
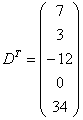
Транспонированная матрица обычно обозначается надстрочным индексом 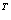
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
Потом переписываем вторую строку во второй столбец:
И, наконец, переписываем третью строку в третий столбец:
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Сложить матрицы 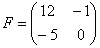
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Найти разность матриц 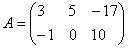
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу 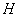
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу 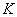
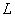
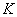
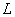
Пример:
Можно ли умножить матрицу 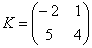
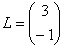
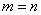
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
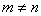
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 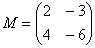
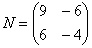
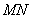
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Умножить матрицу 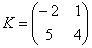
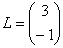
Я буду сразу приводить формулу для каждого случая:
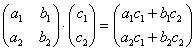
Умножить матрицу 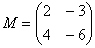
Формула:
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение 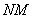
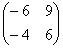
Обратите внимание, что 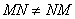
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу 
Переходим к матрицам третьего порядка:
Умножить матрицу 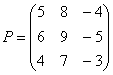
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 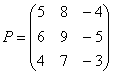
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник