Что значит проверить матрицу

Сайт Виктора Королева

Простыми словами о ремонте телевизоров и домашней бытовой техники своими руками

Матрица – принцип работы, проверка и восстановление

Матрица – принцип работы, проверка и восстановление

Основной элемент LCD-панели или попросту монитора – жидкокристаллическая матрица, представляющая собой законченный функциональный модуль с набором входных сигналов, определяемых его архитектурой. Поэтому все образцы этих устройств построены примерно одинаково, а их проверка и ремонт проводятся в виде стандартных процедур.

Устройство и порядок работы

Матрица представляет собой комбинацию большого числа жидких кристаллических ячеек, располагающихся системно. Характерным для нее является то, что положение каждого из этих элементов описывается двумя координатами: номерами строк и столбцов.

С другой стороны, в ее конструкции предусмотрены следующие модули (смотрите фото ниже):

• Рабочий интерфейс LVDS.
• Микроконтроллер TCON.
• Плата управления (ПУ) питающими напряжениями.
• Модуль задней подсветки (инвертор).

Обратите внимание: Последний компонент имеется не у всех моделей LCD-панелей.

Первый из модулей (интерфейс LVDS) обеспечивает высокую скорость приема данных и существенное снижение линейных помех. Благодаря этому узлу панель приобретает универсальные свойства, позволяющие эксплуатировать ее с любой управляющей платой, имеющей аналогичный интерфейс.

При его использовании информация на ЖК-панель передается в последовательном виде – поэтому в ее составе предусмотрен специальный чип, преобразующий данные в параллельный код. Он представляет собой интегральную микросхему, выполняющую функцию приемника. Далее данные в параллельном коде поступают на микросхему контроллера TCON.

Вторая составляющая матрицы обеспечивает выполнение следующих операций:

1. Управление синхронизацией и приемом данных.
2. Распределение ее по драйверам строк и столбцов.
3. Выдача управляющих сигналов на выход.

На выходном шлейфе контроллера формируется столько сигналов, сколько необходимо для управления транзисторами, встроенными в панель. Общее их количество определяется разрешением, которое поддерживается данным конкретным образцом матрицы. При разрешении 1600х1200, например, на экране будет 1200 строк и 4800 столбцов (1600х3).

Дополнительная информация: Умножение на 3 означает, что каждый цветной элемент формируется на базе трех располагающихся рядом точек.

В панелях большинства марок используется полосковая топология, называемая Stripe. Пример расположения точек на поверхности матрицы приводится на фото снизу.

Характерные неисправности

К числу основных проблем, чаще всего возникающих при эксплуатации матриц, следует отнести:

• Монитор не включается, а светодиод индикатора питания не светится.
• Слишком низкая или очень высокая яркость картинки.
• Изображение на экране мигает (все или только один край).
• Темный экран (индикатор питания горит).
• Экранная подсветка гаснет через какое-то время.
• Отсутствует один цвет.

Рассмотрим каждую из неисправностей более подробно.

В первом случае, возможно, вышел из строя внутренний источник питания, который можно попробовать отремонтировать. Однако специалисты советуют при наличии возможностей сразу заменить его новым изделием (сделать это можно, если он оформлен как отдельный модуль). В ситуации, когда источник входит в состав управляющей платы – придется полностью обновить этот узел. Причиной этой неполадки также могут быть:

• Выход из строя сетевого адаптера (в моделях, где он имеется).
• Неисправность кнопки включения.
• Неполадки в самой ПУ.

Для устранения этих нарушений сначала нужно проверить «подозрительную» деталь, модуль или плату с помощью тестера (на предмет наличия нужных напряжений и отсутствия обрывов в рабочих цепях). При обнаружении поврежденных узлов или элементов плату, адаптер или кнопку придется заменить.

При выявлении неисправности второго рода (изменился уровень яркости) причину следует искать в нарушениях в работе инвертора, лампочек задней подсветки или ПУ. После проверки импульсных напряжений на выходе инвертора и управляющей платы можно будет убедиться в их состоянии.

Важно! Для получения полной картины с управляющими сигналами удобнее всего воспользоваться цифровым осциллографом.

Если нужные импульсные напряжения на выходе этих узлов отсутствуют – потребуется заменить их исправными. При наличии всех сигналов можно попробовать обновить лампочки подсветки. В ряде моделей следует начинать с проверки соединительного шлейфа между инвертором и ПУ на предмет его целостности.

При мигающем экране неисправными могут быть инвертор или лампа задней подсветки. Для устранения этой неисправности придется проделать все те же операции, что и в предыдущем случае. При обнаружении нарушений в формировании импульсных сигналов или обрыва шлейфа – необходимо заметь эти элементы новыми изделиями. Неисправную лампочку подсветки также потребуется обновить.

При наличии опыта соответствующих работ можно попытаться отремонтировать инвертор своими руками. Однако в этом случае надеяться на положительный результат можно не всегда. Если экран потемнел и ни изменяет свое состояние (фото ниже) – нужно проверить преобразователь в плате ПУ или инвертор.

В первом случае следует убедиться с помощью тестера в наличии напряжений у всех стабилизаторов и при обнаружении нарушений заменить неисправный элемент новой деталью. При выявлении отклонений в работе инвертора проще всего заменить его рабочим аналогом.

Если экран выключается через неопределенное время – нарушение, скорее всего, кроется в срабатывании токовой защиты инвертора. Другой причиной может быть неисправность лампочки задней подсветки. Для решения вопроса в этом случае рекомендуется заменить оба узла.

В ситуации, когда отсутствует один из цветов в изображении – неисправность может скрываться в нарушении работы интерфейса или ПУ. Если их проверка подтвердила эти предположения – вышедшие из строя узлы следует заменить. В заключение отметим, что к самостоятельному ремонту матрицы монитора не следует приступать, если вы полностью не уверены в своих силах.

Источник

Проверяем матрицу ноутбука на работоспособность

Проверка матрицы с помощью специальной утилиты

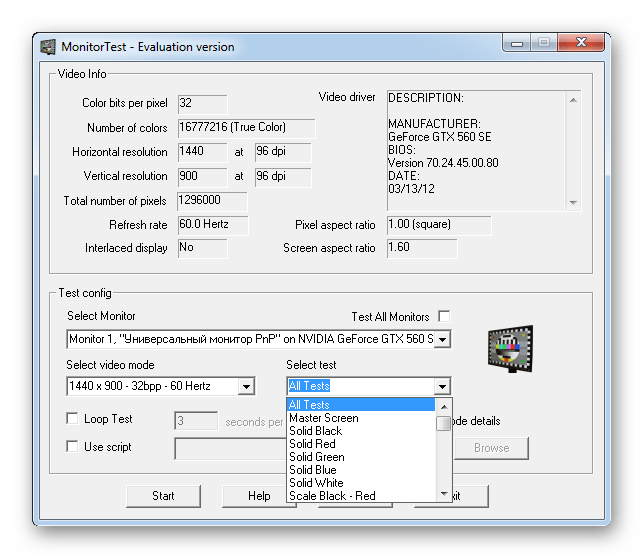
Самый эффективный способ проверить работоспособность матрицы на ноутбуке – это использовать стороннее программное обеспечение, например PassMark MonitorTest. Подробная инструкция о том, как правильно настроить программу, а также протестировать параметры экрана, есть в нашей обзорной статье.

Возможные проблемы

Если матрица ноутбука передает искаженное изображение, отображает неправильные цветовые оттенки, то проблема может быть как программная, так и аппаратная.

Искажение цветов / однотонный цвет

Наиболее распространенные неисправности, связанные с цветными искажениями и отсутствием прежней яркости, описаны в других наших статьях по ссылкам ниже.

Подробнее:
Тусклый экран на ноутбуке: что делать
Зеленый экран монитора: что делать
Белый экран при включении ноутбука

Битые пиксели

Для экспресс-проверки монитора ноутбука пользователи выбирают поиск на нем битых пикселей. Это актуально при покупке нового устройства или б/у. Провести такого рода проверку можно как при помощи онлайн-сервисов, так и устанавливаемых в систему программ. Вся сопутствующая информация есть по ссылкам ниже.

Артефакты

В некоторых случаях, если вы видите непонятные полосы, точки (все, что называется артефактами на экране), виновата может оказаться не матрица, а видеокарта. Используя ссылку ниже, проверьте и ее, чтобы точно понять, в каком именно компоненте кроется неполадка.

Аппаратная поломка

Если матрица неисправна и требует замены, то благодаря другому нашему материалу можно узнать, как правильно это сделать. Конечно, инструкция подойдет только для людей, разбирающихся в подобных манипуляциях, всем остальным понадобится обратиться в сервисный центр за квалифицированной помощью.

Подробнее: Замена матрицы на ноутбуке

Помимо этой статьи, на сайте еще 12534 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Источник

Нахождение обратной матрицы: три алгоритма и примеры

Что значит найти обратную матрицу?

Нахождение обратной матрицы — процесс, который состоит из достаточно простых действий. Но эти действия повторяются так часто, что процесс получается довольно продолжительным. Главное — не потерять внимание при решении.

При решении наиболее распространённым методом — алгебраических дополнений — потребуется:

• вычислять определители, поэтому нелишне открыть в новом окне материал по вычислению определитедей;
• находить миноры и алгебраические дополнения — подробно об этом также в соответствующем материале;
• транспонировать матрицы.

При решении примеров мы разберём эти действия подробнее. А пока узнаем, что гласит теория об обратной матрице.

Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1 . Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.

Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица

,

произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)

Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.

Нахождение обратной матрицы — задача, которая чаще решается двумя методами:

• методом алгебраических дополнений, при котором, как было замечено в начале урока, требуется находить определители, миноры и алгебраические дополнения и транспонировать матрицы;
• методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).

Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.

Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.

Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.

Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.

На сайте есть онлайн калькулятор для нахождения обратной матрицы. Вы можете открыть его в новом окне уже сейчас, если держите перед собой ваши собственные задания. А мы разберём несколько разминочных.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

, (2)

где — определитель матрицы А, а — матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается, если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Вычислим алгебраическое дополнение элемента , то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента получим, если умножим , где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента :

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы , транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу , транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:

Следовательно, матрица , союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Нахождение обратной матрицы методом исключения неизвестных Гаусса

Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса — приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы получим сдвоенную матрицу . Умножим обе части этой матрицы на , тогда получим

,

и .

Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса

1. К матрице A приписать единичную матрицу того же порядка.

2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.

2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.

Пример 2. Для матрицы

найти обратную матрицу.

Решение. Составляем сдвоенную матрицу

и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.

Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим

.

Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим

.

Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим

.

Разделим третью строку на 8, тогда

.

Умножим третью строку на 2 и сложим её со второй строкой. Получается:

.

Переставим местами вторую и третью строку, тогда окончательно получим:

.

Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:

.

Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:

.

В результате должна получиться обратная матрица.

Пример 3. Для матрицы

найти обратную матрицу.

Решение. Составляем сдвоенную матрицу

и будем её преобразовывать.

Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим

.

Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим

.

Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.

Нахождение обратной матрицы методом линейных преобразований

Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.

Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование — это система линейных уравнений, вид которой будет приведён ниже в алгоритме.

Алгоритм нахождения обратной матрицы методом линейных преобразований

1. Для данной невырожденной матрицы A составить линейное преобразование — систему линейных уравнений вида

,

где a ij — элементы матрицы A.

2. Решить полученную систему относительно y — найти для предыдущего линейного преобразование обратное линейное преобразование

,

в котором A ij — алгебраические дополнения элементов матрицы A, Δ — определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки — в столбце, а для элементов столбца — в строке.

3. Находим коэффициенты при y: , которые и будут элементами матрицы, обратной для матрицы A.

4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.

Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований — это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.

Пример 4. Найти обратную матрицу для матрицы

.

Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.

Для данной матрицы записываем линейное преобразование:

.

Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:

Коэффициенты при иксах в обратном линейном преобразовании — это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:

Найти обратную матрицу самостоятельно, а затем посмотреть решение

Пример 5. Найти обратную матрицу для матрицы

.

Источник