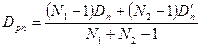Что значит проверить адекватность модели объекту оригиналу

Проверка адекватности модели

При моделировании исследователя прежде всего интересует, насколько хорошо модель представляет моделируемую систему (объект моделирования). Модель, поведение которой слишком отличается от поведения моделируемой системы, практически бесполезна.

Различают модели существующих и проектируемых систем.

Если реальная система (или ее прототип) существует, дело обстоит достаточно просто. Поэтому для моделей существующих систем исследователь должен выполнить проверку адекватности имитационной модели объекту моделирования, т.е. проверить соответствие между поведением реальной системы и поведением модели.

На реальную систему воздействуют переменные G*, которые можно измерять, но нельзя управлять, параметры Х*, которые исследователь может изменять в ходе натурных экспериментов. На выходе системы возможно измерение выходных характеристикY*.

При этом существует некоторая неизвестная исследователю зависимость между ними Y*=f*(Х*, G*).

Имитационную модель можно рассматривать как преобразователь входных переменных в выходные. В любой имитационной модели различают составляющие: компоненты, переменные, параметры, функциональные зависимости, ограничения, целевые функции. Модель системы определяется как совокупность компонент, объединенных для выполнения заданной функции Y = f(Х, G).Здесь Y, Х, G — векторы соответственно результата действия модели системы выходных переменных, параметров моделирования, входных переменных модели. Параметры модели Х исследователь выбирает произвольно, G -принимают только те значения, которые характерны для данных объекта моделирования.

Очевидный подход в оценке адекватности состоит в сравнении выходов модели и реальной системы при одинаковых (если возможно) значениях входов. И те, и другие данные (данные, полученные на выходе имитационной модели и данные, полученные в результате эксперимента с реальной системой) — статистические. Поэтому применяют методы статистической теории оценивания и проверки гипотез.

Используя соответствующий статистический критерий для двух выборок, мы можем проверить статистические гипотезы (Н₀) о том, что выборки выходов системы и модели являются выборками из различных совокупностей или (Н₁), что они «практически» принадлежат одной совокупности.

Могут быть рекомендованы два основных подхода к оценке адекватности:

1 способ: по средним значениям откликов модели и системы.

Проверяется гипотеза о близости средних значений каждый n-й компоненты откликов модели Y_n известным средним значениям n-й компоненты откликов реальной системы .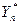

Проводят N₁ опытов на реальной системе и N₂опытов на имитационной модели (обычно N₂ > N₁).

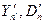
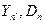
Оценивают для реальной системы и имитационной модели математическое ожидание и дисперсию, и соответственно.

Гипотезы о средних значениях проверяются с помощью критерия f-Стьюдента, можно использовать параметрический критерий Манны-Уитни и др.

Например, продемонстрируем использование f-статистики. Основой проверки гипотез является E_n = (Y_n -Y’_n), оценка её дисперсии:

.

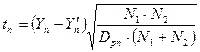
Берут таблицу распределения t-статистики с числом степеней свободы:
g = N₁ + N₂ — 2 (обычно с уровнем значимости a = 0,05). По таблицам находят критическое значение t_кр. Если t_n £ t_кр, гипотеза о близости средних значений n-й компоненты откликов модели и системы принимается. И т.д. по всем n компонентам вектора откликов.

2 способ: по дисперсиям отклонений откликов модели от среднего значения откликов систем.

Сравнение дисперсии проводят с помощью критерия F (проверяют гипотезы о согласованности), с помощью критерия согласия ? 2 (при больших выборках, п>100), критерия Колмогорова- Смирнова (при малых выборках, известны средняя и дисперсия совокупности), Кохрена и др.

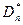
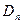
Проверяется гипотеза о значимости различий оценок двух дисперсий: и .

Составляется F-статистика: 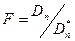(задаются обычно уровнем значимости
a = 0,05, при степенях свободы 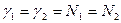), по таблицам Фишера для F-распределения находят F_кр. Если F > F_кр, гипотеза о значимости различий двух оценок дисперсий принимается, значит — отсутствует адекватность реальной системы и имитационной модели по n-ой компоненте вектора отклика.

Процедура повторяется аналогичным образом по всем компонентам вектора отклика. Если хотя бы по одной компоненте адекватность отсутствует, то модель неадекватна. В последнем случае, если обнаружены незначительные отклонения в модели, может проводиться калибровка имитационной модели (вводятся поправочные, калибровочные коэффициенты в моделирующий алгоритм), с целью обеспечения адекватности.

А если не существует реальной системы (что характерно для задач проектирования, прогнозирования)? Проверку адекватности выполнить в этом случае не удается, поскольку нет реального объекта. Для целей исследования модели иногда проводят специальные испытания (например, так поступают при военных исследованиях). Это позволяет убедиться в точности модели, полезности ее на практике, несмотря на сложность и дороговизну проводимых испытаний.

Могут использоваться и другие подходы к проведению валидации имитационной модели [56], кроме статистических сравнений между откликами реальной системы и модели. В отдельных случаях полезна валидация внешнего представления, когда проверяется насколько модель выглядит адекватной с точки зрения специалистов, которые с ней будут работать, так называемый тест Тьюринга (установление экспертами различий между поведением модели и реальной системы). В процессе валидации требуется постоянный контакт с заказчиком модели, дискуссии с экспертами по системе. Рекомендуется также проводить эмпирическое тестирование допущений модели, в ходе которого может осуществляться графическое представление данных, проверка гипотез о распределениях, анализ чувствительности и др. Важным инструментом валидации имитационной модели является графическое представление промежуточных результатов и выходных данных, а также анимация процесса моделирования. Наиболее эффективными являются такие представления данных, как гистограммы, временные графики отдельных переменных за весь период моделирования, графики взаимозависимости, круговые и линейчатые диаграммы. Методика применения статистических технологий зависит от доступности данных по реальной системе.

Источник

Процесс Data Mining. Построение и использование модели

Этап 5. Проверка и оценка моделей

Проверка модели подразумевает проверку ее достоверности или адекватности . Эта проверка заключается в определении степени соответствия модели реальности. Адекватность модели проверяется путем тестирования.

Адекватность модели (adequacy of a model ) — соответствие модели моделируемому объекту или процессу.

Понятия достоверности и адекватности являются условными, поскольку мы не можем рассчитывать на полное соответствие модели реальному объекту, иначе это был бы сам объект , а не модель . Поэтому в процессе моделирования следует учитывать адекватность не модели вообще, а именно тех ее свойств, которые являются существенными с точки зрения проводимого исследования. В процессе проверки модели необходимо установить включение в модель всех существенных факторов. Сложность решения этой проблемы зависит от сложности решаемой задачи.

Проверка модели также подразумевает определение той степени, в которой она действительно помогает менеджеру при принятии решений.

Оценка модели подразумевает проверку ее правильности. Оценка построенной модели осуществляется путем ее тестирования.

Тестирование модели заключается в «прогонке» построенной модели , заполненной данными, с целью определения ее характеристик, а также в- проверке ее работоспособности. Тестирование модели включает в себя проведение множества экспериментов. На вход модели могут подаваться выборки различного объема. С точки зрения статистики, точность модели увеличивается с увеличением количества исследуемых данных. Алгоритмы, являющиеся основой для построения моделей на сверхбольших базах данных, должны обладать свойством масштабирования.

Если модель достаточно сложна, а значит, требуется много времени на ее обучение и последующую оценку , то иногда бывает можно построить и протестировать модель на небольшой части выборки. Однако этот вариант подходит только для однородных данных, в противном случае необходимо использовать все доступные данные [98]. Построенные модели рекомендуется тестировать на различных выборках для определения их обобщающих способностей. В ходе экспериментов можно варьировать объем выборки (количество записей), набор входных и выходных переменных, использовать выборки различной сложности.

Выявленные соотношения и закономерности должны быть проанализированы экспертом в предметной области — он поможет определить, как являются выясненные закономерности (возможно, слишком общими или узкими и специфическими).

Для оценки результатов полученных моделей следует использовать знания специалистов предметной области . Если результаты полученной модели эксперт считает неудовлетворительными, следует вернуться на один из предыдущих шагов процесса Data Mining , а именно: подготовка данных, построение модели , выбор модели .

Если же результаты моделирования эксперт считает приемлемыми, ее можно применять для решения реальных задач.

Этап 6. Выбор модели

Если в результате моделирования нами было построено несколько различных моделей , то на основании их оценки мы можем осуществить выбор лучшей из них. В ходе проверки и оценки различных моделей на основании их характеристик, а также с учетом мнения экспертов, следует выбор наилучшей. Достаточно часто это оказывается непростой задачей.

Основные характеристики модели , которые определяют ее выбор, — это точность модели и эффективность работы алгоритма [77].

В некоторых программных продуктах реализован ряд методов, разработанных для выбора модели . Многие из них основаны на так называемой «конкурентной оценке моделей «, которая состоит в применении различных моделей к одному и тому же набору данных и последующем сравнении их характеристик.

Например, в пакете Statistica (Statsoft) [39] эти методы рассматриваются как ядро «предсказывающей добычи данных», они включают: накопление (голосование, усреднение); бустинг; мета-обучение.

Этап 7. Применение модели

После тестирования, оценки и выбора модели следует этап применения модели . На этом этапе выбранная модель используется применительно к новым данным с целью решения задач, поставленных в начале процесса Data Mining . Для классификационных и прогнозирующих моделей на этом этапе прогнозируется целевой (выходной) атрибут ( target attribute ).

Этап 8. Коррекция и обновление модели

По прошествии определенного установленного промежутка времени с момента начала использования модели Data Mining следует проанализировать полученные результаты, определить, действительно ли она «успешна» или же возникли проблемы и сложности в ее использовании.

Однако даже если модель с успехом используется, ее не следует считать абсолютно верной на все времена. Дело в том, что необходимо периодически оценивать адекватность модели набору данных, а также текущей ситуации (следует учитывать возможность изменения внешних факторов). Даже самая точная модель со временем перестает быть таковой. Для того чтобы построенная модель выполняла свою функцию, следует работать над ее коррекцией (улучшением). При появлении новых данных требуется повторное обучение модели . Этот процесс называют обновлением модели . Работы, проводимые с моделью на этом этапе, также называют контролем и сопровождением модели .

Существует много причин, требующих обучить модель заново, т.е. обновить ее, чтобы отразить определенные изменения.

Основными причинами являются следующие:

• изменились входящие данные или их поведение;
• появились дополнительные данные для обучения;
• изменились требования к форме и количеству выходных данных;
• изменились цели бизнеса, которые повлияли на критерии принятия решений;
• изменилось внешнее окружение или среда (макроэкономика, политическая ситуация, научно-технический прогресс, появление новых конкурентов и товаров и т.д.).

Причины, перечисленные выше, могут обесценить допущения и исходную информацию, на которых основывалась модель при построении.

Приведем простой пример из задачи о туристическом агентстве.

Рассматриваемое правило гласит: «Если ДОХОД>20 и СЕМЕЙНОЕ ПОЛОЖЕНИЕ = «married», то класс «1». Эта модель может успешно работать на протяжении какого-то периода, но затем, например, в силу инфляции в стране, модель должна быть скорректирована. В результате рассматриваемое правило может выглядеть таким образом: «Если ДОХОД>30 и СЕМЕЙНОЕ ПОЛОЖЕНИЕ = «married», то класс «1».

Источник