Пространство элементарных событий
В этой лекции мы изложим теоретико-множественный подход к основным понятиям теории вероятностей. Пусть проводится некоторый эксперимент со случайным исходом. Результатом эксперимента всегда является один и только один исход из полной группы несовместных событий. Каждый такой исход называют элементарным событием (или элементарным исходом) и обозначают буквой w. Совокупность всех элементарных событий, которые могут появится в эксперименте, называют пространством элементарных событий и обозначают буквой W.
В теоретико-множественной трактовке любое событие А представляет собой некоторое подмножество А=<w> пространства элементарных событий W. Событие А происходит или нет в зависимости от того, принадлежит или нет подмножеству А элементарное событие w, представляющее исход данного опыта. Таким образом, событие А есть подмножество множества W, состоящее из элементарных исходов w, которые благоприятствуют событию А. Поэтому, в дальнейшем, не будем делать различий между событием А и соответствующим подмножеством АÌW.
Среди событий, являющихся подмножеством множества W, можно рассмотреть и само множество W; оно называется достоверным событием. Ко всему пространству W еще добавляется пустое множество Æ; это множество тоже рассматривается как событие и называется невозможным событием.
Для математической формализации модели случайного эксперимента требуется в первую очередь построить пространство элементарных событий W. Однако поскольку понятие «элементарный исход» строго не определено, то задача построения пространства элементарных событий допускает несколько решений. На практике построение такого множества осуществляется из требования, чтобы все интересующие нас результаты данного эксперимента однозначно описывались на основе построенного множества.
Пример 2.1. Пусть эксперимент состоит в подбрасывании один раз игральной кости. Обозначим через X число выпавших очков. Построить пространство элементарных событий W и указать состав подмножеств, соответствующих следующим событиям: A=
Решение. Очевидно, что за элементарные события здесь лучше всего взять события: <1>, <2>, <3>, <4>, <5>, <6>, которые образуют полную группу несовместных событий. При помощи этих элементарных событий можно легко описать все перечисленные в задаче события:
Отметим, что при решении вероятностных задач построение пространства элементарных событий играет большую роль. Если это пространство построено удачно, то решение задач может значительно упроститься; в противном случае она может представлять значительные трудности или даже вообще не будет найдено. Так, в рассматриваемой задаче за элементарные события можно было бы взять события: w1=
Алгебра событий
Поскольку при теоретико-множественном подходе к теории вероятностей события отождествляются с множествами, то над событиями можно совершать те же самые операции, что и для множеств. В частности:
| Алгебра событий | Алгебра множеств | ||
| AÌB | событие А влечет за собой событие В | AÌB | множество А является подмножеством множества В |
| A=B | событие А тождественно событию В | A=B | равенство множеств |
| A+B | сумма событий, означающее, что произошло хотя бы одно из двух событий | AÈB | объединение множеств |
| A×B | произведение событий, означающее, что оба события произойдут одновременно | AÇB | пересечение множеств |
| A–B | разность событий, означающее, что произойдет событие А, но не произойдет событие В | A \ B | разность множеств, т.е. множество элементов, принадлежащих А, но не принадлежащих В |
| =W–A | противоположное событие, означающее, что событие А не произойдет | =W \ A | дополнение множества А до W |
Если события А и В несовместны, то А×В=Æ; если события А1, А2, . Аk образуют полную группу, то А1+А2+. +Аk =W. В частности, противоположные события A и 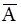
Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Вьенна:
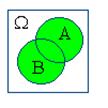 | 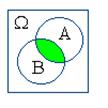 | 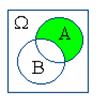 | 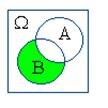 | 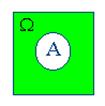 |
| A+B | AB | A–B | B–A | |
Пример 2.2. Эксперимент состоит в подбрасывании двух игральных костей. Обозначим через X сумму очков, выпадавших на обоих костях. Пространство элементарных событий такого эксперимента можно записать в виде W=<2;3;4;5;6;7;8;9;10;11;12>. Описать следующие события A+B, AB, A–B, B–A, если A=
| A+B=<3;5;6;7;9;11;12>, | A–B=<6;12>, |
| AB=<3;9>, | B–A=<5;7;11>. |
Пример 2.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, B, A+B, A–B, если A=<вынутая карта – туз>, B=<вынутая карта – черви>.
Ответ:
Пример 2.3. Пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, описать следующие события: а) произошло только событие А; б) произошло одно событие; в) произошло хотя бы одно событие.
Ответ:
а) 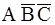
б) 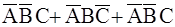
в) A+B+C = 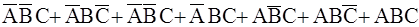
Операции сложения (объединения) и умножения (пересечения) события обладают рядом свойств, аналогичных свойствам обычных операций над числами:
| 1а. A+B = B+A, | 1б. AB = BA, |
| 2а. A+(B+C) = (A+B)+C, | 2б. A(BC) = (AB)C. |
Это свойства коммутативности и ассоциативности. При этом, пустое множество Æ и само базисное множество W аналогичны нулю и единице, соответственно:
| 3а. A+Æ = A, | 3б. AW = A. |
Однако некоторые свойства не имеют аналогов в обычных операциях над числами; в частности:
| 4а. A+A = A, | 4б. AA = A. |
Это свойства идемпотентности. При введении операций всегда возникает вопрос, какая из двух операций больше «похожа» на сложение, а какая на умножение. Ответ на этот вопрос дают свойства дистрибутивности. Однако для алгебры событий (соответственно, и для алгебры множеств) удивительным образом выполняются оба свойства дистрибутивности:
В теоретико-множественной трактовке эти свойства выглядят более симметрично:
| 5а. (AÈB)ÇC = (AÇC)È(BÇC), | 5б. (AÇB)ÈC = (AÈC)Ç(BÈC). |
Эти равенства характеризуют принцип двойственности алгебры событий и показывают равноправие обоих операций. Так, если будет доказана истинность какого-либо тождества, то истинным будет и двойственное ему тождество, т.е. то, которое получается из данного взаимной заменой символов «+» и «×» (или «È» и «Ç»), а также Æ и W. Поэтому все приводимые равенства сгруппированы в пары. Запишем еще несколько свойств:
| 6а. (AB)+A = A, | 6б. (A+B)A = A, | |
| 7а. A+ = W, | 7б. A = Æ, | |
| 8. ` = A, | ||
| 9а. `Æ = W, | 9а. `W = Æ, | |
| 10а. A+W = W, | 10б. AÆ = Æ, | |
11а. 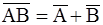 , , | 11б. 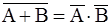 . . | Законы де Моргана |
Система подмножеств множества W, обладающая приведенными свойствами, называется булевой алгеброй. К булевым алгебрам относятся алгебра множеств, алгебра событий и алгебра логики.
Пример 3.4. Покажите, что события A, 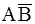
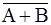
Решение. Покажем, что сумма данных событий образует достоверное событие. Используя законы де Моргана и другие свойства событий, получим:
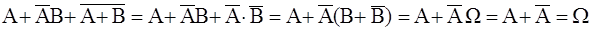
Следовательно, данные события образуют полную группу. Чтобы доказать несовместность данных событий, найдем их попарные произведения:
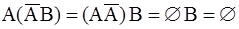
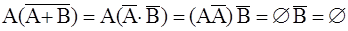
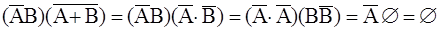
Таким образом, данные в задаче события попарно несовместны. Следовательно, эти события образуют полную группу несовместных события, т.е. образуют пространство элементарных событий.
Источник
Что значит пространство элементарных событий
оЕ ЧУЕ УМХЮБКОЩЕ СЧМЕОЙС (ЬЛУРЕТЙНЕОФЩ) НПЦОП ЙЪХЮБФШ НЕФПДБНЙ ФЕПТЙЙ ЧЕТПСФОПУФЕК, Б МЙЫШ ФЕ, ЛПФПТЩЕ НПЗХФ ВЩФШ ЧПУРТПЙЪЧЕДЕОЩ Ч ПДОЙИ Й ФЕИ ЦЕ ХУМПЧЙСИ. уМХЮБКОПУФШ Й ИБПУ ОЕ ПДОП Й ФП ЦЕ. пЛБЪЩЧБЕФУС, ЮФП Й Ч УМХЮБКОЩИ ЬЛУРЕТЙНЕОФБИ ОБВМАДБАФУС ОЕЛПФПТЩЕ ЪБЛПОПНЕТОПУФЙ, ОБРТЙНЕТ УЧПКУФЧП «УФБФЙУФЙЮЕУЛПК ХУФПКЮЙЧПУФЙ» : ЕУМЙ ОЕЛПФПТПЕ УПВЩФЙЕ, НПЗХЭЕЕ РТПЙЪПКФЙ ЙМЙ ОЕ РТПЙЪПКФЙ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, ФП ДПМС ЬЛУРЕТЙНЕОФПЧ, Ч ЛПФПТЩИ ДБООПЕ УПВЩФЙЕ РТПЙЪПЫМП, ЙНЕЕФ ФЕОДЕОГЙА УФБВЙМЙЪЙТПЧБФШУС У ТПУФПН ПВЭЕЗП ЮЙУМБ ЬЛУРЕТЙНЕОФПЧ , РТЙВМЙЦБСУШ Л ОЕЛПФПТПНХ ЮЙУМХ . ьФП ЮЙУМП УМХЦЙФ ПВЯЕЛФЙЧОПК ИБТБЛФЕТЙУФЙЛПК «УФЕРЕОЙ ЧПЪНПЦОПУФЙ» УПВЩФЙА РТПЙЪПКФЙ.
уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.
рТЙНЕТЩ УПВЩФЙК: ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
рТЙНЕТЩ УПВЩФЙК:
РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
1. дПУФПЧЕТОЩН ОБЪЩЧБЕФУС УПВЩФЙЕ, ЛПФПТПЕ ПВСЪБФЕМШОП РТПЙУИПДЙФ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, Ф.Е. ЕДЙОУФЧЕООПЕ УПВЩФЙЕ, ЧЛМАЮБАЭЕЕ ЧУЕ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ УПВЩФЙЕ .
2. оЕЧПЪНПЦОЩН ОБЪЩЧБЕФУС УПВЩФЙЕ, ЛПФПТПЕ ОЕ НПЦЕФ РТПЙЪПКФЙ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, Ф.Е. УПВЩФЙЕ, ОЕ УПДЕТЦБЭЕЕ ОЙ ПДОПЗП ЬМЕНЕОФБТОПЗП ЙУИПДБ («РХУФПЕ НОПЦЕУФЧП» ). ъБНЕФЙН, ЮФП ЧУЕЗДБ .
1. пВЯЕДЙОЕОЙЕН УПВЩФЙК Й ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМП МЙВП , МЙВП , МЙВП ПВБ УПВЩФЙС ПДОПЧТЕНЕООП. оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЕУФШ НОПЦЕУФЧП, УПДЕТЦБЭЕЕ ЛБЛ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ ЙЪ НОПЦЕУФЧБ , ФБЛ Й ЬМЕНЕОФБТОЩЕ ЙУИПДЩ ЙЪ НОПЦЕУФЧБ .
2. рЕТЕУЕЮЕОЙЕН УПВЩФЙК Й ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМЙ ПВБ УПВЩФЙС Й ПДОПЧТЕНЕООП. оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЕУФШ НОПЦЕУФЧП, УПДЕТЦБЭЕЕ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ, ЧИПДСЭЙЕ Ч РЕТЕУЕЮЕОЙЕ НОПЦЕУФЧ Й .
3. рТПФЙЧПРПМПЦОЩН (ЙМЙ ДПРПМОЙФЕМШОЩН) Л УПВЩФЙА ОБЪЩЧБЕФУС УПВЩФЙЕ , УПУФПСЭЕЕ Ч ФПН, ЮФП УПВЩФЙЕ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ ОЕ РТПЙЪПЫМП. ф.Е. НОПЦЕУФЧП УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ОЕ ЧИПДСЭЙИ Ч .
4. дПРПМОЕОЙЕН УПВЩФЙС ДП ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМП УПВЩФЙЕ , ОП ОЕ РТПЙЪПЫМП . ф.Е. НОПЦЕУФЧП УПДЕТЦЙФ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ, ЧИПДСЭЙЕ Ч НОПЦЕУФЧП , ОП ОЕ ЧИПДСЭЙЕ Ч .
1. уПВЩФЙС Й ОБЪЩЧБАФ ОЕУПЧНЕУФОЩНЙ , ЕУМЙ .
2. уПВЩФЙС ОБЪЩЧБАФ РПРБТОП ОЕУПЧНЕУФОЩНЙ , ЕУМЙ ДМС МАВЩИ , ЗДЕ , УПВЩФЙС Й ОЕУПЧНЕУФОЩ.
3. зПЧПТСФ, ЮФП УПВЩФЙЕ ЧМЕЮЈФ УПВЩФЙЕ , Й РЙЫХФ , ЕУМЙ ЧУЕЗДБ, ЛБЛ ФПМШЛП РТПЙУИПДЙФ УПВЩФЙЕ , РТПЙУИПДЙФ Й УПВЩФЙЕ . оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЬФП ПЪОБЮБЕФ, ЮФП МАВПК ЬМЕНЕОФБТОЩК ЙУИПД, ЧИПДСЭЙК Ч НОПЦЕУФЧП , ПДОПЧТЕНЕООП ЧИПДЙФ Й Ч НОПЦЕУФЧП , Ф.Е. УПДЕТЦЙФУС Ч .
фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.
нОПЦЕУФЧП УЮЈФОП , ЕУМЙ УХЭЕУФЧХЕФ ЧЪБЙНОП-ПДОПЪОБЮОПЕ УППФЧЕФУФЧЙЕ НЕЦДХ ЬФЙН НОПЦЕУФЧПН Й НОПЦЕУФЧПН ЧУЕИ ОБФХТБМШОЩИ ЮЙУЕМ. уЮЈФОЩНЙ НОПЦЕУФЧБНЙ СЧМСАФУС, ОБРТЙНЕТ, НОПЦЕУФЧП ОБФХТБМШОЩИ ЮЙУЕМ, НОПЦЕУФЧП ГЕМЩИ ЮЙУЕМ, НОПЦЕУФЧП ТБГЙПОБМШОЩИ ЮЙУЕМ, НОПЦЕУФЧП ЮЈФОЩИ ЮЙУЕМ Й Ф.Д. нОПЦЕУФЧП ЛПОЕЮОП , ЕУМЙ ПОП УПУФПЙФ ЙЪ ЛПОЕЮОПЗП ЮЙУМБ ЬМЕНЕОФПЧ.
оБЪПЧЈН ЮЙУМП ЧЕТПСФОПУФША ЬМЕНЕОФБТОПЗП ЙУИПДБ . чЕТПСФОПУФША УПВЩФЙС ОБЪПЧЈН ЮЙУМП
ТБЧОПЕ УХННЕ ЧЕТПСФОПУФЕК ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ЧИПДСЭЙИ Ч НОПЦЕУФЧП . ч УМХЮБЕ РПМПЦЙН .
2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;
3. ч ПВЭЕН УМХЮБЕ ;
еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :
ЗДЕ УЙНЧПМПН ПВПЪОБЮЕОП ЮЙУМП ЬМЕНЕОФПЧ ЛПОЕЮОПЗП НОПЦЕУФЧБ .
ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.
нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.
тБУУНПФТЙН ПРЙУБООЩЕ Ч РБТБЗТБЖЕ 1 ХТОПЧЩЕ УИЕНЩ. фТЙ УИЕНЩ: У ЧПЪЧТБЭЕОЙЕН Й У ХЮЈФПН РПТСДЛБ, ВЕЪ ЧПЪЧТБЭЕОЙС Й У ХЮЈФПН РПТСДЛБ, Б ФБЛЦЕ ВЕЪ ЧПЪЧТБЭЕОЙС Й ВЕЪ ХЮЈФБ РПТСДЛБ, ХДПЧМЕФЧПТСАФ ЛМБУУЙЮЕУЛПНХ ПРТЕДЕМЕОЙА ЧЕТПСФОПУФЙ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ Ч ЬФЙИ УИЕНБИ РПДУЮЙФБОП Ч ФЕПТЕНБИ 4, 2, 3 Й ТБЧОП УППФЧЕФУФЧЕООП , , . юЕФЧЈТФБС ЦЕ УИЕНБ УИЕНБ ЧЩВПТБ У ЧПЪЧТБЭЕОЙЕН Й ВЕЪ ХЮЈФБ РПТСДЛБ ЙНЕЕФ ЪБЧЕДПНП ОЕТБЧОПЧПЪНПЦОЩЕ ЙУИПДЩ.
еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:
рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК ЧЕТПСФОПУФШ 1/4+1/4=1/2.
тЕЫЕОЙЕ. рТЙ ЙМЙ ЙУЛПНБС ЧЕТПСФОПУФШ ТБЧОБ ОХМА, ФБЛ ЛБЛ УППФЧЕФУФЧХАЭЕЕ УПВЩФЙЕ ОЕЧПЪНПЦОП. рХУФШ Й .
тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.
чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП -ЬМЕНЕОФОЩИ РПДНОПЦЕУФЧ НОПЦЕУФЧБ, УПУФПСЭЕЗП ЙЪ ЬМЕНЕОФПЧ: (РП ФЕПТЕНЕ 3).
пВПЪОБЮЙН ЮЕТЕЪ УПВЩФЙЕ, ЧЕТПСФОПУФШ ЛПФПТПЗП ФТЕВХЕФУС ОБКФЙ. уПВЩФЙА ВМБЗПРТЙСФУФЧХЕФ РПСЧМЕОЙЕ МАВПЗП ОБВПТБ, УПДЕТЦБЭЕЗП ВЕМЩИ ЫБТПЧ Й ЮЈТОЩИ. юЙУМП ВМБЗПРТЙСФОЩИ ЙУИПДПЧ ТБЧОП РТПЙЪЧЕДЕОЙА (РП ФЕПТЕНЕ 1) ЮЙУМБ УРПУПВПЧ ЧЩВТБФШ ВЕМЩИ ЫБТПЧ ЙЪ Й ЮЙУМБ УРПУПВПЧ ЧЩВТБФШ ЮЈТОЩИ ЫБТПЧ ЙЪ , Ф.Е. . чЕТПСФОПУФШ УПВЩФЙС ТБЧОБ
чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,
рТЙ РПДУЮЈФЕ ЮЙУМБ ВМБЗПРТЙСФОЩИ ЙУИПДПЧ ОХЦОП ХЮЕУФШ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ ВЕМЩИ Й ЮЈТОЩИ ЫБТПЧ Й ЮЙУМП УРПУПВПЧ ТБУРПМПЦЙФШ ЬФЙ ЫБТЩ УТЕДЙ . нПЦОП, УЛБЦЕН, РПУЮЙФБФШ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ НЕУФ УТЕДЙ (ТБЧОПЕ ), ЪБФЕН ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ОБ ЬФЙИ НЕУФБИ ВЕМЩИ ЫБТПЧ (ТБЧОПЕ ), Й ЪБФЕН ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ОБ ПУФБЧЫЙИУС НЕУФБИ ЮЈТОЩИ ЫБТПЧ (ТБЧОПЕ ). рЕТЕНОПЦЙЧ ( РПЮЕНХ?) ЬФЙ ЮЙУМБ, РПМХЮЙН
(ЗДЕ ФБЛПЧП, ЮФП , Й ) ОБЪЩЧБЕФУС ЗЙРЕТЗЕПНЕФТЙЮЕУЛЙН ТБУРТЕДЕМЕОЙЕН .
ч ЗЙРЕТЗЕПНЕФТЙЮЕУЛПН ТБУРТЕДЕМЕОЙЙ ЕДЙОЙЮОБС ЧЕТПСФОПУФШ ТБУРТЕДЕМЕОБ НЕЦДХ РПДИПДСЭЙНЙ ГЕМЩНЙ ЮЙУМБНЙ ОЕТБЧОПНЕТОП. лБЦДПНХ ГЕМПНХ ЮЙУМХ УПРПУФБЧМЕОБ УЧПС ЧЕТПСФОПУФШ . оБ ЧЕЭЕУФЧЕООПК РТСНПК НПЦОП ЕДЙОЙЮОХА ЧЕТПСФОПУФШ ТБУРТЕДЕМЙФШ РП-ТБЪОПНХ. ьФЙН ПДОП ТБУРТЕДЕМЕОЙЕ ПФМЙЮБЕФУС ПФ ДТХЗПЗП: ФЕН, ОБ ЛБЛПН НОПЦЕУФЧЕ ЮЙУЕМ «ТБУРТЕДЕМЕОБ» ПВЭБС ЕДЙОЙЮОБС ЧЕТПСФОПУФШ, Й ФЕН, ЛБЛЙЕ ЧЕУБ, ЙМЙ ЧЕТПСФОПУФЙ, РТЙУЧПЕОЩ ПФДЕМШОЩН ФПЮЛБН ЙМЙ ЮБУФСН ЬФПЗП НОПЦЕУФЧБ.
1 Jacob Bernoulli (27.12.1654 16.08.1705, Basel, Switzerland) .
Источник


