Что значит промышленные функции

Производственная функция

Существование индивидов в социуме устроено по определенному принципу. Оно состоит в следующем: для своего ежедневного существования люди должны потреблять материальные блага, но перед этим производить их. Процесс производства благ происходит, благодаря действующим закономерностям, позволяющим обеспечивать рынок достаточным ассортиментом продукции.

Для того, чтобы процесс был непрерывным, необходимо взаимодействие всех участвующих факторов производства (капитала, механических и человеческих ресурсов, сырья, уровня технологий и т.д.), которые вместе образуют производственную функцию. Данное понятие представляет собой экономико-математическую зависимость между количеством выпускаемой продукции и факторов производства, которое может выражаться во множестве изоквант.

Свойства функции

Производственная функция имеет собственную формулу и практически отражается на составленных графиках. Она помогает выявить размер получающихся издержек определенного количества товаров, которые пригодятся для их создания. Также функция помогает в интеграции новых разработок, где взаимодействие факторов влияет на показатели полученного результата.

Главные свойства производственной функции – это:

1. Взаимозаменяемость факторов. Пример: труд человека могут выполнять машины или роботы.
2. Факторная взаимодополняемость. Пример: сотрудники нуждаются в инструментах для выполнения рабочих задач.
3. Предельность повышения выпускаемого объема товаров или факторов производства. Пример: необходимо по плану изготовить конкретное количество продукта, или – в цеху одновременно может трудиться некоторое количество специалистов.

Формулу производственной функции часто представляют в следующем виде.

Q = f (K, M, L, T, N), где:

1. Q – общий объем производства.
2. К – имеющийся капитал.
3. L – человеческие ресурсы (труд).
4. M – сырьевые затраты.
5. Т – используемые технологии.
6. N – талант предпринимателя.

Общей закономерностью, которая применима к данной формуле является то, что объем производства находится в полной зависимости от совокупности всех представленных переменных.

Производственная функция может иметь разный вид, в зависимости от задействованных факторов. Ее упрощают или усложняют, в зависимости от условий, к которым она применима.

Виды экономического понятия

Самыми популярными видами производственных функций считаются:

1. Двухфакторная модель. Считается упрощенной. Определяет зависимость полученного объема товаров от издержек за труд и капитал, поэтому представляется в следующем виде: Q = f (L, K).
2. Функция Кобба-Дугласа. Основывается на постоянных показателях. Указывает на зависимость полученного количества продуктов (промышленных, пищевых) от капитала и трудовых затрат. Представлена в следующем виде: Y = AKaLb, где а и b – константы, которые могут быть представлены только в положительных значениях, A – дополнительные факторы производства. В данную формулу могут быть добавлены различные дополнительные производственные факторы, например, земельные ресурсы (N): Y = AKaLbNy.
3. Формула Леонтьева с фиксированными пропорциями. Заключается в замещении одних ресурсов другими, с постепенным снижением затрат на производство. Имеет следующий вид: Yt = min (AKtBLt), где А и В – внешние параметры производства.

Помимо представленных разновидностей, могут использовать также линейную функцию, которая имеет такой вид – P = aL + bK, где:

• P – полученный продукт;
• a – производительность единицы труда (L);
• b – производительность капитала (K).

На практике используют любую подходящую формулу, каждая из которых сходна между собой по объяснению общих процессов получения продукции. Поэтому производственную функцию относят к уравнениям, характеризующим взаимозависимость между факторами и полученным результатом.

Наглядность характеризующей закономерности

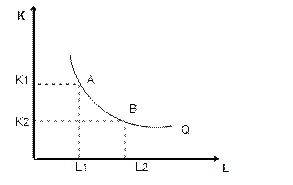
Производственную функцию часто изображают графически, используя для анализа изокванты – прямые, соединяющие все взаимодействующие факторы.

График примерно может выглядеть так, как на этом фото.

Изокванты бывают стандартными и нестандартными, график при этом может выглядеть по-разному, но чаще всего имеет математический вид (основанный на использовании оси координат).

График с изоквантами имеет ряд особенностей:

• чем дальше линия, соединяющая факторы, уходит от нуля, тем больше продукции выпускает предприятие;
• нисходящая линия говорит об уменьшении использовании капитала, что повысит издержки оплаты труда при сохраненном объеме выпуска продукции;
• формы линий зависят от способности замены капитала дополнительными единицами труда (предельными нормами замещения).

Изокванты всегда показывают, какой фактор был больше всего задействован для получения количества продукции – капитал или труд, а также указывает на фиксированные пропорции ресурсов, возможность осуществления действий разными способами, снижение предельной нормы, незавершенность взаимозаменяемости.

Значение понятия для экономики

Производственная функция имеет огромное значение для пояснения экономических процессов в рыночной экономике. Данное понятие в полном объеме характеризует деятельность предприятия, указывая на его доходность и прибыльность, или отсутствие таковых. Главный упор здесь отводится рассмотрению задействованных ресурсов, в их взаимодействии, замене или исключении из общего процесса создания продукта.

Производственная функция относится к полезным, так как она помогает найти наиболее технологические подходы роста прибыли предприятия, повысить все виды эффективности с наименьшими затратами, зафиксировать пропорции сырьевых ресурсов и обеспечить эластичность альтернативных вариантов.

Кроме того, данное понятие определяет предел роста объема выпуска товара, использованные комбинации и физические объемы факторов процесса производства. Это позволит населению потреблять продукты по наименьшей цене. Именно поэтому в экономической науке производственную функцию называют функцией полезности для потребителя.

Источник

Производственная функция. Понятие и виды

ТЕМА 6. ПРОИЗВОДСТВО

Под производством понимается деятельность по использованию факторов производства (ресурсов) с целью достижения наилучшего результата. Если объем использования ресурсов известен, то максимизируется результат и наоборот, если известен результат, которого необходимо достичь, то максимизируется объем ресурсов.

Под затратами понимается все, что фирма (производитель) закупает для дальнейшего использования в целях получения необходимого результата.

Выпуск подразумевает любое благо (продукция или услуга), изготовленное фирмой для продажи. Деятельность фирмы может означать как производственную, так и коммерческую деятельность.

В рамках теории фирмы в целях упрощения представления деятельности принято считать, что фирма производит одно благо.

Поэтому экономическая деятельность фирмы описывается производственной функцией, включающей в себя переменные для выпуска одного вида товара или услуги:

Q – максимальный объем производства при заданных затратах;

В затраты включаются все используемые факторы производства (труд, материалы, оборудование, уровень технико-организационных знаний, при рассмотрении с/х производства учитывается еще один фактор – земля).

При микроэкономическом анализе предполагается, что уровень организационно–технических знаний фиксирован, а все материальные факторы объединяют в один фактор – капитал. Поэтому производственная функция включает в себя два фактора, от которых зависит выпуск продукции: труд и капитал.

Следовательно, производственная функция характеризует техническую зависимость между количеством применяемых ресурсов и максимальным объемом выпуска продукции в единицу времени.

Производственная функция описывает множество технологически эффективных способов производства, каждый из которых характеризуется определенной комбинацией ресурсов, необходимых для получения единицы продукции при данном уровне технологии. Как технологическое соотношение производственная функция может быть определена только эмпирическим путем посредством изменения фактических показателей.

Производственная функция имеет ряд особенностей или свойств:

1) факторы производства являются взаимодополняющими;

2) отсутствие одного из факторов делает производство невозможным;

3) производственная функция, использующаяся на макроуровне, именуется функцией Кобба-Дугласа:

Q = f (k*K a *L b ), где

Q — максимальный объём выпуска продукции;

K — затраты капитала;

L – затраты труда;

a, b — эластичность выпуска по затратам соответствующих факторов (капитала и труда); k – коэффициент пропорциональности или масштабности в отрасли.

4) производственная функция непрерывна и не имеет ограничений по времени, а следовательно, свидетельствует о непрерывности производственного процесса.

Виды производственных функций:

Производственные функции бывают статические и динамические.

Статические производственные функции имеют следующий вид:

Они не включают в себя показатель времени, т.е. не содержат время как фактор, изменяющий основные производственные характеристики изучаемой зависимости.

Среди статических производственных функций наиболее часто встречаются линейные функции (y = a₀ + a₁x₁ + a₂x₂) и функция Кобба-Дугласа.

Динамические производственные функции имеют следующий вид:

x_i (t) – представляет собой динамику изменения определенного производственного фактора в зависимости от времени;

t – представляет собой временную независимую переменную, которая в неявном виде отражает воздействие всех неучтенных факторов на результативность показателя у.

Рассмотрим графическое представление производственной функции. Графиком двухфакторной функции Q = f (L,K) является изокванта, которая представляет собой линию постоянного уровня выпуска. Т.е. изокванта — есть кривая равного продукта или множество возможных комбинаций факторов труда и капитала, при котором достигается один и тот же выпуск продукции.

Рис. 1.6. Двухфакторная производственная функция

Чем дальше от начала координат расположена кривая, тем больше выпуск продукции.

Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный объем выпуска продукции при использовании определенного сочетания факторов производства.

Рис. 2.6. Карта изоквант

К свойствам изоквант относят:

1) отрицательный наклон;

2) вогнутость к началу координат;

3) никогда не пересекаются;

4) показывают различные уровни производства.

Чем дальше от начала координат расположена изокванта, тем больший объем выпуска продукции она показывает.

Источник

Производственная функция

Производственная функция (ПФ) [production function], то же: функция производства — экономико-математическое уравнение, связывающее переменные величины затрат (ресурсов) с величинами продукции (выпуска). ПФ применяются для анализа влияния различных сочетаний факторов производства на объем выпуска в определенный момент времени (статический вариант) и для анализа, а также прогнозирования соотношения объемов факторов и объема выпуска в разные моменты времени (динамический вариант) на различных уровнях экономики — от фирмы (предприятия) до народного хозяйства в целом (агрегированная ПФ, в которой «выпуском» служит показатель совокупного общественного продукта или национального дохода и т.п.). В отдельной фирме, корпорации и т.п. ПФ описывает максимальный объем выпуска продукции, которую они в состоянии произвести при каждом сочетании используемых факторов производства. Она может быть представлена группой изоквант, связанных с различными уровнями объема производства.

Такой вид ПФ, когда устанавливается зависимость объема производства продукции от наличия или потребления ресурсов, называется функцией выпуска.

В частности, широко используются функции выпуска в сельском хозяйстве, где с их помощью изучается влияние на урожайность таких факторов, как, например, разные виды и составы удобрений, методы обработки почвы. Наряду с подобными ПФ используются как бы обратные к ним функции производственных затрат. Они характеризуют зависимость затрат ресурсов от объемов выпуска продукции (строго говоря, они обратны только к ПФ с взаимозаменяемыми ресурсами). Частными случаями ПФ можно считать функцию издержек (связь объема продукции и издержек производства), инвестиционную функцию (зависимость потребных капиталовложений от производственной мощности будущего предприятия) и др.

Математически ПФ могут быть представлены в различных формах — от столь простых, как линейная зависимость результата производства от одного исследуемого фактора, до весьма сложных систем уравнений, включающих рекуррентные соотношения, которыми связываются состояния изучаемого объекта в разные периоды времени.

Наиболее широко распространены мультипликативные формы представления ПФ. Их преимущество состоит в следующем: если один из сомножителей равен нулю, то результат обращается в нуль. Легко заметить, что это реалистично отражает тот факт, что в большинстве случаев в производстве участвуют все анализируемые первичные ресурсы и без любого из них выпуск продукции оказывается невозможным. В самой общей форме (она называется канонической) эта функция записывается так:

или

Здесь коэффициент А, стоящий перед знаком умножения, означает размерность, он зависит от избранной единицы измерений затрат и выпуска. Сомножители от первого до n-го могут иметь различное содержание в зависимости от того, какие факторы оказывают влияние на общий результат (выпуск). Например, в ПФ, которая применяется для изучения экономики в целом, можно в качестве результативного показателя принять объем конечного продукта, а сомножителей — численность занятого населения x₁, сумму основных и оборотных фондов x₂, площадь используемой земли x₃. Только два сомножителя у функции Кобба — Дугласа, с помощью которой была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20-30- гг. ХХ века:

где N — национальный доход, L и K — соответственно, объемы приложенного труда и капитала (подробнее см.: Кобба — Дугласа функция).

Степенные коэффициенты (параметры) показывают ту долю в приросте конечного продукта, которую вносит каждый из сомножителей (или на сколько процентов возрастет продукт, если затраты соответствующего ресурса увеличить на один процент); они называются коэффициентами эластичности производства относительно затрат соответствующего ресурса. Если сумма коэффициентов составляет единицу, это означает однородность функции: она возрастает пропорционально росту количества ресурсов. Но возможны и такие случаи, когда сумма параметров больше или меньше единицы; это показывает, что увеличение затрат приводит к непропорционально большему или непропорционально меньшему росту выпуска (см. Эффект масштаба).

В динамическом варианте применяются разные формы П.Ф. Например (в 2-х-факторном случае): Y(t) = A(t) L a (t) K b (t), где множитель A(t) обычно возрастает во времени, отражая общий рост эффективности производственных факторов в динамике(См. Совокупная факторная продуктивность). Логарифмируя, а затем дифференцируя по t указанную функцию, можно получить соотношения между темпами прироста конечного продукта (национального дохода) и прироста производственных факторов (темпы прироста переменных принято здесь описывать в процентах).

Дальнейшая “динамизация” ПФ может заключаться в использовании переменных коэффициентов эластичности.

Описываемые ПФ соотношения носят статистический характер, т.е. проявляются только в среднем, в большой массе наблюдений, поскольку реально на результат производства воздействуют не только анализируемые факторы, но и множество неучитываемых. Кроме того, применяемые показатели как затрат, так и результатов неизбежно являются продуктами сложного агрегирования (например, обобщенный показатель трудовых затрат в макроэкономической функции вбирает в себя затраты труда разной производительности, интенсивности, квалификации и т.д.).

Особая проблема — учет в макроэкономических ПФ фактора технического прогресса (подробнее см. в статье «Научно-технический прогресс»). С помощью ПФ изучается также эквивалентная взаимозаменяемость факторов производства (см. Эластичность замещения ресурсов), которая может быть либо неизменной, либо переменной (т.е. зависимой от объемов ресурсов). Соответственно функции делят на два вида: с постоянной эластичностью замены, CES (Constant Elasticity of Substi­tution) и с переменной, VES (Variable Elasticity of Substitution) (см. ниже).

На практике применяются три основных метода определения параметров макроэкономических ПФ: на основе обработки временных рядов, на основе данных о структурных элементах агрегатов и о распределении национального дохода. Последний метод называется распределительным.

При построении ПФ необходимо избавляться от явлений мультиколлинеарности параметров и автокорреляции — без этого неизбежны грубые ошибки.

• · Приведем некоторые важные П. ф. (см. также Кобба — Дугласа функция).

Линейная производственная функция:

где a₁, … a_n — оцениваемые параметры модели: здесь факторы производства, замещаемые в любых пропорциях.

Производственнаяфункция CES (constant elasticity of substitution):

P = A [(1 — a) K -в + aL -в ] -c/в ,

в этом случае эластичность замещения ресурсов не зависит ни от K, ни от L и, следовательно, постоянна:

Отсюда и происходит название функции.

Функция CES, как и функция Кобба — Дугласа, исходит из допущения о постоянном убывании предельной нормы замещения используемых ресурсов. Между тем, эластичность замещения капитала трудом и наоборот, в функции К-D равная единице, здесь может принимать различные значения, не равные единице, хотя и является постоянной. Наконец, в отличие от функции K-D, логарифмирование функции CES не приводит ее к линейному виду, что вынуждает использовать для оценки параметров более сложные методы нелинейного регрессионного анализа.

Производственная функция VES (variable elasticity of substitution) (один из вариантов):

P = Ae a t × K a × L b × exp [c (K/L)]

Здесь эластичность замещения принимает различные значения в зависимости от уровня капиталовооруженности труда K/L, откуда и происходит название функции.

См. также: Взаимозаменяемость ресурсов, Изокоста, Изокванта, Изоклиналь, Кобба — Дугласа функция, Коэффициент эластичности производства, Предельная норма замещения, Предельные издержки, Предельный эффект затрат, Предельный продукт, Факторная производительность (продуктивность), Эластичность замещения ресурсов.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело . Л. И. Лопатников . 2003 .

Источник