- Что значит произвольные треугольники
- Треугольник
- Самый произвольный треугольник
- Треугольник
- Треугольник произвольный
- Свойства
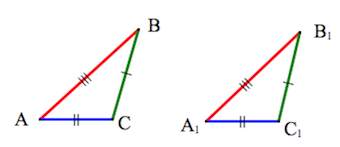
- Признаки равенства треугольников
- Биссектриса, высота, медиана
- Средняя линия треугольника
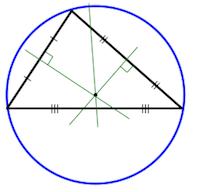
- Вписанная окружность
- Описанная окружность
- Соотношение сторон в произвольном треугольнике
- Площадь треугольника
Что значит произвольные треугольники
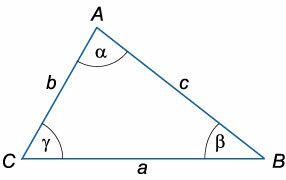
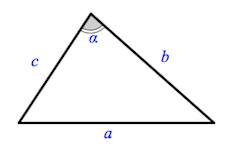
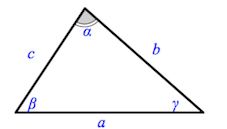
Треугольником называется геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой.
Сумма углов треугольника равна \(180^\circ\):
\(\alpha + \beta + \gamma = 180^\circ\)
Неравенство треугольника
\(a + b > c\)
\(b + c > a\)
\(a + c > b\)
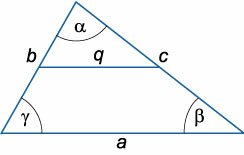
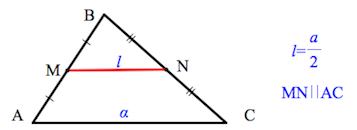
\(\left| \right| Средняя линия треугольника
\(q = a/2,\;\;q\parallel a\)
Радиус описанной окружности
\(R = \large\frac<<\sin \alpha >>\normalsize = \large\frac<<\sin \beta >>\normalsize = \large\frac
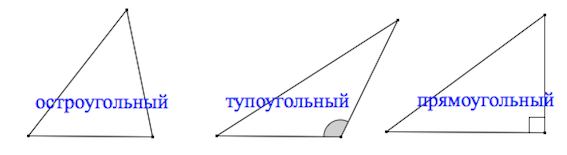
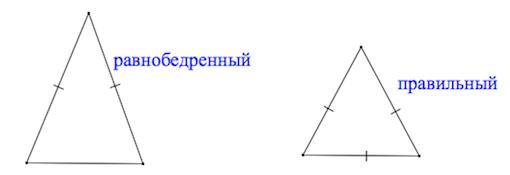
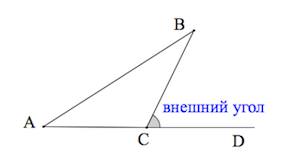
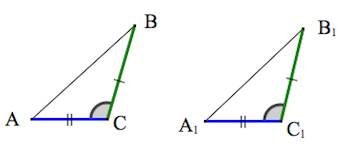
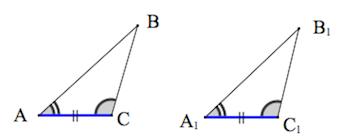
Радиус вписанной окружности \right)\left( \right)\left( \right)>> \normalsize,\;\;\large\frac<1> Нахождение углов треугольника по известным сторонам \right)\left( \right)>>< \right)\left( \right)>> < Нахождение высот треугольника по известным сторонам \right)\left( \right)> \) \right)\left( \right)> \) \right)\left( \right)> \) Нахождение высот треугольника по известной стороне и углу Нахождение медиан треугольника по известным сторонам Расстояния от вершин до центра пересечения медиан Нахождение биссектрис треугольника по известным сторонам \right)>> <<<<\left( \right)>^2>>>\normalsize\) \right)>> <<<<\left( \right)>^2>>>\normalsize\) \right)>> <<<<\left( \right)>^2>>>\normalsize\) Площадь треугольника Источник Рис. 1. Треугольник (общий случай) Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных). В физике эти отрезки классически называются буквами латинского алфавита ( и т.д.), в отличие от обозначений в геометрии. Итак, треугольник, у которого все стороны имеют разную длину и ни один из углов не равен , называется произвольным (рис. 1). В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным. В случае, если у треугольника все стороны одинаковы, он называется равносторонним. В случае, если у треугольника один и углов прямой ( ), он называется прямоугольным. Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами: Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи. Рис. 2. Треугольник (биссектриса) Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями: Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3). Рис. 3. Треугольник (медиана) Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями: Рис. 4. Треугольник (высота) Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4). Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями: Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано. Источник В геометрических задачах от нас часто требуют построить некий произвольный треугольник (как вариант, произвольный прямоугольный, тупоугольный, остроугольный, равнобедренный и т.д.). А так как задача чаще всего даётся без рисунка, то его приходится придумывать самостоятельно. Но как правильно построить этот произвольный треугольник? Рассмотрим два чертежа для задачи с произвольным прямоугольным треугольником. На первом наш треугольник похож на равнобедренный прямоугольный треугольник с одинаковыми катетами. Высота, биссектриса или медиана, проведенные из вершины прямого угла, будут на чертеже неинформативны (по свойству равнобедренного треугольника они будут совпадать). А на втором рисунке гипотенуза по длине похожа на больший катет. Любые построения внутри треугольника будут очень мелкими. Сложно назвать каждый из этих треугольников действительно произвольным в общем смысле. Если проблема всё ещё не очевидна, представьте задачу, которая начинается так: “В треугольнике ABC проведена высота АH и медиана AM. Угол между ними равен 30° . ” Если мы построим треугольник, который будет очень похож на равнобедренный с вершиной А, то по свойству равнобедренного треугольника, высота будет очень близка к медиане. Это затруднит дальнейшую работу с чертежом. Можно, конечно, пытаясь сделать угол похожим на 30°, исхитриться и нарисовать высоту, которая не будет перпендикулярна основанию или медиану, которая не делит противоположную сторону на две части. Однако, это будет существенное расхождение с условием. Чертёж должен помогать нам с решением, а не путать нас. Так как же нарисовать произвольный и, в частности, произвольный прямоугольный треугольник? На самом деле такой способ есть. Многие из вас интуитивно научились строить удобные для решения задач произвольные треугольники. Ниже мы покажем, как именно лучше всего их строить. Опираться мы будем на результаты одноимённой статьи в журнале Квант. Там же указаны обоснования и точные расчёты для наших построений. Итак, перечислим идеальные произвольные треугольники. Обратите внимание, что мы должны учитывать ещё и тип треугольника. Если из условия известно, что он тупоугольный, то это накладывает некоторые ограничения на “произвольность” треугольника . Источник Треугольник – это многоугольник с тремя сторонами (тремя углами). Виды треугольников :+ показать Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚). Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚). Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚). Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием . Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны. 1. Против большей стороны лежит больший угол, и наоборот. 2. Против равных сторон лежат равные углы, и наоборот. 3. Сумма углов треугольника равна 180 º . 4. Внешний угол треугольника равен сумме внутренних углов, (Внешний угол образуется в результате продолжения одной из сторон треугольника). 5. Любая сторона треугольника меньше суммы двух других сторон. 1. Треугольники равны, если у них соответственно равны две стороны и угол между ними. 2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона. 3. Треугольники равны, если у них соответственно равны три стороны. Здесь подробно о биссектрисе, высоте, медиане треугольника. Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника. Средняя линия треугольника параллельна третьей стороне и равна ее половине. Центр вписанной окружности – точка пересечения биссектрис треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров. Теорема косинусов: Теорема синусов: Через две стороны и угол между ними Через радиус описанной окружности Через радиус вписанной окружности Смотрите также площадь треугольника здесь. Чтобы не потерять страничку, вы можете сохранить ее у себя: Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”. Анатолий, спасибо! В разделе свойства: Да, не хватало значка « Здраствуйте! Мне нужна ваша помощь! Подозреваю, у вас опечатка в условии… спасибо я так и думал а то не могу решить и всё Здравствуйте. Пожалуйста, объясните, как решить задачу: Очевидно, Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно Источник
\(
\(\sin \large\frac<\alpha ><2>\normalsize = \sqrt <\large\frac<<\left(
\(\cos\large\frac<\alpha ><2>\normalsize = \sqrt <\large\frac<
\(\tan\large\frac<\alpha ><2>\normalsize = \sqrt <\large\frac<<\left(
\(
\(
\(
\(
\(
\(
\(m_a^2 = \large\frac <<
\(m_b^2 = \large\frac <<
\(m_c^2 = \large\frac <<
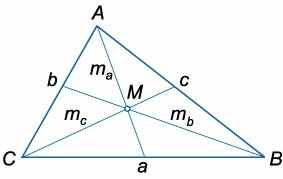
\(AM = \large\frac<2><3>\normalsize
\(t_a^2 = \large\frac <<4bcp\left(
\(t_b^2 = \large\frac <<4acp\left(
\(t_c^2 = \large\frac <<4abp\left(
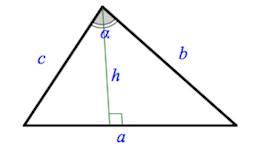
\(S = \large\frac<
\(S = \large\frac<
\(S = pr\)
\(S = \large\frac<
\(S = 2
\(S = Треугольник
Самый произвольный треугольник
Треугольник
Треугольник произвольный
Свойства
не смежных с ним: Признаки равенства треугольников
Биссектриса, высота, медиана
Средняя линия треугольника
Вписанная окружность
Описанная окружность
Соотношение сторон в произвольном треугольнике
Площадь треугольника
, где
– полупериметр
, где
– полупериметр
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!» у А. Спасибо! 😉
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
СПАСИБО!
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти