Что значит прилежащий угол треугольника

Математика

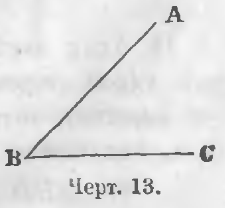
Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.

Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.

Стороны угла. Пересекающиеся линии называются сторонами угла.

Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.

Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.

На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.

Таким образом угол ABC есть угол B или

угол ABC = углу B.

Знак угла. Слово угол заменяют иногда знаком ∠.

Таким образом предыдущее равенство изображают письменно:

В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.

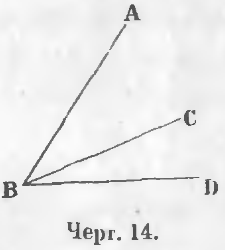
На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.

Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.

Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.

Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14

уг. ABD > уг. ABC и уг. CBD уг. DEF.

c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF

уг. ABC Наклонная линия . Всякая линия неперпендикулярная к другой называется линией наклонною к ней.

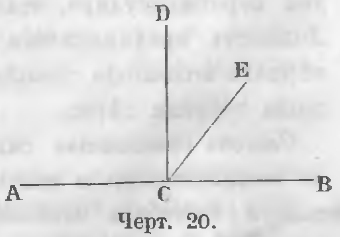
На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.

Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.

Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.

Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.

Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.

Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.

Дана прямая AB и на ней точка C (черт. 20).

Требуется доказать, что можно к ней восставить только один перпендикуляр.

Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра

уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.

Если приложить к первой части последнего неравенства угол ECD, получим неравенство

уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.

Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим

неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.

Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.

Теорема 4. Все прямые углы равны.

Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.

Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.

Заключение. Прямой угол есть величина постоянная.

Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.

В таком случае
всякий острый угол d.

Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.

Теорема 5. Сумма двух смежных углов равна двум прямым.

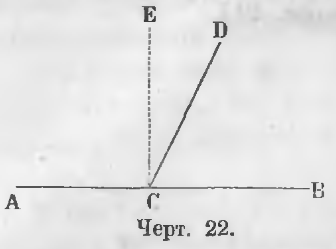
Даны смежные углы ACD и DCB (черт. 22).

Требуется доказать, что ACD + DCB = 2d.

Доказательство. Из точки C восставим перпендикуляр CE, тогда

ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD

Сложив эти равенства, имеем:

ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).

Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.

Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.

Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.

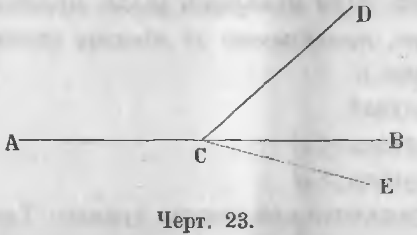
Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).

Требуется доказать, что ACB прямая линия.

Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда

Две величины равные одной и той же третьей равны (аксиома 3), следовательно

ACD + DCB = ACD + DCE

откуда выходит при сокращении

заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).

Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.

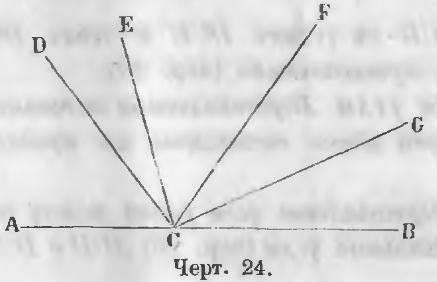
Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).

Требуется доказать, что

ACD + DCE + ECF + FCG + GCB = 2d.

Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).

Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:

ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).

Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.

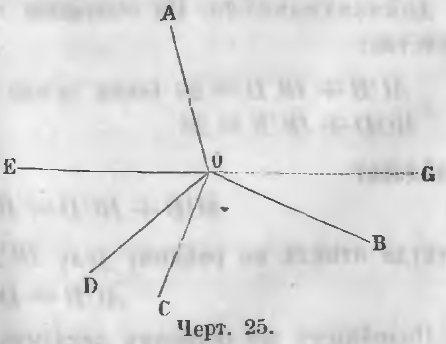
Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).

Требуется доказать, что

AOB + BOC + COD + DOE + EOA = 4d.

Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда

GOB + BOC + COD + DOE = 2d.

Сложив эти равенства, имеем:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Так как AOG + GOB = AOB, то

EOA + AOB + BOC + COD + DOE = 4d (ЧТД).

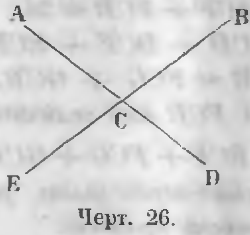
Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).

Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.

Теорема 9. Вертикальные углы равны между собой.

Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.

Требуется доказать, что ACB = DCE и BCD = ACE.

Доказательство. На основании теоремы 5 имеют место равенства:

ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d

ACB + BCD = BCD + DCE

откуда, отняв по равному углу BCD, находим

Подобным же образом доказывают, что

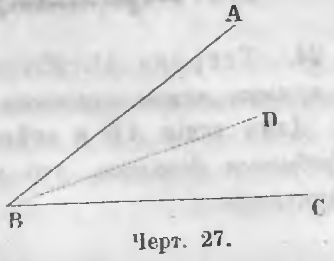
Равносекущая (биссектриса) есть линия, делящая угол пополам.

На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.

Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.

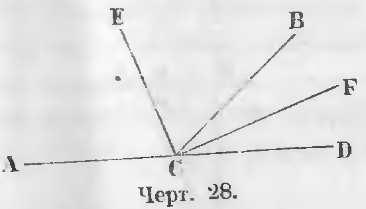
Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.

Требуется доказать, что EC ⊥ CF.

Доказательство. По условию

ECB = ½ ACB, BCF = ½ BCD

Сложив эти равенства, имеем:

ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).

Так как ACB + BCD = 2d, то

ECB + BCF = ½ · 2d = d.

Так как ECB + BCF = ECF, то

Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).

Источник

Треугольники

Определение

Треугольник — это геометрическая фигура, которая состоит из
трех точек, не лежащих на одной прямой и трех отрезков,
соединяющих эти точки.

Точки называются вершинами треугольника.
Отрезки называются сторонами треугольника.

• три угла
• три вершины
• три стороны

Виды углов в треугольнике:

Чтобы лучше понять какие бывают треугольники узнаем
какие бывают углы в треугольниках.

• Острый угол
  Это любой угол меньше 90°.

• Тупой угол
  Это любой угол больше 90°, но меньше 180°.

• Прямой угол
  Это угол 90°.

• Развернутый угол
  Это угол 180°.

Виды треугольников:

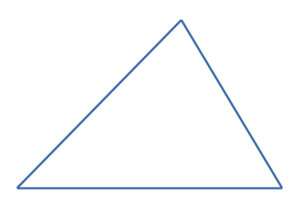
• Острый треугольник
  Это треугольник в котором все углы острые.

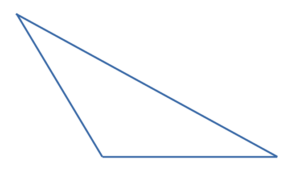
• Тупоугольный треугольник
  Это треугольник в котором один из углов тупой.

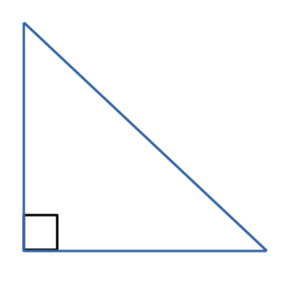
• Прямоугольный треугольник
  Это треугольник в котором один из углов прямой.

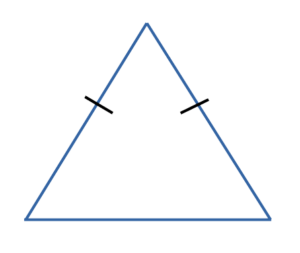
• Равнобедренный треугольник
  Это треугольник в котором две боковые стороны равны.
  
• Равносторонний треугольник
  Это треугольник в котором все стороны равны.
  

Признаки равенства треугольников

С помощью признаков равенства треугольников можно
доказать что те или иные треугольники равны между собой.

Источник

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник