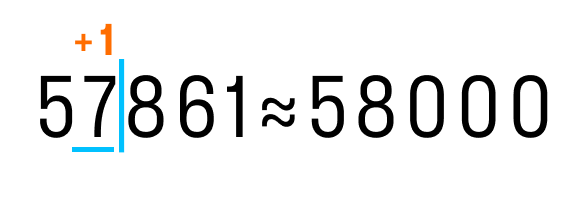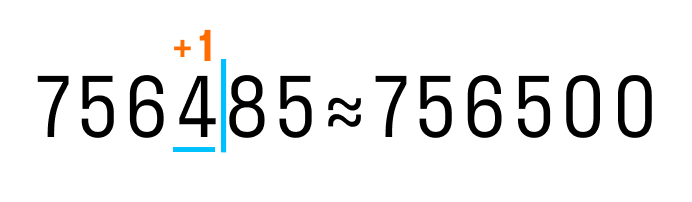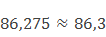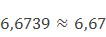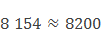Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535. Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213. . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213. то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Источник
Правильное округление чисел
О чем эта статья:
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
- Наименьшее натуральное число: единица (1).
- Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
- У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.
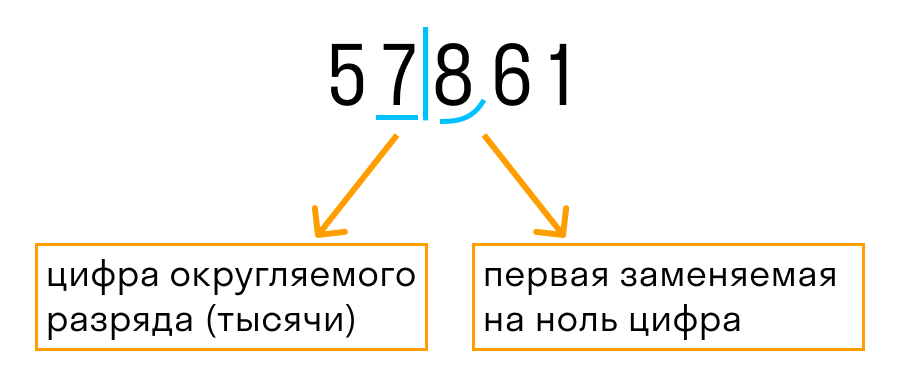
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
- как округлить число 697 до десятков — 697 ≈ 700;
- как округлить число 980 до сотен — 980 ≈ 1000.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
- 7 882 000 = 7 882 тыс.
- 1 000 000 = 1 млн.
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных.
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
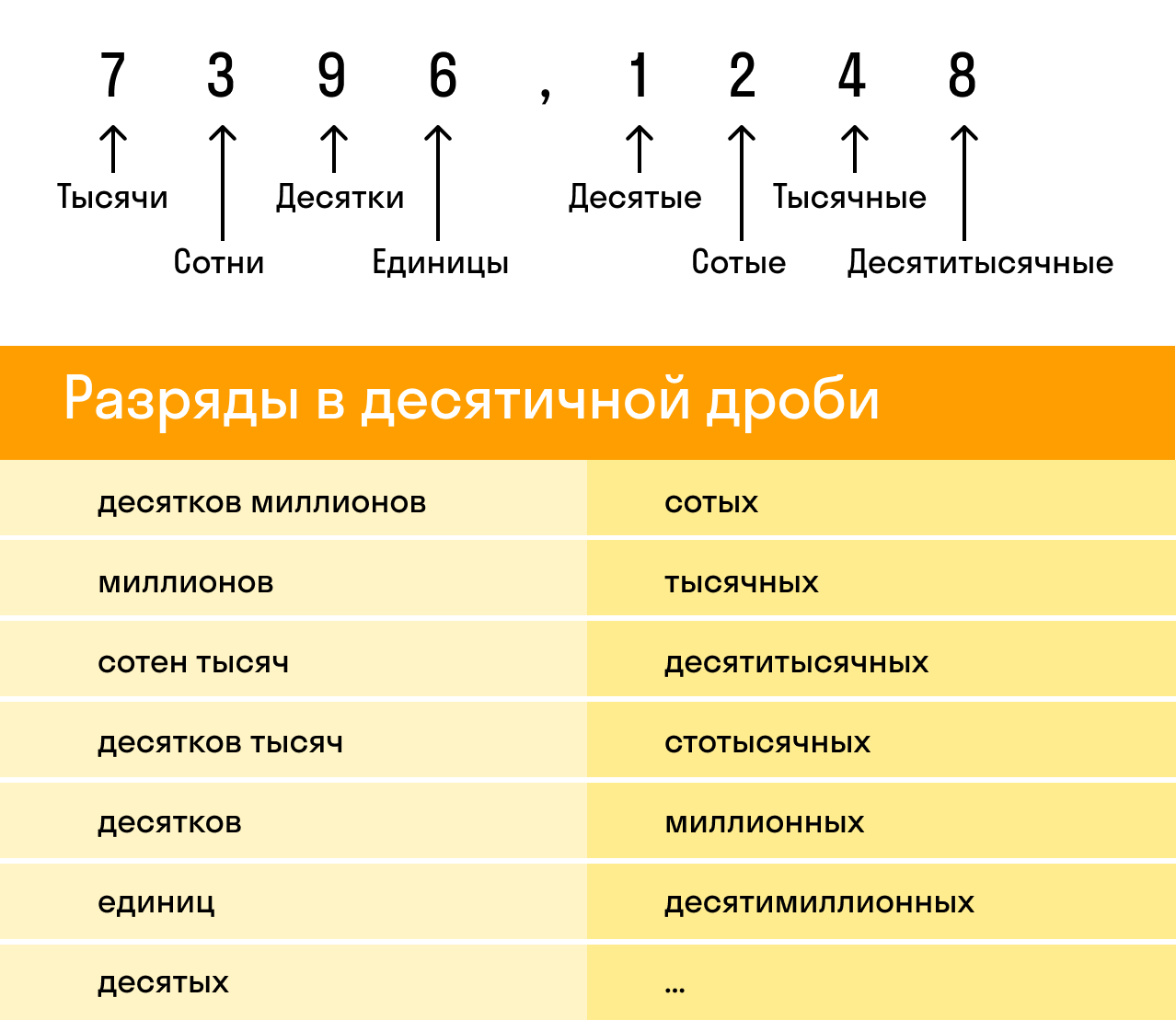
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
- не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
- увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Источник
Что значит приближение числа с недостатком
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
- Главная
- 5-Класс
- Математика
- Видеоурок «Приближенное значение чисел с недостатком и избытком. Округление чисел»
В жизни человека встречается два вида чисел: точные и приближённые.
Например, у квадрата четыре стороны, число 4 является точным.
Другая ситуация, на вопрос, сколько вам лет вы отвечаете 12, это приближенная величина, мы ведь не говорим 12 лет 7 месяцев 26 дней.
На практике мы часто не знаем точных значений величин. Никакие весы, как бы хорошо они ни были настроены, не могут показать абсолютно точный вес. Любой термометр показывает температуру с той или иной погрешностью. Наш глаз не в состоянии увидеть четко показания прибора, поэтому вместо того, чтобы иметь дело с точным значением величины, мы вынуждены оперировать с ее приближённым значением
Однако знание о приближённом числе уже даёт понимание о сути дела, и к тому же не всегда точное значение бывает необходимо.
Приближенные значения чисел в математике разделяют на:
1. приближенные значения с избытком;
2. приближенные значения с недостатком.
Например, про арбуз, который весит 9 кг 280 г, мы можем сказать, что его вес примерно равен 9 кг. Это приближенное значение с недостатком. А если бы его вес составлял 9 кг 980 грамм, мы бы сказали 10 кг – это приближенное значение с избытком.
Другой пример — если длина отрезка равна 25 см 3 мм, то 25 см – это приближенное значение длины отрезка с недостатком, а 26 см – это приближенное значение длины отрезка с избытком.
Итак, если число Х больше числа А, но меньше числа В, тогда А – является приближенным значением числа Х с недостатком, а число В — приближенным значением числа Х с избытком.
Давайте рассмотрим такие примеры:
1)число 58,79 больше чем 58, но меньше 59. Число 58,79 ближе расположено к натуральному числу 59;
2)число 181, 123 больше, чем 181, но меньше, чем 182. Число 181,123 расположено ближе к натуральному числу 181. То натуральное число, к которому дробь ближе называют округленным значением этого числа.
Округление чисел — это математическое действие, которое позволяет уменьшить количество цифр в числе, заменяя его приближенным значением.
Под округлением числа понимают отбрасывание одной или нескольких цифр в десятичном представлении числа. Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Например, число 58,79 округляется до 59, так как число 59 расположено ближе, а число 181,123 округляется до 181.
А что делать, если расстояния до приближенного значения числа с недостатком и избытком равны, например, 23,5? Оказывается, округляют в большую сторону! Т.е. получится 24
Наверняка у вас возник вопрос: «А можно ли округлять не до целого?» Конечно! Округлять можно и до других разрядов, например, до десятых, сотых, тысячных или же до десятков, сотен, тысяч и так далее.
Существует четкое правило для округления чисел:
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если за подчеркнутой цифрой стоит цифра 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.
Теперь стало понятно, почему число 23,5 округлили до 24.
Т.к. отбрасываемая цифра равна 5.
Округлим число 86,275 до десятых.
Подчеркнем цифру 2, отбрасываем цифры 7 и 5, которые следуют за разрядом десятых. За подчеркнутой цифрой 2 стоит цифра 7, поэтому цифру 2 увеличиваем на 1. Получаем 86,3. Записывают это так:
Округлим число 6,6739 до сотых.
Подчеркиваем цифру 7, отбрасываем цифры 3 и 9, которые следуют за разрядом сотых. За подчеркнутой цифрой 7 стоит цифра 3, поэтому цифру 7 оставляем без изменения. Получаем 6,67.
Записывают это так:
Таким образом, можно убедиться, что если десятичную дробь округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры отбрасывают.
Округлим число 8 154 до сотен.
Подчеркиваем цифру 1, за ней следует цифра 5, значит 1 заменяем цифрой 2, а все последующие цифры нулями, то есть получится 8200.
Записывают это так:
Делаем вывод, что при округлении натурального числа до некоторого разряда все цифры последующих разрядов заменяются нулями.
Итак, перед вами несложный алгоритм, который позволяет правильно выполнить округление любого числа:
Первое: найти нужный разряд и подчеркнуть стоящую в нем цифру.
Второе: переписать все цифры, стоящие до нее.
Третье: заменить все цифры, стоящие после выделенной, нулями до конца целой части или отбросить все цифры, имеющиеся после выделенной, если они стоят после запятой.
Четвертое: увеличить выделенную цифру на единицу, если за этой цифрой стоит цифра 5,6,7,8,9 или переписать выделенную цифру без изменений, если за ней стоит цифра 0,1,2,3,4.
Таким образом, в ходе этого урока Вы узнали, что такое приближенные значения чисел с недостатком и избытком округление чисел, а также приобрели четкий алгоритм, который позволяет правильно выполнить округление любого числа!
Источник