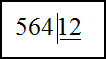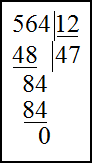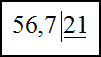Что значит прибавить частное

Значение частного двух чисел в математике

Что такое частное чисел

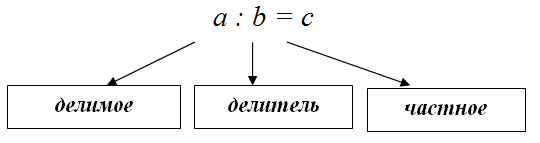
Частное чисел – это результат деления одного числа на другое. Оно показывает, сколько раз число a содержится в числе b.

Деление как операция

Деление – арифметическая операция, обратная умножению, суть которой заключается в нахождении одного из сомножителей по произведению и другому множителю. В данном случае произведение переходит в делимое, имеющийся сомножитель – в делитель, искомый сомножитель – в частное.

Подобно тому, как неоднократно прибавить число – это значит умножить, так и неоднократно вычесть – это значит разделить.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На письме данную операцию можно обозначать разными символами:

• : двоеточием;
• ÷ обелюсом;
• / косой чертой (слеш);
• — горизонтальной чертой (знак дроби).

Процесс деления имеет следующий вид:

В цифрах данное выражение можно записать так:

Основные свойства деления

Деление не коммутативно, то есть не перестановочно – от перемены мест элементов операции частное изменяется:

Деление не ассоциативно – то есть при последовательном выполнении деления трех или более чисел последовательность операций имеет значение, при смене порядка выполнения изменится результат:

Деление дистрибутивно справа – на одном и том же множестве две бинарные операции имеют свойство согласованности:

\((a + b): x = (a : x)+(b : x);\)

Имеется единственный нейтральный элемент – число 1, при делении на единицу результатом является исходное число (делимое):

Имеется единственный обратный элемент – число 1, при делении единицы на число результатом является число, обратное исходному (делителю):

Существует единственный нулевой элемент – число 0, при делении нуля на любое число результатом будет нуль:

Деление на нулевой элемент не определено:

Деление на противоположный элемент дает минус единицу:

Неполное частное

Неполное частное – результат, который получился после деления с остатком.

Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.

Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.

Например, 17 не делится без остатка на 5.

Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.

Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.

Изменение частного в зависимости от изменения делимого и делителя

• увеличение делимого в несколько раз приведет к тому, что частное увеличится во столько же раз:

• уменьшение делимого в несколько раз приведет к тому, что частное уменьшится во столько же раз:

• увеличение делителя в несколько раз приведет к тому, что частное уменьшится во столько же раз:

• уменьшение делителя в несколько раз приведет к тому, что частное увеличится во столько же раз:

Частное не изменится, если делимое и делить одновременно увеличить или уменьшить в одинаковое количество раз:

Задачи, примеры вычисления частного

Для того, чтобы проиллюстрировать данную арифметическую операцию, решим простые задачи.

Задача 1

В книге 891 страница. Она поделена на 9 равных глав. Узнайте, сколько страниц в одной главе.

Для этого количество страниц разделим на количество глав:

891 : 9 = 99 (страниц)

Ответ: 99 страниц.

Задача 2

У Антона есть 22 апельсина. Он хочет приготовить из них компот. Для одного литра компота ему понадобится 3 апельсина. Нужно вычислить, сколько литров напитка сможет приготовить Антон и сколько апельсинов у него останется.

Источник

Что такое частное чисел

Определение частного чисел

Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел $a$ и $b$ будет число $c$, которое равно $c = a : b$ . При этом число $a$ будет делимым, а число $b$ — делителем.

Задание. Найти частное чисел:

1) $39 : 3$ ; 4) $124 : 4$

Ответ. $39 : 3 = 13$

Для нахождения частного больших чисел или десятичных дробей используют способ деления в столбик.

Что такое частное чисел не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Найти частное чисел:

1) $564 : 12$ ; 2) $0,567 : 0,21$

Решение. Для нахождения частного в первом примере выполним деление в столбик. Для этого запишем делимое и делитель следующим образом

Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком. Возьмем по $4 : 4 \cdot 12 = 48$ . Записываем 48 под 56 и находим остаток: $56 — 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.

Таким образом, $564 : 12 = 47$

Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:

Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное. И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 \cdot 21 = 42$ , записываем 42 под 56 и вычитаем: $56 — 42 = 14$ . Остаток 14 списываем к нему следующую незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное, и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.

Таким образом $0,567 : 0,21 = 2,7$

Ответ. $564 : 12 = 47$

Частное рациональных дробей находится по правилу

Задание. Найти частное рациональных дробей:

Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:

Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:

Ответ. $\frac<2><3>: \frac<1><3>=2$

Источник

Что такое частное в математике?

Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.

Деление

В математике есть четыре простейших операции:

Если мы говорим о частном, то нас будет интересовать такая операция, как деление.

Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:

• Двоеточие (:)
• Косая черта (/)
• Обелюс (тире между двумя точками ÷)

В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.

Частное рассказывает, во сколько раз одно число больше другого.

Наглядные примеры

Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.

Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:

a:b=c

Запишем простой пример из математики:

80:2=40

80 – делимое (оно делится)

2 – это делитель (на него разделяют)

Восемьдесят больше, чем сорок, в два раза.

Другой пример выглядит так:

120:2=60

Сто двадцать больше, чем шестьдесят, в два раза.

Проверка

Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:

Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.

Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.

Полное и неполное частное

В результате проведения математических подсчетов частное может быть двух видов:

• Полное. В результате деления мы получаем целое число:

100:2=50

50 – полное частное

• Неполное. Если в результате мы получаем остаток:

51:2=25 (остаток 1)

25 – неполное частное

1 – остаток от деления

Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:

30:6=x

Чтобы найти частное, следует делимое разделить на делитель:

Ответ 5 – это частное в данном примере.

Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.

Источник

Частное в математике — определение, свойства и формула

Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.

Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.

Основное свойство частного

Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.

По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.

Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:

10 — 2 — 2 — 2 — 2 — 2 = 0.

Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:

Частное чисел – это итог процесса деления одного значения на второе. Пример:

где 28 — делимое;

Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:

При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:

Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:

Увеличение или уменьшение делимого

Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.

Изложенное правило имеет такой вид:

12 ⁄ 2 = 6 и пусть n = 3.

Проведём увеличение и уменьшение делимого:

(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;

(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.

То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.

Увеличение или уменьшение делителя

Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:

Для примера требуется взять частное двух значений 54 и 6:

a / b = c и пусть n = 3.

Проведём увеличение и уменьшение делителя:

54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;

54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.

Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.

Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.

Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.

Источник