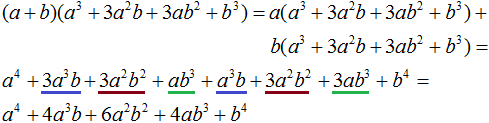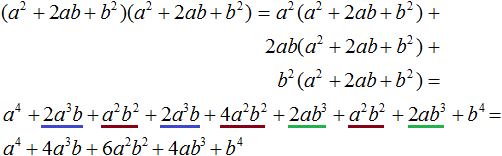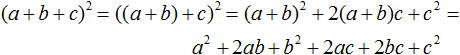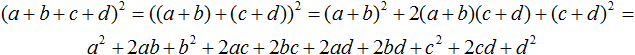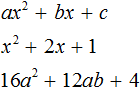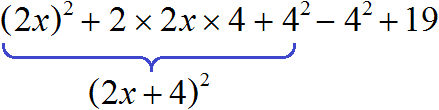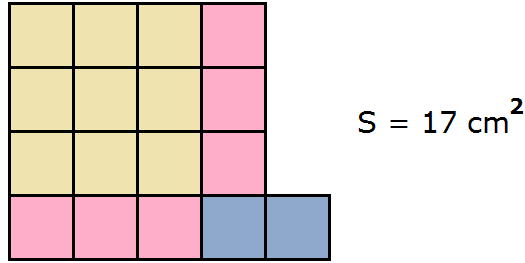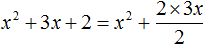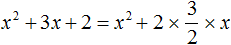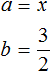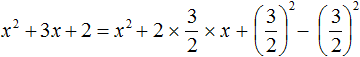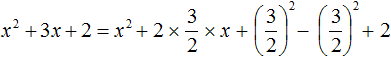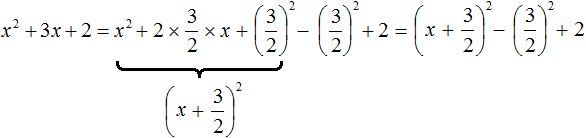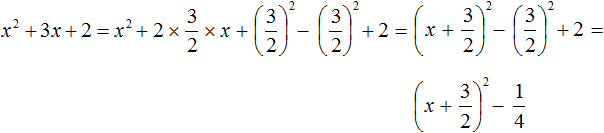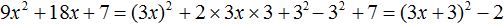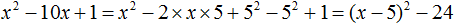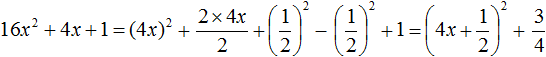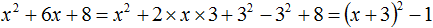Что значит преобразуй многочлен

Учимся приводить многочлены к стандартному виду

В изучении темы о многочленах отдельно стоит упомянуть о том, что многочлены встречаются как стандартного, так и не стандартного вида. При этом многочлен нестандартного вида можно привести к стандартному виду. Собственно, этот вопрос и будем разбирать в данной статье. Закрепим разъяснения примерами с подробным пошаговым описанием.

Смысл приведения многочлена к стандартному виду

Немного углубимся в само понятие, действие – «приведение многочлена к стандартному виду».

Многочлены, подобно любым другим выражениям, возможно тождественно преобразовывать. Как итог, мы получаем в таком случае выражения, которые тождественно равны исходному выражению.

Привести многочлен к стандартному виду – означает замену исходного многочлена на равный ему многочлен стандартного вида, полученный из исходного многочлена при помощи тождественных преобразований.

Способ приведения многочлена к стандартному виду

Порассуждаем на тему того, какие именно тождественные преобразования приведут многочлен к стандартному виду.

Согласно определению, каждый многочлен стандартного вида состоит из одночленов стандартного вида и не имеет в своем составе подобных членов. Многочлен же нестандартного вида может включать в себя одночлены нестандартного вида и подобные члены. Из сказанного закономерно выводится правило, говорящее о том, как привести многочлен к стандартному виду:

• в первую очередь к стандартному виду приводятся одночлены, составляющие заданный многочлен;
• затем производится приведение подобных членов.

Примеры и решения

Разберем подробно примеры, в которых приведем многочлен к стандартному виду. Следовать будем правилу, выведенному выше.

Отметим, что иногда члены многочлена в исходном состоянии уже имеют стандартный вид, и остается только привести подобные члены. Случается, что после первого шага действий не оказывается подобных членов, тогда второй шаг пропускаем. В общих случаях необходимо совершать оба действия из правила выше.

5 · x 2 · y + 2 · y 3 − x · y + 1 ,

0 , 8 + 2 · a 3 · 0 , 6 − b · a · b 4 · b 5 ,

2 3 7 · x 2 + 1 2 · y · x · ( — 2 ) — 1 6 7 · x · x + 9 — 4 7 · x 2 — 8 .

Необходимо привести их к стандартному виду.

Решение

рассмотрим сначала многочлен 5 · x 2 · y + 2 · y 3 − x · y + 1 : его члены имеют стандартный вид, подобные члены отсутствуют, значит многочлен задан в стандартном виде, и никаких дополнительных действий не требуется.

Теперь разберем многочлен 0 , 8 + 2 · a 3 · 0 , 6 − b · a · b 4 · b 5 . В его состав входят нестандартные одночлены: 2 · a 3 · 0 , 6 и − b · a · b 4 · b 5 , т.е. имеем необходимость привести многочлен к стандартному виду, для чего первым действием преобразуем одночлены в стандартный вид:

2 · a 3 · 0 , 6 = 1 , 2 · a 3 ;

− b · a · b 4 · b 5 = − a · b 1 + 4 + 5 = − a · b 10 , таким образом получаем следующий многочлен:

0 , 8 + 2 · a 3 · 0 , 6 − b · a · b 4 · b 5 = 0 , 8 + 1 , 2 · a 3 − a · b 10 .

В полученном многочлене все члены – стандартные, подобных членов не имеется, значит наши действия по приведению многочлена к стандартному виду завершены.

Рассмотрим третий заданный многочлен: 2 3 7 · x 2 + 1 2 · y · x · ( — 2 ) — 1 6 7 · x · x + 9 — 4 7 · x 2 — 8

Приведем его члены к стандартному виду и получим:

2 3 7 · x 2 — x · y — 1 6 7 · x 2 + 9 — 4 7 · x 2 — 8 .

Мы видим, что в составе многочлена имеются подобные члены, произведем приведение подобных членов:

2 3 7 · x 2 — x · y — 1 6 7 · x 2 + 9 — 4 7 · x 2 — 8 = = 2 3 7 · x 2 — 1 6 7 · x 2 — 4 7 · x 2 — x · y + ( 9 — 8 ) = = x 2 · 2 3 7 — 1 6 7 — 4 7 — x · y + 1 = = x 2 · 17 7 — 13 7 — 4 7 — x · y + 1 = = x 2 · 0 — x · y + 1 = x · y + 1

Таким образом, заданный многочлен 2 3 7 · x 2 + 1 2 · y · x · ( — 2 ) — 1 6 7 · x · x + 9 — 4 7 · x 2 — 8 принял стандартный вид − x · y + 1 .

Ответ:

5 · x 2 · y + 2 · y 3 − x · y + 1 — многочлен задан стандартным;

0 , 8 + 2 · a 3 · 0 , 6 − b · a · b 4 · b 5 = 0 , 8 + 1 , 2 · a 3 − a · b 10 ;

2 3 7 · x 2 + 1 2 · y · x · ( — 2 ) — 1 6 7 · x · x + 9 — 4 7 · x 2 — 8 = — x · y + 1 .

Во многих задачах действие приведения многочлена к стандартному виду – промежуточное при поиске ответа на заданный вопрос. Рассмотрим и такой пример.

Задан многочлен 11 — 2 3 z 2 · z + 1 3 · z 5 · 3 — 0 . 5 · z 2 + z 3 . Необходимо привести его к с стандартному виду, указать его степень и расположить члены заданного многочлена по убывающим степеням переменной.

Решение

Приведем члены заданного многочлена к стандартному виду:

11 — 2 3 z 3 + z 5 — 0 . 5 · z 2 + z 3 .

Следующим шагом приведем подобные члены:

11 — 2 3 z 3 + z 5 — 0 . 5 · z 2 + z 3 = 11 + — 2 3 · z 3 + z 3 + z 5 — 0 , 5 · z 2 = = 11 + 1 3 · z 3 + z 5 — 0 , 5 · z 2

Мы получили многочлен стандартного вида, что дает нам возможность обозначить степень многочлена (равна наибольшей степени составляющих его одночленов). Очевидно, что искомая степень равна 5 .

Остается только расположить члены по убывающим степеням переменных. С этой целью мы просто переставим местами члены в полученном многочлене стандартного вида с учетом требования. Таким образом, получим:

z 5 + 1 3 · z 3 — 0 , 5 · z 2 + 11 .

Ответ:

11 — 2 3 · z 2 · z + 1 3 · z 5 · 3 — 0 , 5 · z 2 + z 3 = 11 + 1 3 · z 3 + z 5 — 0 , 5 · z 2 , при этом степень многочлена – 5 ; в результате расположения членов многочлена по убывающим степеням переменных многочлен примет вид: z 5 + 1 3 · z 3 — 0 , 5 · z 2 + 11 .

Источник

Многочлен. Упрощение, степень, стандартный вид, нуль-многочлены

Содержание

Мы с вами уже разобрали, чем являются одночлены, и выяснили, что при произведении одночленов также получится одночлен. Однако совсем иная ситуация обстоит с суммой одночленов. Давайте рассмотрим на примере:

Данные выражения не являются одночленами – в первом у нас представлена сумма одночленов $2a$ и $b^<2>$, а во втором – их разность.

Если данные выражения не являются одночленами, то какое название мы можем им дать? Все просто – такие примеры называют многочленами.

Многочлены – это выражения, которые являются суммой нескольких одночленов.

Упрощение многочленов

Многочлены могут быть как небольшими, так и состоящими из нескольких частей. Давайте рассмотрим несколько примеров таких выражений:

Многочлены состоят из одночленов, которые, в свою очередь, называются членами многочлена. Таким образом, в выражении $11x-2x$ всего 2 одночлена: $11x$ и $-2x$. Многочлены, которые состоят из 2 членов, называются двучленами, а состоящие из 3 – трехчленами. Если в примере содержится обычное число без переменных, то его называют свободным членом многочлена.

В выражениях может находиться несколько подобных членов, что позволяет упростить само выражение. В данном выражении мы можем увидеть подобные одночлены, которые закрашены одинаковыми цветами:

Для упрощения такого многочлена нам нужно использовать правило подобных слагаемых, т.е. произвести отдельные арифметические действия над каждой подобной частью. В конце у нас получится такое выражение:

Такое упрощение называют приведением подобных членов многочлена. Это преобразование позволяет заменить многочлен на тождественно равный ему, но более простой – с меньшим количество членов.

Стандартный вид многочленов

Многочлен, состоящий из одночленов стандартного вида, расположенных в порядке убывания степеней и среди которых нет подобных, называют многочленом стандартного вида.

Одночлены в многочлене стандартного вида располагают в порядке убывания их степени, а свободный одночлен записывают в самом конце. Для примера можно привести следующие выражения:

Стоит отметить, что любой многочлен можно привести к стандартному виду, если привести подобные. То есть из выражения нестандартного вида:

Мы можем получить выражение стандартного вида:

Степень многочлена

Рассмотрим многочлен стандартного вида:

Данное выражение составлено из одночленов: $2x^<3>y$, $-x^<2>y^<2>$, $5x^<2>y$, $y$ и $-2$. Их степени соответственно равны числам $4$, $4$, $3$, $1$, $0$. Наибольшая степень из этих степеней равна числу $4$, поэтому в таком случае говорят, что степень всего многочлена равна $4$.

Степенью многочлена стандартного вида называют наибольшую из степеней одночленов, из которых этот многочлен составлен.

Давайте рассмотрим еще несколько примеров многочленов с их степенями:

$\color3x^<2>-xy+5y^<2>$ – степень равна двум

$\color 3x^<4>y^<2>$ – степень равна шести

$\color 3$ – степень равна нулю

Коэффициенты многочленов

Зачастую многочлен состоит из множества частей, каждая из который имеет свой коэффициент. Они указываются перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена будет равен $1$. Рассмотрим на примере:

Выделенные числа и будут являться коэффициентами переменных множителей.

Нуль-многочлены

Число 0, а также многочлены, которые тождественно равны нулю, называют нуль-многочленами. Примеры таких выражений:

Их не относят к многочленам стандартного вида и считается, что нуль-многочлены не имеют степени.

Источник

Тождественные преобразования многочленов

Возведение двучлена в степень

Двучлен — это многочлен, состоящий из двух членов. В прошлых уроках мы возводили двучлен во вторую и третью степень, тем самым получили формулы сокращенного умножения:

Но двучлен можно возводить не только во вторую и третью степень, но и в четвёртую, пятую или более высокую степень.

К примеру, возведём двучлен a + b в четвертую степень:

Представим это выражение в виде произведения двучлена a + b и куба этого же двучлена

Сомножитель (a + b) 3 можно заменить на правую часть формулы куба суммы двух выражений. Тогда получим:

А это обычное перемножение многочленов. Выполним его:

То есть при возведении двучлена a + b в четвертую степень получается многочлен a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4

Возведение двучлена a + b в четвертую степень можно выполнить ещё и так: представить выражение (a + b) 4 в виде произведения степеней (a + b) 2 (a + b) 2

Но выражение (a + b) 2 равно a 2 + 2ab + b 2 . Заменим в выражении (a + b) 2 (a + b) 2 квадраты суммы на многочлен a 2 + 2ab + b 2

А это опять же обычное перемножение многочленов. Выполним его. У нас получится тот же результат, что и раньше:

Возведение трёхчлена в степень

Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.

Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c

Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:

В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:

Применим эту формулу к нашему примеру:

Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d

Представим многочлен в виде суммы двух выражений: a + b и c + d . Для этого заключим их в скобки:

Теперь воспользуемся формулой квадрата суммы двух выражений:

Выделение полного квадрата из квадратного трёхчлена

Ещё одно тождественное преобразование, которое может пригодиться при решении задач это выделение полного квадрата из квадратного трёхчлена.

Квадратным трехчленом называют трёхчлен второй степени. Например, следующие трехчлены являются квадратными:

Идея выделения полного квадрата из таких трехчленов заключается в том, чтобы представить исходный квадратный трехчлен в виде выражения (a + b) 2 + c , где (a + b) 2 полный квадрат, а c — некоторое числовое или буквенное выражение.

Например, выделим полный квадрат из трёхчлена 4x 2 + 16x + 19 .

Для начала нужно построить выражение вида a 2 + 2ab + b 2 . Строить мы его будем из трехчлена 4x 2 + 16x + 19 . Для начала определимся какие члены будут играть роли переменных a и b

Роль переменной a будет играть член 2x , поскольку первый член трехчлена 4x 2 + 16x + 19 , а именно 4x 2 получается если 2x возвести в квадрат:

Итак, переменная a равна 2x

Теперь возвращаемся к исходному трёхчлену и сразу обращаем внимание на выражение 16x . Это выражение является удвоенным произведением первого выражения a (в нашем случае это 2x ) и второго пока неизвестного нам выражения b . Временно поставим на его место вопросительный знак:

Если внимательно посмотреть на выражение 2 × 2x × ? = 16x , то интуитивно станет понятно, что членом b в данной ситуации является число 4, поскольку выражение 2 × 2x равно 4x , и чтобы получить 16x нужно домножить 4x на 4 .

Отсюда делаем вывод, что переменная b равна 4

Значит, нашим полным квадратом будет выражение (2x) 2 + 2 × 2x × 4 + 4 2

Теперь у нас всё готово для выделения полного квадрата из трёхчлена 4x 2 + 16x + 19 .

Итак, возвратимся к исходному трехчлену 4x 2 + 16x + 19 и попробуем аккуратно внедрить в него полученный нами полный квадрат (2x) 2 + 2 × 2x × 4 + 4 2

Вместо 4x 2 записываем (2x) 2

Далее вместо 16x записываем удвоенное произведение, а именно 2 × 2x × 4

Далее прибавляем квадрат второго выражения:

А член 19 пока переписываем как есть:

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 + 19

Теперь обратим внимание на то, что полученный нами многочлен (2x) 2 + 2 × 2x × 4 + 4 2 + 19 не тождественен изначальному трёхчлену 4x 2 + 16x + 19 . Убедиться в этом можно приведя многочлен (2x) 2 + 2 × 2x × 4 + 4 2 + 19 к стандартному виду:

(2x) 2 + 2 × 2x × 4 + 4 2 + 19 = 4x 2 + 16x + 4 2 + 19

Видим, что получается многочлен 4x 2 + 16x + 4 2 + 19 , а должен был получиться 4x 2 + 16x + 19 . Это по причине того, что член 4 2 был искусственно внедрён в изначальный трёхчлен с целью организовать полный квадрата из трёхчлена 4x 2 + 16x + 19 .

Чтобы сохранить значение исходного многочлена, нужно после прибавления члена 4 2 сразу же вычесть его

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19

Теперь выражение (2x) 2 + 2 × 2x × 4 + 4 2 можно свернуть, то есть записать в виде (a + b) 2 . В нашем случае получится выражение (2x + 4) 2

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19

Оставшиеся члены −4 2 и 19 можно сложить. −4 2 это −16 , отсюда −16 + 19 = 3

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19 = (2x + 4) 2 + 3

Значит, 4x 2 + 16x + 19 = (2x + 4) 2 + 3

Пример 2. Выделить полный квадрат из квадратного трёхчлена x 2 + 2x + 2

Сначала построим выражение вида a 2 + 2 ab + b 2 . Роль переменной a в данном случае играет x, поскольку x 2 = x 2 .

Следующий член исходного трёхчлена 2x перепишем в виде удвоенного произведение первого выражения (это у нас x ) и второго выражения b (это будет 1).

Если b = 1 , то полным квадратом будет выражение x 2 + 2x + 1 2 .

Теперь вернёмся к исходному квадратному трёхчлену и внедрим в него полный квадрата x 2 + 2x + 1 2

x 2 + 2x + 2 = x 2 + 2x + 1 2 − 1 2 + 2 = (x + 1) 2 + 1

Как и в прошлом примере член b (в данном примере это 1) после прибавления сразу был вычтен с целью сохранения значения исходного трёхчлена.

Рассмотрим следующее числовое выражение:

Значение этого выражения равно 17

Попробуем выделить в этом числовом выражении полный квадрат. Для этого сначала построим выражение вида a 2 + 2ab + b 2 . Роль переменной a в данном случае играет число 3 , поскольку первый член выражения 9 + 6 + 2 , а именно 9 можно представить как 3 2 .

Второй член 6 представим в виде удвоенного произведения первого члена 3 и второго 1

То есть переменная b будет равна единице. Тогда полным квадратом будет выражение 3 2 + 2 × 3 × 1 + 1 2 . Внедрим его в исходное выражение:

3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2

Свернем полный квадрат, а члены −1 2 и 2 слóжим:

3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1

Получилось выражение (3 + 1) 2 + 1 , которое по прежнему равно 17

(3 + 1) 2 +1 = 4 2 + 1 = 17

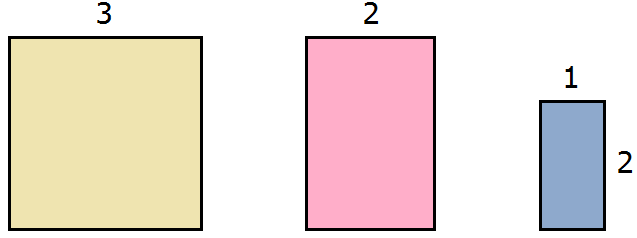
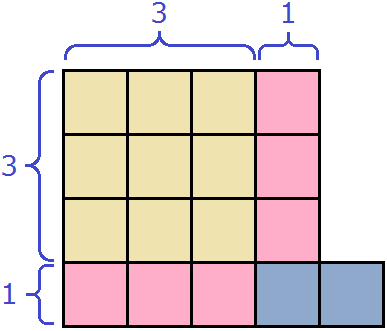
Допустим, у нас имеются квадрат и два прямоугольника. Квадрат со стороной 3 см, прямоугольник со сторонами 2 см и 3 см, а также прямоугольник со сторонами 1 см и 2 см

Вычислим площадь каждой фигуры. Площадь квадрата будет составлять 3 2 = 9 см 2 , площадь розового прямоугольника — 2 × 3 = 6 см 2 , площадь сиреневого — 1 × 2 = 2 см 2

Запишем сумму площадей этих прямоугольников:

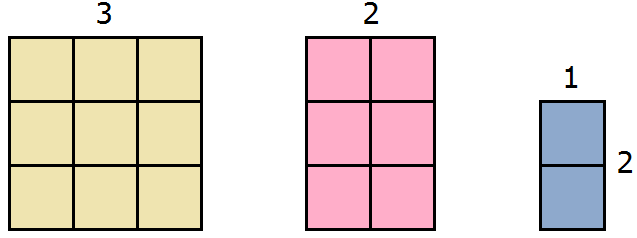
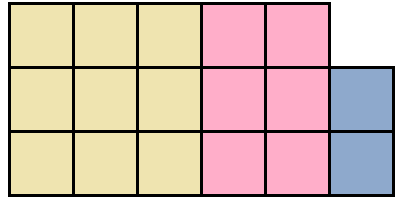
Это выражение можно понимать как объединение квадрата и двух прямоугольников в единую фигуру:

Тогда получается фигура, площадь которой 17 см 2 . Действительно, в представленной фигуре содержится 17 квадратов со стороной 1 см.

Попробуем из имеющейся фигуры образовать квадрат. Причем максимально большой квадрат. Для этого будем использовать части от розового и сиреневого прямоугольника.

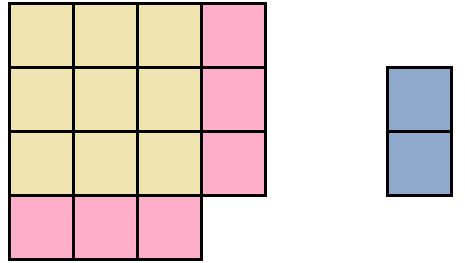
Чтобы образовать максимально большой квадрат из имеющейся фигуры, можно желтый квадрат оставить без изменений, а половину от розового прямоугольника прикрепить к нижней части желтого квадрата:

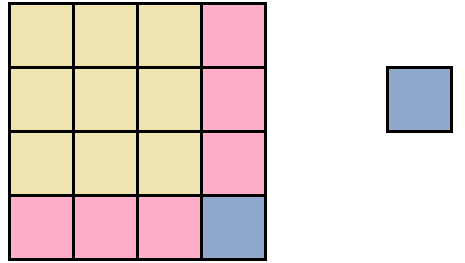
Видим, что до образования полного квадрата не хватает еще одного квадратного сантиметра. Его мы можем взять от сиреневого прямоугольника. Итак, возьмем один квадрат от сиреневого прямоугольника и прикрепим его к образуемому большому квадрату:

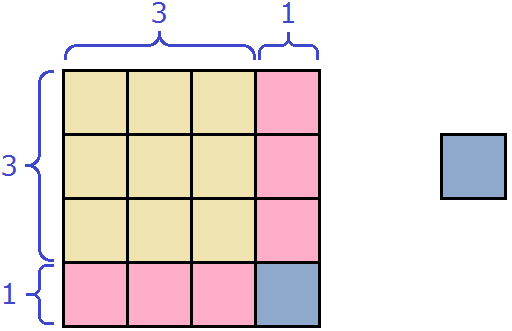
Теперь внимательно посмотрим к чему мы пришли. А именно на желтую часть фигуры и розовую часть, которая по сути увеличила прежний жёлтый квадрат. Не означает ли это то, что была сторона квадрата равная 3 см, и эта сторона была увеличена на 1 см, что привело в итоге к увеличению площади?

(3 + 1) 2

Выражение (3 + 1) 2 равно 16 , поскольку 3 + 1 = 4 , а 4 2 = 16 . Этот же результат можно получить, если воспользоваться формулой квадрата суммы двух выражений:

(3 + 1) 2 = 3 2 + 6 + 1 = 9 + 6 + 1 = 16

Действительно, в образовавшемся квадрате содержится 16 квадратов.

Оставшийся один квадратик от сиреневого прямоугольника можно прикрепить к образовавшемуся большому квадрату. Ведь речь изначально шла о единой фигуре:

(3 + 1) 2 + 1

Прикрепление маленького квадратика к имеющемуся большому квадрату описывается выражением (3 + 1) 2 + 1 . А это есть выделение полного квадрата из выражения 9 + 6 + 2

9 + 6 + 2 = 3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1

Выражение (3 + 1) 2 + 1 , как и выражение 9 + 6 + 2 равно 17 . Действительно, площадь образовавшейся фигуры равна 17 см 2 .

Пример 4. Выполним выделение полного квадрата из квадратного трёхчлена x 2 + 6x + 8

x 2 + 6x + 8 = x 2 + 2 × x × 3 + 3 2 − 3 2 + 8 = (x + 3) 2 − 1

В некоторых примерах при построении выражения a 2 + 2ab + b 2 не бывает возможным сразу определить значения переменных a и b .

Например, выполним выделение полного квадрата из квадратного трёхчлена x 2 + 3x + 2

Переменной a соответствует x . Второй член 3x нельзя представить в виде удвоенного произведения первого выражения и второго. В этом случае второй член следует умножить на 2, и чтобы значение исходного многочлена не изменилось, сразу же выполнить деление на 2. Выглядеть это будет так:

Получившаяся дробь 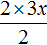и содержит значения переменных a и b . Наша задача суметь правильно их распознать. Перепишем эту дробь в виде произведения множителя 2 , дроби и переменной x

Теперь второй член представлен в виде удвоенного произведения первого выражения и второго. Переменная a , как было сказано ранее, равна x . А переменная b равна дроби

Возвращаемся к нашему примеру и прибавляем квадрат второго выражения, и чтобы значение выражения не изменилось, сразу же вычитаем его:

Прибавляем оставшийся член 2

Свернём полный квадрат:

Оставшийся квадрат второго выражения и число 2 можно сложить. В итоге получим:

Пример 6. Выполним выделение полного квадрата из квадратного трёхчлена 9x 2 + 18x + 7

Пример 7. Выполним выделение полного квадрата из квадратного трёхчлена x 2 − 10x + 1

В данном трёхчлене первые два члена связаны знаком «минус». В этом случае как и раньше нужно выделить полный квадрат, но это будет квадрат разности. Проще говоря, нужно построить выражение вида a 2 − 2ab + b 2 .

Пример 8. Выполним выделение полного квадрата из квадратного трёхчлена 16x 2 + 4x + 1

Пример 9. Разложить многочлен x 2 + 6x + 8 на множители при помощи выделения полного квадрата.

Сначала выделим полный квадрат:

Получившийся многочлена (x + 3) 2 − 1 является разностью квадратов, поскольку единица может быть представлена в виде 1 2 . Воспользуемся формулой разности квадратов и разложим многочлен (x + 3) 2 − 1 на множители:

Источник