Что значит правильный десятиугольник

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

6. Найдите угол правильного десятиугольника (вар. 52)

Найдите угол правильного десятиугольника.

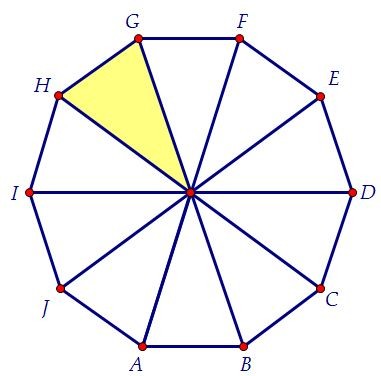
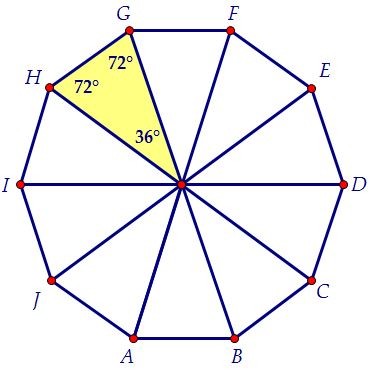
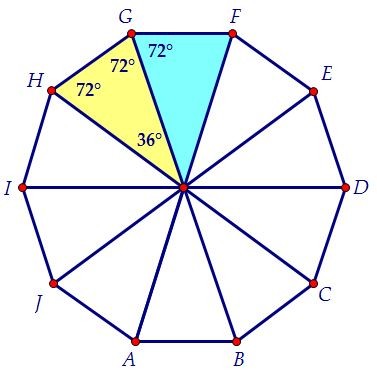
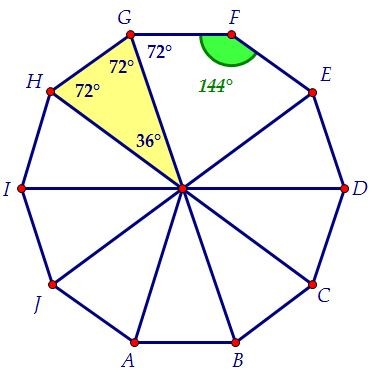
Сначала решим задачу простыми методами. Разобьём правильный десятиугольник на десять равнобедренных и равных друг другу треугольников. Чтобы найти угол при вершине такого треугольника, поделим 360° на 10. Углы при основании равнобедренного треугольника равны. (180° — 36°) : 2 = 72°. В соседнем равнобедренном треугольнике история, разумеется, повторится. Угол правильного десятиугольника состоит из двух углов, равных 72°. Ответ: 144°. Решение для тех, кто любит формулы. Сумма углов правильного n-угольника 180°(n — 2). Найдём сумму углов правильного десятиугольника: 180°(10 — 2) = 180° · 8 = 1440°. Теперь учтём, что у правильного многоугольника все углы равны. 1440° : 10 = 144°. Можно получить ещё больше удовольствия, подставляя число 10 сразу в формулу нахождения угла правильного n-угольника:

Автор: Ольга Себедаш Просмотров: 124930

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

Комментарии к этой задаче:

Комментарий добавил(а): Алина
Дата: 2014-02-16

Комментарий добавил(а): )))
Дата: 2014-02-22

Комментарий добавил(а): Александр
Дата: 2014-06-27

Кстати, треугольник с углами 36 36 и 72 — «золотой». Его бедро относится к основанию как число Ф (золотое сечение, оно равно 1,6180.. — это константа, не менее важная, чем число Пи (pi = 3.14.. или число Эйлера (e = 2,718281828..), если его основание — это сторона правильного пятиугольника. Поэтому то пентаграмма самый что ни на есть «магический» знак, с древности привлекавший множество умов 🙂

Комментарий добавил(а): Анастасия
Дата: 2014-04-19

Спасибо большое!Очень помогли 🙂

Комментарий добавил(а): Дэми
Дата: 2015-04-07

Александр няшность сказал.

Комментарий добавил(а): Полат Алендар
Дата: 2015-10-13

Комментарий добавил(а): Вика
Дата: 2015-09-06

Комментарий добавил(а): shu uemura
Дата: 2016-05-01

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. Tj3eOI7yW С наступающими Велики Майскими праздниками! )

Комментарий добавил(а): медведь
Дата: 2016-03-11

Комментарий добавил(а):
Дата: 2019-02-19

Комментарий добавил(а):
Дата: 2019-03-01

Комментарий добавил(а):
Дата: 2019-03-01

Комментарий добавил(а): Neooreale
Дата: 2019-09-07

Комментарий добавил(а): KEKW
Дата: 2020-07-26

Комментарий добавил(а): KEKW
Дата: 2020-07-26

Комментарий добавил(а): Andro
Дата: 2020-11-25

Комментарий добавил(а): Dano
Дата: 2020-11-25

Источник

Десятиугольник

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.

В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек . Получающийся многогранник будет ограничен фасетами (гранями размерности n-1, в трёхмерном пространстве это многоугольники) вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Так, например, r <4,3>— спрямлённый куб, т.е. кубооктаэдр.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Источник

Десятиугольник

Правильный десятиугольник
Рёбра и вершины	10
Площадь
Внутренний угол (градусы)	144°

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами.

Площадь правильного десятиугольника вычисляется следующим образом:

Внешние ссылки

• Weisstein, Eric W.Decagon (англ.) на сайте Wolfram MathWorld.
• На Викискладе есть медиафайлы по теме Десятиугольник

Многоугольники
По числу вершин	1-10 Одноугольник • Двуугольник • Треугольник • Четырёхугольник (Дельтоид) • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник 11-20 Одиннадцатиугольник (англ.) • Двенадцатиугольник
Правильные	Выпуклые Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • . • 17-угольник • . • 257-угольник • . • 65537-угольник Звёздчатая форма Звезды (Пентаграмма • Гексаграмма • Октаграмма)
Выпуклые	Планигон
См. также	Теория и практика: Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Десятиугольник» в других словарях:

десятиугольник — декагон Словарь русских синонимов. десятиугольник сущ., кол во синонимов: 3 • декагон (1) • … Словарь синонимов

ДЕСЯТИУГОЛЬНИК — ДЕСЯТИУГОЛЬНИК, десятиугольника, муж. (геом.). Замкнутый многоугольник с десятью сторонами. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

десятиугольник — (10 угольник) … Орфографический словарь-справочник

Десятиугольник — (мат.) Разделяя окружность круга на 10 равных частей, получим десять точек. Если мы соединим точки последовательно одну за другой прямыми линиями, то получим Д., так называемый правильный, вписанный в круг. Если же соединим прямыми линиями точки… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Десятиугольник — м. 1. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. 2. Пространство или предмет такой формы. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

десятиугольник — десятиугольник, десятиугольники, десятиугольника, десятиугольников, десятиугольнику, десятиугольникам, десятиугольник, десятиугольники, десятиугольником, десятиугольниками, десятиугольнике, десятиугольниках (Источник: «Полная акцентуированная… … Формы слов

десятиугольник — десятиуг ольник, а … Русский орфографический словарь

десятиугольник — (2 м); мн. десятиуго/льники, Р. десятиуго/льников … Орфографический словарь русского языка

десятиугольник — а; м. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. Начертить д … Энциклопедический словарь

десятиугольник — а; м. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. Начертить десятиуго/льник … Словарь многих выражений

Источник

Десятиугольник: правильный, неправильный, свойства, примеры

Содержание:

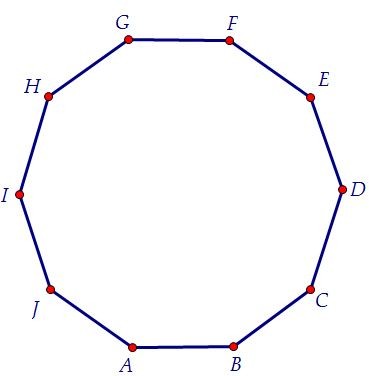
В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Декагоны могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.

На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.

Основными элементами каждого десятиугольника являются:

-Стороны, отрезки линии, которые при соединении образуют десятиугольник.

-Vertices или точки между каждой последовательной стороной.

-Внутренние и внешние углы между соседними сторонами.

-Диагональные, сегменты, соединяющие две непоследовательные вершины.

Вершины названы заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.

Стороны обозначены двумя буквами вершин, между которыми они находятся, например, сторона AB — это сторона между вершинами A и B. То же самое сделано с диагоналями, поэтому у нас есть диагональ AF, которая соединяет точки A и F.

Для углов мы используем этот символ: ∠, похожий на наклонную L. Например, угол ∠ ABC — это угол, вершиной которого является B, а сторонами являются отрезки AB и BC.

Обычный десятиугольник

В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура

Внутренние углы правильного десятиугольника

Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:

-I — мера угла в градусах.

-n — количество сторон многоугольника. В случае десятиугольника n = 10.

Подставляя n = 10 в предыдущую формулу, получаем следующее:

Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, иначе многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.

Сумма внутренних углов

Сумма внутренних углов любого многоугольника в градусах:

S = (n-2) x 180 °; n всегда больше 2

В этой формуле мы имеем:

-S — это сумма размеров внутренних углов.

-n — количество сторон. Для десятиугольника n = 10

Применяя формулу для n = 10, получаем:

S = (10 — 2) x 180º = 1440º

Внешние углы

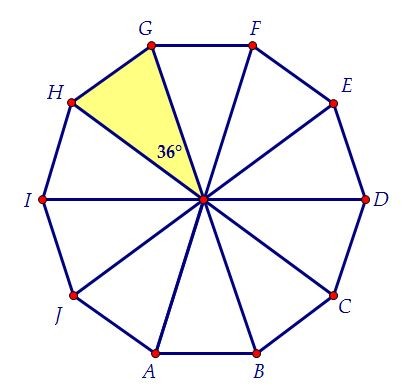
Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:

Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.

Количество диагоналей

Как было сказано ранее, диагонали — это отрезки, соединяющие непоследовательные вершины. Сколько диагоналей мы можем нарисовать в десятиугольнике? Когда количество вершин невелико, их легко сосчитать, но когда это число увеличивается, вы можете потерять счет.

К счастью, есть формула, по которой можно узнать, сколько диагоналей многоугольника. п стороны:

Подставляем десятиугольник n = 10 и получаем:

D = 10 х (10 — 3) / 2 = 35

В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:

Центр

Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.

Периметр

Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:

Площадь

Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:

Приблизительная формула для площади:

И третий способ найти площадь — по длине апофемы L_К. Это сегмент, который соединяет середину одной стороны с центром многоугольника.

В этом случае площадь можно рассчитать по формуле:

Неправильный десятиугольник

Неправильный десятиугольник не является равносторонним или равноугольным, и обычно ему не хватает симметрии правильной фигуры, хотя некоторые десятиугольники могут иметь ось симметрии.

Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.

Неправильный десятиугольник на фиг. 1 вогнут, поскольку некоторые из его внутренних углов больше 180 °. Ясно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.

В любом случае верно, что:

-Внутренние углы неправильного десятиугольника также составляют в сумме 1440º.

-Также имеет 35 диагоналей.

Площадь неправильного десятиугольника по гауссовским определителям

В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:

-Позвоним (х_п , Y_п ) к координатам вершин, причем п варьируется от 1 до 10.

-Вы можете начать с любой вершины, до которой координаты (x₁, Y₁ ). Теперь нам нужно подставить значения каждой координаты в эту формулу:

Где детерминанты — это именно операции в скобках.

-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:

Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. всегда.

Процедура может быть трудоемкой, если у фигуры много вершин, в случае с десятиугольником — 10 операций, поэтому желательно составить таблицу или список.

Упражнение решено

Вычислите площадь неправильного десятиугольника, показанного на рисунке. Координаты вершин — A, B, C… J, значения которых показаны слева.

Решение

-Делаем каждую из 10 операций:

• 2×6 – 4×0 = 12 – 0 =12
• 0×4 – 6×(-2) = 0 + 12 =12
• (-2)×7- 4×(-5) = -14 + 20 = 6
• (-5)×2 – 7×(-6) = -10 + 42 = 32
• (-6)×(-4) – 2×(-4) = 24 + 8 =32
• (-4)×(-2) – (-4)×(-2) = 8 – 8 =0
• (-2)×0 – (-2)×(-1) =0 -2
• (-1)×0 – 0×(2) = 0 – 0 = 0
• 2×2 – 0×8 = 4 – 0 = 4
• 8×4 -2×2 = 32 – 4 = 28

-Давайте добавим результаты:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.

-Предыдущий результат делится на 2, и это площадь многоугольника:

Свойства Десятиугольника

Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:

-У него 10 сторон и 10 вершин.

-Сумма внутренних углов 1440º.

-Есть 35 диагоналей.

-Периметр — это сумма всех сторон.

-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников таким образом, как показано ниже:

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Decagon.com. Декагон. Получено с: decagono.com
3. Открытый справочник по математике. Декагон. Получено с: mathopenref.com.
4. Sangaku Maths. Элементы многоугольника и их классификация. Получено с: sangakoo.com.
5. Википедия. Декагон. Получено с: es.wikipedia.com.

Отрасли экономики Эквадора: основные характеристики

Источник