Что значит положительная автокорреляция

Понятие и причины автокорреляции остатков. Последствия автокорреляции остатков. Обнаружение автокорреляции остатков

Автокорреляции остатков наблюдается тогда, когда значения предыдущих остатков завышают (положительная) или занижают (отрицательная) значения последующих.

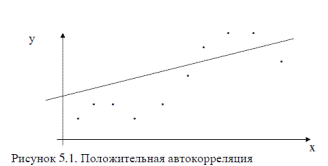
Положительная автокорреляция на графике остатков проявляется в чередовании зон положительных и отрицательных остатков:

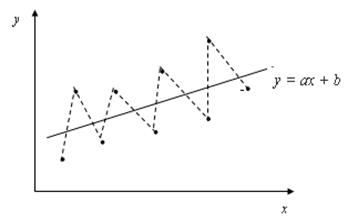
Отрицательная автокорреляция на графике выражается в том, что остатки «слишком часто» меняют знак:

Основными причинами автокорреляции являются:

неправильный выбор формы регрессионной зависимости;

неучет в модели одного или нескольких важных факторов;

цикличность значений экономических переменных при построении модели по временным данным.

Автокорреляция может привести к ошибочному выводу о несущественном влиянии исследуемого фактора на результат Y, в то время как на самом деле влияние фактора на Y значимо.

Для обнаружения автокорреляции остатков используется d-статистика Дарбина–Уотсона:

Значение d-статистики сравнивается с критическими значениями d₁ и d₂. При этом могут возникнуть следующие ситуации:

если , то остатки признаются некоррелированными;

если , то имеется положительная автокорреляция;

если , то существует отрицательная автокорреляция;

если или , то это указывает на неопределенность ситуации.

d‑статистика рассчитывается либо по временному ряду остатков, либо по упорядоченному в зависимости от последовательно возрастающих или убывающих расчетных значений Y.

При неопределенности ситуации рассчитывается коэффициент автокорреляции остатков первого порядка

Автокорреляция отсутствует, если коэффициент не превышает по модулю критическое значение. В противном случае делают вывод о наличие автокорреляции: положительной при или отрицательной при .

Продолжение примера 3. d‑статистика имеет значение d=3,44. Критические значения составляют d₁=0,66 и d₂=1,86 (=0,05; p=3; n=12). d‑статистика попадает в интервал , что свидетельствует об отрицательной автокорреляции остатков.

Коэффициент автокорреляции остатков первого порядка r₍₁₎=–0,721 превышает по модулю критическое значение r_кр=0,576 (=0,05; n=12), что еще раз свидетельствует об отрицательной автокорреляции остатков.

Источник

Сущность и последствия автокорреляции

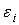
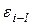
Автокорреляция – это корреляционная зависимость между текущими значениями некоторой переменной и значениями этой же переменной, сдвинутыми на несколько периодов времени назад. Автокорреляция случайной составляющей e модели – это корреляционная зависимость текущих и предыдущих значений случайной составляющей модели. Величина l называется запаздыванием, сдвигом во времени или лагом.

Автокорреляция случайных возмущений модели нарушает одну из предпосылок регрессионного анализа: условие

Автокорреляция может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результирующей переменной. Во-вторых, в ряде случаев причину автокорреляции следует искать в формулировке модели. Модель может не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается на возмущениях, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени t: автокорреляция обычно встречается при анализе временных рядов.

Постоянная направленность воздействия не включенных в модель переменных является наиболее частой причиной так называемой положительной автокорреляции.

Иллюстрацией положительной автокорреляции может служить следующий пример.

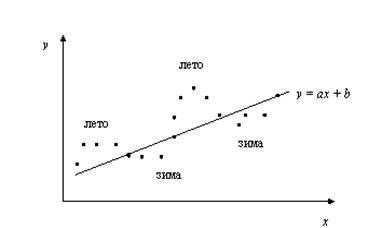
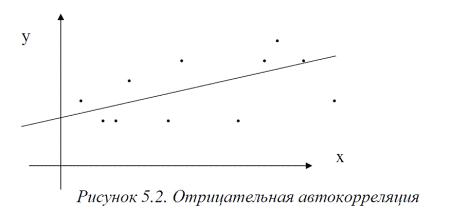
Пример 5.2. Пусть исследуется спрос Y на прохладительные напитки в зависимости от дохода X по ежемесячным и сезонным наблюдениям. Зависимость, отражающая увеличение спроса с ростом дохода, может быть представлена линейной функцией регрессии y = ax + b, изображенной вместе с результатами наблюдений на рис. 5.2.

Рис. 5.2. Положительная автокорреляция

На величину спроса Y оказывают влияние не только доход X (учтенный фактор), но и другие факторы, которые не учтены в модели. Одним из таких факторов является время года.

Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результирующую переменную. Так спрос на прохладительные напитки всегда выше линии регрессии летом (т.е. для летних наблюдений e > 0) и ниже зимой (т.е. для зимних наблюдений e

Рис. 5.3. Отрицательная автокорреляция

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяют следующие.

1. МНК-оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.

2. Стандартные ошибки коэффициентов регрессии будут рассчитываться со смещением. Часто они являются заниженными, что влечет за собой увеличение t-статистик. Это может привести к признанию статистически значимыми объясняющих переменных, которые в действительности таковыми не являются. Смещенность возникает вследствие того, что выборочная остаточная дисперсия 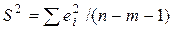(m – число объясняющих переменных модели), которая используется при вычислении указанных величин (см. формулы (2.18) и (2.19)), является смещенной. Во многих случаях она занижает истинное значение дисперсии возмущений s 2 .

Вследствие вышесказанного все выводы, получаемые на основе соответствующих t— и F— статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при проверке качества оценок (параметров модели и самой модели в целом), могут быть ошибочными и приводить к неверным заключениям по построенной модели.

Источник

Автокорреляция. Положительная и отрицательная. Последствия автокорреляции

Кроме проверки значимости коэффициентови качества уравнения регрессии в целом необходима, проверка выполнения условий Гаусса-Маркова, обеспечивающих несмещенность и эффективность оценок параметров регрессии.

Напомним, что при выполнении условия E(ei)=0, i=1,2. n, требование некоррелированности случайных членов cov(ei,ej)=0, i≠j, может быть записано в виде

При нарушении этого условия, т.е. при наличии связи между случайными членами возникает явление автокорреляции. Явление автокорреляции характерно временных рядов, для которых наблюдения жестко упорядочены, и порядок их расположения несет в себе важную информацию.

В случае положительной автокорреляции реализации случайного члена ei для ряда последовательных наблюдений смещают значения зависимой переменной в одном направлении, затем для нескольких последовательных наблюдений – в противоположном направлении, потом снова в первоначальном направлении и т.д.

В экономике положительная автокорреляция может быть связана с циклами деловой активности, с сезонными колебаниями, влияние которых и отражается в случайном члене уравнения регрессии.

При отрицательной автокорреляции каждая реализация случайного члена ei, как правило, сменяется реализаций случайного члена ei+1 противоположного знака.

Для экономики обычно характерно возникновение положительной автокорреляции. Появление автокорреляции более вероятно для малых временных промежутков между наблюдениями.

В случае автокорреляции возмущенной ei ковариационная матрица V(e)=Ω не будет диагональной:

Ω= (s21 s² … s2n) , sij = cov(ei, ej)

Так же как при наличии гетероскедастичности показывается, что оценка вектора коэффициентов β модели множественной линейной регрессии остается несмещенной, но оценка дисперсии возмущенной оказывается смещенной. Значит, все вычисляемые t-статистики коэффициентов будут неправильными, что вполне может привести к неправильным выводам.

Источник

Автокорреляция (Autocorrelation)

Автокорреляция (последовательная корреляция) – сила взаимосвязи Наблюдений (Observation) во Временном ряду (Time Series). Коррелограммы – графики автокорреляции и частичной автокорреляции, широко используются при анализе и прогнозировании временных рядов.

Пример. Используем Датасет (Dataset) минимальных суточных температур за 10 лет (1981–1990) в г. Мельбурн, Австралия. Единицы измерения – градусы Цельсия, всего 3650 наблюдений. Для начала импортируем необходимые библиотеки:

Получим токен Google Cloud SDK, чтобы использовать Google-таблицу:

Загрузим набор данных:

Визуализируем данные, чтобы увидеть сезонные колебания:

График набора данных минимальных суточных температур

Температуры в данном случае – серия Pandas, и создается линейный график временного ряда.

Корреляция и автокорреляция

Статистическая корреляция отображает силу взаимосвязи между двумя переменными.

Мы можем предположить, что распределение каждой переменной соответствует распределению Гаусса (кривая колокола). В этом случае мы можем использовать Коэффициент корреляции Пирсона (Pearson Correlation Coefficient), чтобы суммировать корреляцию между переменными.

Коэффициент корреляции Пирсона – это число от -1 до 1, которое описывает отрицательную или положительную корреляцию соответственно. Нулевое значение указывает на отсутствие корреляции.

Мы можем вычислить корреляцию для наблюдений временного ряда, используя n-ное и (n-1)-е наблюдения. Последние еще называют лагами. Поскольку корреляция наблюдений временного ряда вычисляется со значениями того же ряда в предыдущие моменты времени, это еще называется последовательной корреляцией.

График автокорреляции временного ряда (AutoCorrelation Function – ACF) иногда называют коррелограммой. Давайте построим такой с помощью функции plot_acf() библиотеки statsmodels:

Коррелограмма датасета минимальных суточных температур

При исполнении кода ячейки создается двухмерный график, демонстрирующий корреляцию между двумя временными рядами – исходным и сдвинутым на один день назад. Мы ограничили количество значений по оси x до 35, чтобы улучшить читаемость графика.

Поскольку температурная разница между 1 и 2-м июля, очевидно, небольшая, то и корреляция будет стремиться к единице (второй столбец графика слева). Но когда мы исследуем разницу температур между 1 июля и 4 августа (35 дней разницы – крайний столбец слева), коэффициент корреляции очевидно будет меньше.

Если вы хотите ознакомиться с пошаговой последовательностью построения графика автокорреляции, посмотрите обучающее видео от Brandon Rohrer.

Пошаговая процедура построения коррелограммы

Доверительные интервалы изображены в виде полупрозрачного голубого конуса. По умолчанию установлен доверительный интервал 95%. Если голубая точка каждого из 35 коэффициентов лежит за пределами этой фигуры, то является статистически значимой единицей.

Частичная автокорреляция

Частичная автокорреляция (Partial Autocorrelation – PACF) – это сводка отношений между наблюдением во временном ряду с наблюдениями на предыдущих временных шагах с удаленными взаимосвязями промежуточных наблюдений. Частичная автокорреляция при лаге k возникает после устранения влияния любых корреляций с более короткими лагами.

Автокорреляция для наблюдения и наблюдения на предыдущем временном шаге состоит как из прямой корреляции, так и из косвенной корреляции. Эти косвенные корреляции являются линейной функцией корреляция наблюдения с наблюдениями на промежуточных временных шагах.

Именно эти косвенные корреляции пытается устранить функция частичной автокорреляции. Построим такой график для нашего температурного датасета:

При выполнении примера создается двухмерный график частичной автокорреляции для первых 50 лагов:

График частичной автокорреляции датасета минимальных суточных температур

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Источник