Что значит подводить под понятие

Формирование УУД на примере «подведение под понятие» в рамках ФГОС

Ларионова Людмила Викторовна

ЧОУ СОШ «Общеобразовательный центр «Школа»

Формирование УУД на примере «подведение под понятие» в рамках ФГОС.

Основная задача, стоящая перед современным учителем, заключается в развитии умственных способностей учащихся. Учитель стремится владеть технологиями обучения, направленными на активизацию познавательной деятельности учеников, требующими от них интеллектуальных усилий и продуктивных действий.

В школьной практике многие учителя добиваются от учеников заучивания определений понятий и требуют знания их основных доказываемых свойств. Часто учащиеся безошибочно воспроизводят понятия, то есть обнаруживают знание его существенных признаков, но применить эти знания на практике не могут, опираются на случайные признаки, выделенные благодаря непосредственному опыту.

Умения «подведение под понятие» и «определение понятия» — одни из самых сложных и необходимых понятий, формируемых в единой зависимости в современном уроке по открытию новых знаний.

При формировании понятий необходимо организовывать деятельность учащихся по усвоению двух основных логических приёмов: подведение под понятие и выведение следствий из факта принадлежности объекта понятию.

Подведение под понятие – распознавание объектов, выделение существенных признаков и их синтез. Н. Ф. Талызина, М. Б. Волович указывают, что для усвоения понятий обязательны такие действия:

1. подведение под понятие;
2. выбор необходимых и достаточных признаков для распознавания объекта;
3. выведение следствий о принадлежности и не принадлежности объекта к понятию.

Эти действия необходимы при усвоении любых понятий.

Наиболее распространенными являются определение понятий через род и видовое отличие. Определение через род и видовое отличие состоит из двух понятий: определяемого и определяющего, а сама операция состоит из двух этапов:

1. Определяемое понятие подводится под более обширное по объему родовое понятие (род);
2. Указывается видовое отличие, т.е. устанавливается признак, отличающий определяемый предмет (вид этого рода) от других видов, входящих в данный род.

Приведем символическое выражение определения через род и видовое отличие в виде формулы A=B+С, где А — определяемое понятие, В+С — определяющее понятие (В — род, с — видовое отличие).

Поделюсь опытом работы формирования УУД, в частности «подведение под понятие», используя фрагмент урока информатики в 7 классе теме «Прикладное программное обеспечение».

Одной из главных задач этого урока было научить применять определение понятия прикладного программного обеспечения и подводить под это понятие все известные ученикам компьютерные программы. В ходе этой работы создать условия для развития метапредметных универсальных учебных действий у учащихся.

При изучении данной темы учащиеся уже знакомы с понятием программного обеспечения, как комплекса установленных на компьютере программ, и классификацией его на 3 основные группы (системное, прикладное и системы программирования).

Мною был применен конкретно-индуктивный метод подведения под понятие, включающий в себя следующие шаги:

• рассмотрение различных объектов как принадлежащих объёму понятия, так и не принадлежащих;
• выявление существенных признаков понятия на основе сравнения объектов;
• введение термина, формулировка определения.

При введении понятия конкретно-индуктивным методом учащиеся понимают мотивы введения, учатся строить определения и понимать важность каждого слова в нём.

На первом шаге, после организационного момента и актуализации знаний, учащимся предлагается просмотреть небольшой видеоролик с узнаваемыми достопримечательностями города под звуковое оформление. Далее учитель предлагает подумать, какие программы понадобились для создания этого видеоролика. Учащимся при необходимости можно напомнить, что фотографии были взяты в сети Интернет, был произведен небольшой фотомонтаж, используемая звуковая дорожка – современная аранжировка известной классической композиции. Ученики предлагают свои варианты. С помощью коллективного мозгового штурма на доске формируется копилка используемых программ.

Разобрав каждый предложенный вариант, совместно приходим к выводу, что многие программы не оказывают существенного влияния на работу компьютера в целом, используются лишь при необходимости для решения конкретных задач.

На следующем шаге уже можно сформировать понятие и подвести его под формулу А=В+С : «Прикладное программное обеспечение –программное обеспечение, которое пользователь использует для решения своих практических задач.»

Итогом данного этапа является формулировка понятия, усвоение же происходит на следующем этапе урока. Усвоить определение понятия означает овладеть действиями распознавания объектов, принадлежащих понятию, выведения следствий из принадлежности объекта понятию, конструирования объектов, относящихся к объёму понятия.

Понятие можно считать сформированным, если учащиеся сразу узнают его в задаче без всякого перебирания признаков, то есть процесс подведения под понятие свёрнут. И здесь важно показать, что определение даётся не ради его самого, а для того, чтобы оно «работало» при решении практических задач.

Источник

Формирование УУД на примере «подведение под понятие» в рамках ФГОС.
статья по теме

Одно из первых математических понятий, с которым ученики встречаются в школе – понятие о числе. Если это понятие не будет усвоено, у учащихся возникнут серьезные проблемы при дальнейшем изучении математики. Задача учителя – обеспечить полное усвоение понятия и подведение под это понятие. Однако в школе данная задача решается не всегда успешно, поэтому есть необходимость поговорить об этом.

Скачать:

Вложение	Размер
statya.docx	24.45 КБ

Предварительный просмотр:

Формирование УУД на примере «подведение под понятие»

МБОУ Русская классическая гимназия №2 г. Томска

Алифоренко Зинаида Ивановна.

Образование – это то, что остаётся, когда мы уже забыли всё, чему нас учили.

Основная задача, стоящая перед учителем математики, заключается в развитии умственных способностей учащихся, а не в заполнении ячеек памяти большим количеством формул и правил. Современный учитель стремится владеть технологиями обучения, направленными на активизацию познавательной деятельности учеников, требующими от них интеллектуальных усилий и продуктивных действий.

Логическое мышление учеников развивается интенсивнее, если создать на уроке атмосферу уважения, поощрять инициативу, стимулировать творчество учащихся, а система развивающих заданий позволит привить интерес к предмету, дает более глубокое и полное понимание изучаемых тем, развивает мышление учащихся.

Одно из первых математических понятий, с которым ученики встречаются в школе – понятие о числе. Если это понятие не будет усвоено, у учащихся возникнут серьезные проблемы при дальнейшем изучении математики. Задача учителя – обеспечить полное усвоение понятия и подведение под это понятие. Однако в школе данная задача решается не всегда успешно, поэтому есть необходимость поговорить об этом.

Умения «подведение под понятие» и «определение понятия» — одни из самых сложных и необходимых понятий, формируемых в единой зависимости в современном уроке по открытию новых знаний. Работа по их формированию целенаправленно и планомерно ведётся в системе УМК БИНОМ.

Подведение под понятие – распознавание объектов, выделение существенных признаков и их синтез.

Действие «подведение под понятие» имеет следующую структуру:

1. Выделение всех свойств, зафиксированных в определении.
2. Установление логических связей между ними.
3. Проверка наличия у объекта, выделенных свойств и их связей.
4. Вывод о принадлежности объекта данному понятию.

Поделюсь опытом работы формирования УУД, в частности «подведение под понятие», используя фрагмент урока математики в 6 классе с применением ЭУМК БИНОМ по теме «Рациональные числа».

Одной из главных задач этого урока было научить применять определение понятия рационального числа и подводить под это определение все известные ученикам числа. В ходе этой работы создать условия для развития метапредметных универсальных учебных действий у учащихся.

1 этап урока — организационный . Его задачей являлась организация урока и подготовка к учебной деятельности. На этом же этапе создана мотивация к учебной деятельности: с помощью просмотра фрагмента фильма и ответов на вопросы создан положительный настрой на урок и готовность работать в парах.

2 этап урока — актуализация опорных знаний . Во время этого этапа активизированы мыслительные операции, познавательные процессы (речь, внимание, память). Происходило это при подготовке к проверке домашней работы и подготовке учащихся к работе в диалоге.

На 3 этапе была определена тема урока : в результате проверки домашнего задания ученикам был поставлен вопрос: с каким новым понятием они встретились при подготовке домашнего задания? Надо это понятие подробнее обсудить? К теме урока ученики определили ключевые понятия, над которыми надо работать. Опираясь на электронные тексты, провели проверку домашнего задания, работая в диалоге. В ходе этой работы ученики вырабатывали умение работать с математическим текстом, умение работать в диалоге, умение правильно излагать свои мысли и умение рефлексии, т.к. они сами называли те мыслительные операции, которые приобрели.

4 этап — этап открытия новых знаний . На данном этапе урока ученики работали в группах, на которые поделились при выполнении домашнего задания. Они выработали, опираясь на электронные тексты, определение рационального числа, обсудили, какие числа попадают под это определение и потренировались подводить под это понятие все известные им числа. А для самых любопытных обсудили вопрос о том, как доказать, что бесконечная периодическая дробь является рациональным числом. Рассмотрели виды рациональных чисел и установили связи между различными подмножествами множества рациональных чисел, опираясь на электронный учебник.

5 этап — домашнее задание . Его ученики записали, предварительно прокомментировав с помощью интерактивной доски.

6 этап урока показал анализ ранее изученного материала и использование его для новых выводов. Ученики вспомнили способы сравнения обыкновенных дробей, опираясь на свои модели «ромашки», которую они построили на доске. Затем ученики осуществили перенос способов сравнения через выдвинутую гипотезу на рациональные числа. Мультфильм о сравнении рациональных чисел помог установить универсальный способ сравнения рациональных чисел.

На заключительном, 7 этапе осуществляли осмысление изученного материала и подведение итогов урока. Еще раз проговорили, какие мыслительные операции использовали на каждом этапе урока. Ученики подвели итог, выясняя, какая пара была самой активной в ходе урока, как оценим свою работу на уроке?

Исходя из задач урока, строилась учебная деятельность учащихся путем формирования универсальных учебных действий, делая упор на формирование познавательного блока УУД: предметных действий и универсальных логических действия:

Формирование предметных УУД :

Знать: определение понятия рационального числа и подведение под это определение всех известных ученикам чисел. Знать способы сравнения рациональных чисел.

Начиная с домашнего задания, где ученики столкнулись с новым понятием, и в этапах урока 3,4 и 6 ученики искали ответы на поставленные вопросы, анализировали, сравнивали, работали с текстом, устанавливали аналогии, строили гипотезы.

Понимать : что все, известные ученикам на данном этапе обучения ,числа являются рациональными.

Уметь : применять определение рационального числа для доказательства того, что все, изученные ранее, числа являются рациональными. Уметь сравнивать обыкновенные дроби. Уметь выполнять сравнение рациональных чисел, повторив сравнение обыкновенных дробей.

Формирование метапредметных УУД :

Урок был построен так, чтобы способствовать возможности усвоения учащимися познавательных, регулятивных и коммуникативных универсальных учебных действий

Общеучебные действия УУД

— извлечение необходимой информации из прочитанных текстов различных жанров;

— определение основной и второстепенной информации ,

умение адекватно , подробно, сжато, выборочно передавать содержание текста;

— свободная ориентация и восприятие текстов художественного, научного, публицистического и официально-делового стилей.

Универсальные логические действия УУД:

анализ объектов с целью выделения признаков (существенных, несущественных);

выбор оснований и критериев для сравнения, классификации объектов;

подведение под понятия , выведение следствий;

установление причинно-следственных связей , построение логической цепи рассуждений.

Рефлексия собственной деятельности. Действие смыслообразования, т. е. установление учащимися связи между целью учебной деятельности и ее мотивом было реализовано на всех этапах урока.

На уроке немаловажную роль отводилась осуществление самоконтроля и самооценки, осознание качества и уровня усвоения. Использование приёмов саморегуляции.

Практическая ценность статьи:

В ходе урока у обучающихся развиваются умения находить нужную информацию, систематизировать её, правильно строить и редактировать устный ответ на поставленный вопрос, проводить сравнительный анализ, выполнять тестовые задания. Также на обобщающем уроке эффективным обучающим приемом является задание обучающимся самостоятельно составить план их действий.

Во время урока были использованы различные формы организации учебной деятельности: групповая, фронтальная и индивидуальная.

Источник

Выведение следствий и подведение под понятие

Первый шаг в формировании этих приемов логического мышления у учащихся — знаком­ство с признаками необходимыми и достаточ­ными. Научить дифференцировать эти признаки не так просто. Нередко даже взрослые думают, что всякий достаточный признак является одно­временно необходимым. Фактически же это не так. Вот пример. Если у человека высокая температура, то все понимают, что он болен. Это означает, что признак «высокая температура» является достаточным для признания человека больным. Однако этот признак вовсе не является необходи­мым, так как есть немало болезней, протекающих без температуры. Следовательно, отсутствие темпе­ратуры не означает отсутствия болезни: человек может быть болен, а температуры у него может не быть.

В исследовании И. П. Калошиной и Г. И. Хари­чевой [4] учащимся седьмых классов были предло­жены специальные задания, выполнение которых предполагает понимание характера признаков — необходимые, достаточные, необходимые и одно­временно достаточные.

Вот одно из этих заданий: «Известна теорема: «Диагонали ромба взаимно перпендикулярны».

Объясните, какая из двух формулировок теоремы справедлива: 1. Если четырехугольник есть ромб, то его диагонали взаимно перпендикулярны. 2. Если диагонали четырехугольника взаимно пер­пендикулярны, то данный четырехугольник есть ромб».

Только 24% учащихся смогли правильно выполнить все предложенные в этом эксперимен­те задания. Приведенное задание верно выполни­ли 50% учащихся (выбрали в качестве правиль­ного первое определение). 26% учащихся ответили, что оба предложенных определения являются правильными. Характерно, что последние учащие­ся вообще не видели разницы в предложенных формулировках. Они считали, что в них говорится об одном и том же, «только слова переставлены местами». Это означает, что они не понимают разницы между признаками необходимыми и до­статочными. Во второй формулировке указанные признаки являются необходимыми для ромба, но они недостаточны для его определения, так как этим требованиям удовлетворяет не только ромб, но и делтоид.

Учащимся восьмых-девятых классов было предложено задание: «Докажите, какие из данных слов — краснота, камни, отцветший, большой, гвоздь, краснеющий — являются прилагательны­ми, а какие не являются». Один из учеников правильно воспроизвел определение прилагатель­ного, но применить его в задании не смог. Вот его ответ: «Надо проверить по вопросу «какой?». Если слово отвечает на вопрос «какой?», тогда оно прилагательное». Экспериментатор обращает внимание ученика на то, что в определении ука­зано еще одно требование: прилагательные обозначают признаки предметов. «Как быть с этим требованием? Может быть, оно лишнее и его можно исключить из определения? Ученик расте­рялся и выполнять задание отказался: «Ну, тогда я не знаю*.

Непонимание разницы между признаками необходимыми и достаточными, необходимыми и одновременно достаточными широко распростра­нено среди учащихся старших классов. Происхо­дит это потому, что ни в одном из,классов, ни в одном из изучаемых предметов эти важные логи­ческие знания не являются объектом специаль­ного усвоения. Вместе с тем указанные виды признаков могут быть усвоены уже в начальной школе. Естественно, ученики при этом должны не заучить определения прйзнаков, а научиться работать с ними, то есть выполнять определен­ные логические приемы мышления.

Прежде всего необходимо научить детей выводить следствия из факта принадлежности предмета к данному понятию. Это действие свя­зано с понятием необходимых свойств предмета. Познакомить с ним можно с помощью хорошо известных учащимся предметой. Например, учи­тель, обращаясь к классу, говорит: «Ребята, я принес карандаш. Он у- меня в портфеле. Вы его никогда не видели. Можете ли вы что-нибудь сказать о нем?» Дети дают разные ответы: одни называют грифель, другие — форму, третьи — корпус, который держит грифель, четвертые — цвет и т. д. Ответы детей анализируются с точки зрения обязательности названного детьми призна­ка. В результате выделяются два признака, без которых не может быть ни одного карандаша: наличие грифеля и корпуса, в котором этот гри­фель закреплен.

После этого учитель говорит, что признаки, которые в обязательном порядке есть у всех предметов данного класса, называются необходимыми. Их отсутствие приводит к тому, что пред­мет оказывается не относящимся к данному классу. Если, например, карандаш не будет иметь корпуса, то он из карандаша превратится в гри­фель.

После этого учащиеся выполняют ряд заданий на выведение необходимых свойств. При этом, естественно, используется и учебный материал. Так, в начальных классах школьники знакомят­ся с понятием «отрезок». Учитель может предло­жить задание: «Известно, что линия является отрезком. Не исследуя свойств этой линии, мы можем утверждать, что эта линия обязательно обладает какими свойствами?» Учащиеся должны указать следующие свойства: а) часть прямой; б) ограничена с двух сторон. Наличие этих свойств вытекает из принадлежности линии к понятию «отрезок прямой».

Графически действие выведения следствий по­казано на рис. 3.

Количество свойств, которые могут быть при этом указаны, зависит от содержания самого понятия и от того, насколько продвинулись учащиеся в его изучении. Так, если учащиеся только еще приступили к изучению понятия «тре­угольник», то они смогут указать лишь те свойства, которые содержатся в определении: а) зам­кнутая фигура; б) состоит из трех отрезков прямой. После изучения всех теорем-, относящих­ся к треугольнику (уже в более старших классах), учащиеся смогут указать ряд дополнительных свойств: сумма внутренних углов равна 180°; сумма двух сторон больше третьей и т. д.

Таким образом, формирование приема выве­дения следствий начинается в младших классах и продолжается во всех последующих.

После знакомства с необходимыми признака­ми вводятся понятия признаков достаточных и признаков необходимых и одновременно до­статочных. Важно показать, что не всякий не­обходимый признак является достаточным. Ошиб­ки учащихся связаны именно с тем, что они с необходимыми признаками действуют как с доста­точными. Например, четырехугольник, имеющий хотя бы два прямых угла, они считают прямо­угольником. Это неверно, ибо такими свойствами обладает и прямоугольная трапеция. И для нее, и для прямоугольника это свойства необходи­мые, но не достаточные.

И наоборот, не всякое достаточное свойство является необходимым, на что уже было указано раньше.

Подведение под понятие.

Теперь мы подошли к действию подведения под понятие. Отнесение любого объекта к тому или иному понятию предполагает наличие у этого объекта признаков данного понятия, достаточных или необходимых и -одновременно достаточных.

Как видим, формированию этого приема пред­шествует усвоение целого ряда логических зна­ний и действий, требующих их использования. Если же этого не сделать, то не будет полноцен­но усвоен прием подведения под понятие.

Что же представляет собой этот прием? Какую конкретную деятельность должен выполнять ученик, чтобы безошибочно подводить предметы под то или иное понятие?

Во-первых, надо научиться выделять понятие, под которое требуется подвести данный объект. (В ранее рассмотренном случае с подведением равностороннего треугольника под понятие «равно­бедренный треугольник» последнее и будет таким понятием.)

Во-вторых, надо установить, при каких усло­виях данный объект может относиться к данному понятию. (В рассмотренном случае — при каких условиях треугольник может быть равнобед­ренным. Этот шаг требует знания определения равнобедренного треугольника и умения выде­лить из этого определения систему необходимых и достаточных признаков.) Ученики не всегда, умея воспроизводить определение, умеют анали­зировать его с этой точки зрения.

В-третьих, надо установить, обладает ли дан­ный объект этими признаками. (В нашем случае — обладает ли равносторонний треугольник при­знаками равнобедренного. Для этого необходимо воспроизвести определение равностороннего треу­гольника, сопоставить данные в нем признаки с требуемыми, чему также надо специально обучать.)

Важно показать учащимся, что они должны учитывать именно всю систему необходимых и достаточных признаков. Типичная ошибка школь­ников состоит в том, что они при подведении заданных объектов под соответствующие понятия учитывают лишь некоторые признаки из числа необходимых и достаточных и поэтому относят к понятию и такие предметы, которые имеют лишь некоторые общие признаки с объектами дан­ного класса.

В одном из опытов, проведенном в московской школе, учащиеся шестого класса безошибочно воспроизводили определение окружности, но когда им предъявили эллипс и замкнутую кривую непра­вильной формы и спросили, можно ли эти фигуры назвать окружностью, они ответили ут­вердительно. Беседа показала, что при распозна­вании окружностей они опираются не на всю совокупность признаков, которые указаны в опре­делении окружности и которые они заучили, а только на замкнутость кривой и наличие во внутренней области точки, которую они называют центром.

Аналогично учащиеся шестых-седьмых классов нередко соглашаются назвать смежными углами любые два угла, составляющие в сумме 180°. Они хорошо знают, что любые смежные углы об­ладают этим свойством, то есть они усвоили, что это свойство является необходимым для всех объектов, относящихся к данному классу пред­метов. Но они его используют и как достаточное: считают, что все объекты, обладающие этим свой­ством, относятся к данному классу предметов. А это уже неверно: таким свойством обладают и объекты, не относящиеся к данному классу. Прямые вертикальные углы также в сумме со­ставляют 180°, а смежными не являются.

В связи с этим особенно важно специально поработать над системой свойств, в совокупности являющихся достаточными для определения объектов данного класса. Обязательно надо пока­зать, что учет только одного из свойств данной системы не позволяет определить объекты одно­значно, так как это свойство может быть общим для предметов разных классов.

Все указанные компоненты приема подведения под понятие связаны с определенными предметными знаниями и специфическими действиями, характерными для данного учебного предмета. Учащиеся, проверяя наличие искомых признаков у данного им объекта, могут использовать различ­ные методы, характерные для математики, химии, русского языка. Но во всех случаях общие тре­бования (проверка наличия определенной системы признаков) задает логика. Логика же задает тре­бования и к оценке полученных результатов.

Эти требования можно сформулировать следую­щим образом.

Предмет относится к данному понятию в том и только в том случае, когда он обладает всей системой необходимых и достаточных признаков. Если предмет не обладает хоть одним из этих признаков, он не относится к данному понятию. Если хоть про один признак ничего не известно, то при наличии всех остальных признаков ответ остается неопределенным: неизвестно, принадле­жит или не принадлежит предмет к данному по­нятию.

Учащиеся, получая задания на подведение объ­ектов под понятия, постепенно усваивают этот важный прием.

При работе с этим приемом особое внимание надо уделить тому случаю, когда ответ неопре­деленный. Этот случай усваивается труднее, чем другие, и при целенаправленной работе. Отсутст­вие указаний о том или ином признаке учащиеся обычно расценивают как отсутствие самого при­знака. Например, в задаче: «Даны две пересе­кающиеся прямые. Будут ли они перпендикуляр­ными?» — учащиеся дают отрицательный ответ. Они мотивируют его тем, что в условии не сказано, пересекаются ли прямые под прямым углом. От­вет неверный, так как в условии в равной мере не ^сказано, что прямые пересекаются не под пря­мым углом. Следовательно, про этот признак мы не получаем никакой информации, что и создав! ситуацию неопределенности: может быть, угол прямой, а может быть, не прямой. Правильный ответ в таких задачах: «Неизвестно».

Говоря о действии подведения под понятие, мы подчеркивали, что объект относится к тому или иному понятию тогда и только тогда, когда обладает всей системой необходимых и одновре­менно достаточных признаков. Но так бывает только при подведении под понятия, где призна­ки связаны союзом «и» (конъюнктивная структу­ра признаков). Кроме них, как мы уже говорили, есть понятия с другой структурой признаков: свя­занных союзом «или» (дизъюнктивная структура признаков). В этом случае правило подведения под понятие другое: для отнесения предмета к данному классу достаточно наличия лишь одного из указанных признаков. Эти два случая подве­дения под понятие необходимо дифференциро­вать. Иначе у учащихся может не сформироваться правильных’ приемов подведения.

Задачи на подведение под понятие с дизъюнк­тивной структурой признаков вызывают у учащих­ся большие трудности. Как мы говорили, они до­ставляют немало хлопот и взрослым, если те не владеют соответствующим приемом. Задачи типа ♦ Я тебе мать, а ты мне не дочь», «У двух зря­чих есть слепой брат, но у него нет братьев» и т. п. нередко относят к головоломкам.

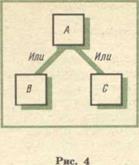
Какой же логический прием подведения под понятие требуется в подобных случаях? Схема­тически характер связей в данной ситуации пока­зан на рис. 4.

Если для понятий с конъюнктивной структу­рой признаков отсутствие хоть одного из них оз­начает непринадлежность предмета к данному понятию, то для понятий с дизъюнктивной структу­рой признаков это не так. Если нет признака В, то мы не имеем права делать отрицательный вывод, а должны обратиться к признаку С. Так, отсутствие дочери не мешает быть матерью — для этого достаточно иметь сына. Усвоив этот прием, учащиеся потом самостоятельно состав­ляют задачи с аналогичным содержанием.

Знакомство с этим приемом можно начать с указанных житейских примеров, а потом уже перейти к учебному материалу. Так, когда уча­щиеся изучают виды предложений, то ряд поня­тий имеет дизъюнктивную структуру признаков. Примером могут служить неполные предложе­ния. Для отнесения предложения к этому поня­тию достаточно одного из двух признаков, соеди­ненных союзом «или»: или нет подлежащего, или нет сказуемого.

Если учителя при усвоении нескольких поня­тий научат школьников логически строго выпол­нять действие подведения под понятие, то в даль­нейшем это действие может успешно использо­ваться при работе с любыми понятиями, имеющи­ми как конъюнктивную, так и дизъюнктивную структуру признаков.

Приемы определения понятий

Уже в начальных классах может быть начата работа над определениями. Но этому должно пред­шествовать усвоение отношений между родовыми и видовыми понятиями. Особое внимание учащих­ся следует обратить на то, что видовое понятие обязательно обладает всеми свойствами родового, а родовое понятие по отношению к видовому вы­ступает как следующая ступень обобщения. Разу­меется, следует при этом еще раз подчеркнуть, что в определение входят только необходимые и одновременно достаточные признаки. Учащимся могут быть показаны и отношения соподчине­ния. Так, в курсе природоведения можно пока­зать, что к лиственным деревьям относятся самые разные виды, а лиственные, в свою очередь, со­подчинены с хвойными: их вместе объединяет понятие «дерево*. Все это помогает заложить ос­нову для формирования более сложных приемов логического мышления.

В настоящее время учащиеся ни в одном из изучаемых в школе предметов не1 знакомятся с логической структурой определения. Они просто заучивают огромное число различных конкретных определений. И если ученик что-то забывает в определении, он не может путем логического рассуждения восстановить забытое, так как не знает структуры определений, не владеет прави­лами их построения.

Поэтому даже в старших классах учащиеся теряются, когда перед ними встает задача оце­нить предложенные определения. Так, в иссле­довании Н. А. Подгорецкой [5] учащимся десятых классов было предложено 20 определений прос­тейших геометрических понятий: ромб, квадрат, прямоугольник, параллелограмм, четырехуголь­ник. Среди определений были как правильные, так и ложные. Учащиеся должны были указать те и другие. Ошибочные определения содержали такие дефекты, как пропуск ближайшего родо­вого понятия, наличие только необходимых при­знаков, неточное указание видовых признаков и т. д. Оказалось, что даже хорошо и отлично успевающие учащиеся в среднем дали 65% пра­вильных ответов. Многие указали как верное та­кое определение параллелограмма: «Параллело­граммом называется четырехугольник, две про­тивоположные стороны которого параллельны». Это определение ошибочное, так как указанные в нем признаки не позволяют отличить паралле­лограмм от трапеции. Определение квадрата как геометрической фигуры, все стороны и все углы которой равны между собой, многие учащиеся также признали правильным. Их не смутило то, что квадрат определяется не через ближайшее ро­довое понятие (прямоугольник), а через весьма отдаленное — «геометрическая фигура».

Видо-родовые отношения понятий, логические правила определений должны войти в программу формирования логического мышления у учащих­ся.

Источник