Что значит плоскость xoy

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

которая эквивалентна уравнению (1).

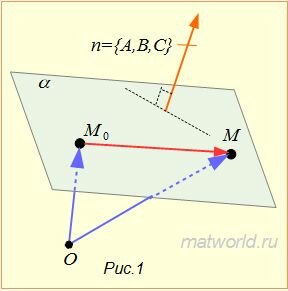Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

.

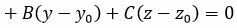Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

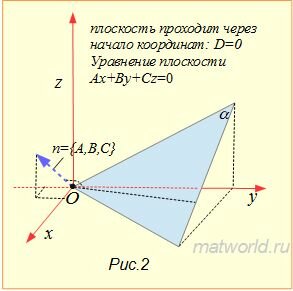
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

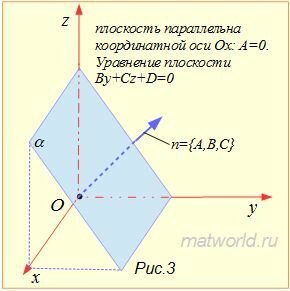
При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

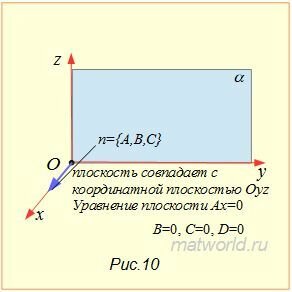
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Источник

Что значит плоскость xoy

2.3.3. йУУМЕДПЧБОЙЕ ПВЭЕЗП ХТБЧОЕОЙС РМПУЛПУФЙ.

рХУФШ РМПУЛПУФШ ЪБДБОБ ПВЭЙН ХТБЧОЕОЙЕН

Ax + By + Cz + D = 0.

чЩСУОЙН, ЛБЛЙЕ ЮБУФОЩЕ РПМПЦЕОЙС ПФОПУЙФЕМШОП ПУЕК ЛППТДЙОБФ ЪБОЙНБЕФ РМПУЛПУФШ, ЕУМЙ ОЕЛПФПТЩЕ ЛПЬЖЖЙГЙЕОФЩ ЬФПЗП ХТБЧОЕОЙС ПВТБЭБАФУС Ч ОПМШ.

1. D = 0. хТБЧОЕОЙЕ РМПУЛПУФЙ РТЙОЙНБЕФ ЧЙД:
   Ax + By + Cz = 0.
   ьФПНХ ХТБЧОЕОЙА ХДПЧМЕФЧПТСЕФ ФПЮЛБ п(0, 0, 0), РПЬФПНХ РМПУЛПУФШ РТПИПДЙФ ЮЕТЕЪ ОБЮБМП ЛППТДЙОБФ.
2. у = 0. хТБЧОЕОЙЕ РМПУЛПУФЙ РТЙНЕФ ЧЙД:
   Ax + By + D = 0.
   Б УБНБ РМПУЛПУФШ РБТБММЕМШОБ ПУЙ OZ.
   бОБМПЗЙЮОП ТБУУХЦДБС, РПМХЮЙН:
   РМПУЛПУФШ РБТБММЕМШОБ ПУЙ OY.
   РМПУЛПУФШ РБТБММЕМШОБ ПУЙ OX
3. D = C = 0. хТБЧОЕОЙЕ РМПУЛПУФЙ РТЙНЕФ ЧЙД:
   Ax + By = 0.
   ьФП ХТБЧОЕОЙЕ РМПУЛПУФЙ, РТПИПДСЭЕК ЮЕТЕЪ ОБЮБМП ЛППТДЙОБФ Й РБТБММЕМШОПК ПУЙ OZ, ФП ЕУФШ ЬФП ВХДЕФ РМПУЛПУФШ, РТПИПДСЭБС ЮЕТЕЪ ПУШ OZ.
   бОБМПЗЙЮОП, ЕУМЙ B = C = 0, ХТБЧОЕОЙЕ РМПУЛПУФЙ ВХДЕФ:
   Ax + D = 0,
   ФП ЕУФШ РМПУЛПУФШ РТПИПДЙФ ЮЕТЕЪ ПУШ OY.
   оБЛПОЕГ, ЕУМЙ A = D = 0, хТБЧОЕОЙЕ РМПУЛПУФЙ ВХДЕФ:
   By + Cz = 0.
   ФП ЕУФШ РМПУЛПУФШ РТПИПДЙФ ЮЕТЕЪ ПУШ OX.
4. еУМЙ ТБЧОЩ ОХМА ДЧБ ЛПЬЖЖЙГЙЕОФБ РТЙ ФЕЛХЭЙИ ЛППТДЙОБФБИ, ФП ХТБЧОЕОЙЕ ПРТЕДЕМСЕФ РМПУЛПУФШ, РБТБММЕМШОХА ЛППТДЙОБФОЩН РМПУЛПУФСН:
   — РМПУЛПУФШ РБТБММЕМШОБ РМПУЛПУФЙ XOY.
   — РМПУЛПУФШ РБТБММЕМШОБ РМПУЛПУФЙ ZOY.
   — РМПУЛПУФШ РБТБММЕМШОБ РМПУЛПУФЙ XOZ.
5. еУМЙ — ЬФП ХТБЧОЕОЙЕ РМПУЛПУФЙ YOZ.
   — ЬФП ХТБЧОЕОЙЕ РМПУЛПУФЙ XOZ.
   — ЬФП ХТБЧОЕОЙЕ РМПУЛПУФЙ XOY.

Источник

Примеры

Пример 1. Покажем, что точка M (1, 2, 10) принадлежит плоскости x − y + 1 = 0 .

Решение. Подставляем координаты точки x = 1 , y = 2 и z = 10 в уравнение плоскости x − y + 1 = 0 . Получаем

1 − 2 + 1 = 0 Ю 0 ≡ 0

Так как уравнение превратилось в тождество, точка M (1, 2, 10) принадлежит плоскости x − y + 1 = 0 .

Пример 2. Найдем точки пересечения плоскости x − y + 1 = 0 с осями координат.

1. Чтобы найти точку пересечения плоскости x − y + 1 = 0 с осью O X , надо решить систему уравнений

y = 0 z = 0 x − y + 1 = 0

Получаем x = −1 , y = 0 , z = 0 .

2. Чтобы найти точку пересечения плоскости x − y + 1 = 0 с осью O Y , надо решить систему уравнений

x = 0 z = 0 x − y + 1 = 0

Получаем x = 0 , y = 1 , z = 0 .

3. Чтобы найти точку пересечения плоскости x − y + 1 = 0 с осью O Z , надо решить систему уравнений

x = 0 y = 0 x − y + 1 = 0

Система не имеет решений. Следовательно, плоскость x − y + 1 = 0 параллельна оси O Z .

Пример 3. Найдем нормальный вектор плоскости x − z + 2 = 0 и опишем ее положение в пространстве относительно координатных осей.

1. В качестве нормального вектора плоскости x − z + 2 = 0 возьмем вектор, координаты которого равны коэффициентам при x , y и z в уравнении плоскости, т.е.

→

n

= <1, 0, −1>.

2. Находим точки пересечения плоскости x − z + 2 = 0 с осями координат, решая соответствующие системы уравнений (см. задачу 2). Получаем точки пересечения: с осью O X ( −2, 0, 0) , с осью O Z (0, 0, 2) , с осью O Y плоскость не пересекается.Следовательно, плоскость x − z + 2 = 0 параллельна оси O Y .

Пример 4. Составим уравнение координатной плоскости X O Y .

Решение. Уравнение плоскости, проходящей через данную точку M ( x 0 , y 0 , z 0 ) перпендикулярно данному вектору

→

n

= < A , B , C >имеет вид

A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0.

(1)

Выберем в качестве нормального вектора плоскости X O Y базисный вектор

→

k

= <0, 0, 1>, а в качестве точки, принадлежащей плоскости X O Y , — начало координат O (0, 0, 0) . Тогда уравнение (1) приобретает вид:

0 ( x − 0) + 0 ( y − 0) + 1 ( z − 0) = 0 Ю z = 0.

Таким образом, уравнение плоскости X O Y : z = 0 .

Пример 5. Найдем углы между плоскостями 2 x + 2 y + z − 1 = 0 и x + z − 1 = 0 .

Решение. Поскольку двугранные углы между плоскостями равны углам между нормальными векторами этих плоскостей (

→

n

1 = <2, 2, 1>и

→

n

2 = <1, 0, 1>), имеем

cos j = ( → n 1 , → n 2 ) | → n 1 | · | → n 2 | = 2 · 1 + 2 · 0 + 1 · 1 √ 2 2 + 2 2 + 1 2 √ 1 2 + 0 2 + 1 2 = 3 3 √ 2 = √ 2 2 .

Таким образом, углы между плоскостями равны π/4 и 3π/4 .

Пример 6. Составим уравнение плоскости, проходящей через три данные точки M (1, 2, 3), N (0, 2, −2) и P ( 3, 1, 0) (рис.1).

1. Пусть Q ( x , y , z ) — произвольная точка пространства. Построим векторы M Q = < x − 1, y − 2, z − 3>, M N = < −1, 0, −5>и M P = <2, −1, −3>. Точка Q принадлежит искомой плоскости тогда и только тогда, когда векторы M Q , M N и M P компланарны.

2. Условие компланарности трех векторов

x −1 y −2 z −3 −1 0 −5 2 −1 −3

= 0 .

3. Разлагая определитель по первой строке, после несложных преобразований получаем уравнение искомой плоскости:

5 x + 13 y − z − 28 = 0 .

Рекомендуем сделать проверку, подставив в уравнение плоскости координаты точек M , N и P .

Источник