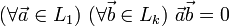Что значит перпендикулярно телу

Перпендикулярность

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Смотреть что такое «Перпендикулярность» в других словарях:

ПЕРПЕНДИКУЛЯРНОСТЬ — (от сл. перпендикуляр). Отвесность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕРПЕНДИКУЛЯРНОСТЬ от слова перпендикуляр. Отвесность. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык,… … Словарь иностранных слов русского языка

перпендикулярность — вертикальность, нормальность, ортогональность Словарь русских синонимов. перпендикулярность сущ., кол во синонимов: 4 • вертикальность (3) • … Словарь синонимов

ПЕРПЕНДИКУЛЯРНОСТЬ — ПЕРПЕНДИКУЛЯРНОСТЬ, перпендикулярности, мн. нет, жен. (мат.). Перпендикулярное положение. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

перпендикулярность — ПЕРПЕНДИКУЛЯРНЫЙ, ая, ое; рен, рна. Являющийся перпендикуляром. Перпендикулярные линии. Расположить перпендикулярно (нареч.) к чему н. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Перпендикулярность — 4.16 Перпендикулярность: а) поверхности 6 к поверхностям 7 и 9; Источник: ГОСТ 2110 93: Станки расточные горизонтальные с крестовым столом. Нормы точности оригинал документа … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности. Содержание 1 На плоскости 1.1 Перпендикулярные … Википедия

Перпендикулярность — ж. Перпендикулярное положение, расположенность под прямым углом к чему либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

перпендикулярность — перпендикулярность, перпендикулярности, перпендикулярности, перпендикулярностей, перпендикулярности, перпендикулярностям, перпендикулярность, перпендикулярности, перпендикулярностью, перпендикулярностями, перпендикулярности, перпендикулярностях… … Формы слов

перпендикулярность — перпендикул ярность, и … Русский орфографический словарь

перпендикулярность — см. перпендикулярный; и; ж. Перпендикуля/рность плоскостей. Перпендикуля/рность расположения предметов … Словарь многих выражений

Источник

Перпендикуляр

Содержание

Перпендикулярность прямых на плоскости

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

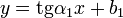
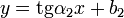
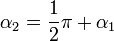
В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . (Здесь α₁,α₂ — углы наклона прямой к горизонтали)

Перпендикулярность прямых в пространстве

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

Построение перпендикуляра на плоскости

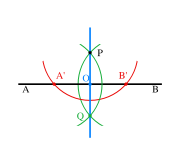
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярность плоскостей в 3-мерном пространстве

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.

• Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
• Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости.
• Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Таких пар 6 (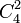): xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство W n , а прямая l с направляющим векторным пространством L 1 и гиперплоскость Π_k с направляющим векторным пространством L k (где , ) принадлежат пространству .

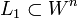
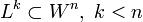
Прямая l называется перпендикулярной гиперплоскости Π_k , если подпространство L₁ ортогонально подпространству L k , то есть

Источник

Значение слова «перпендикулярно»

ПЕРПЕНДИКУЛЯ́РНО. Нареч. к перпендикулярный (во 2 знач.). Когда большая стрелка [часов] станет прямо вверх, а маленькая почти перпендикулярно к ней вправо, то тогда надо ему сменяться. Куприн, Ночная смена.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

перпендикулярно

1. геометр. составляя прямой угол с какой-либо прямой или плоскостью ◆ У большинства планет, включая Землю, ось вращения расположена почти вертикально, то есть перпендикулярно к плоскости орбиты планеты. Георгий Бурба, «Открытый дважды», 15 июня 2004 г. // «Вокруг света» (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: погончик — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «перпендикулярно&raquo

Синонимы к слову «перпендикулярно&raquo

Предложения со словом «перпендикулярно&raquo

• Ход ствольной коробки ограничивается ствольной задержкой, кривошип поворачивается до своего крайнего заднего положения – почти перпендикулярно оси канала ствола.

Цитаты из русской классики со словом «перпендикулярно»

• В нижнем течении Лефу принимает в себя с правой стороны два небольших притока: Монастырку и Черниговку. Множество проток и длинных слепых рукавов идет перпендикулярно к реке, наискось и параллельно ей и образует весьма сложную водную систему. На 8 км ниже Монастырки горы подходят к Лефу и оканчиваются здесь безымянной сопкой в 290 м высоты. У подножия ее расположилась деревня Халкидон. Это было последнее в здешних местах селение. Дальше к северу до самого озера Ханка жилых мест не было.

Понятия, связанные со словом «перпендикулярно»

Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).

Источник

Перпендикулярность

Содержание

На плоскости

Перпендикулярные прямые

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . Эти же прямые будут перпендикулярны, если . (Здесь — углы наклона прямой к горизонтали)

Для обозначения перпендикулярности имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

Построение перпендикуляра

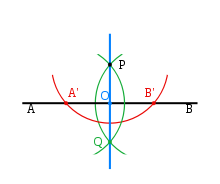
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).

Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.

Во всех остальных случаях

xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.

В трёхмерном пространстве

Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

• Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
• Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
• Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
• Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения [1] .

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством и гиперплоскость с направляющим векторным пространством (где , ) принадлежат пространству .

Прямая l называется перпендикулярной гиперплоскости , если подпространство ортогонально подпространству , то есть

Источник