Что значит пересечение отрезков

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

На рисунке изображена прямая a и точки D, F, G и H . Точки F и G лежат на прямой a . Точки D и H не лежат на прямой a .

В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.

Задача № 1 из учебника Атанасян 7-9 класс

Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .

Решение задачи

Обозначим её буквой a .

Отметим точки (·)A и (·)B , лежащие на прямой a .

Отметим точки (·)P, (·)Q и (·)R , не лежащие на прямой a .

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

На рисунке прямые a и b не пересекаются . Прямые b и c пересекаются .

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

В тексте пересечение прямых обозначают символом ∩ . Информацию на рисунке выше можно записать следующим образом:

• b ∩ c — прямые b и с пересекаются;
• a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M . Другими словами, прямые пересекаются в точке M . Геометрическими обозначениями пересечение прямых в точке записывается так:
e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через любые две точки можно провести прямую, и притом только одну .

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M .

Третий случай расположения прямых

Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B .

Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно .

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Теперь прямая a пересекается с прямой b , прямая b пересекается с прямой c и прямая c пересекается с прямой a .

В этом случае у нас только одна точка пересечения всех прямых — точка (·)D .

Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D . Тогда получится три точки пересечения — (·)D, (·)E и (·)F .

Прямая a пересекается с прямой b в точке (·)D , прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E . Условие задачи выполнено.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T .

Сам отрезок можно назвать ST или TS . Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Урок 32. Пересекаются ли два отрезка?

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель. Напишем еще три новые функции.

Функция LinesCross() будет определять, пересекаются ли два отрезка. В ней взаимное расположение отрезков определяется с помощью векторных произведений. Для вычисления векторных произведений напишем функцию — VektorMulti().

Функция RealLess() будет использоваться для реализации операции сравнения «

Задача1. Два отрезка заданы своими координатами. Составить программу, которая определяет, пересекаются ли эти отрезки, не находя точку пересечения.

Решение
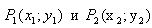
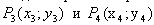
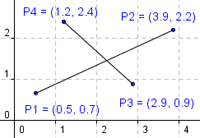
Пусть даны два отрезка. Первый задан точками . Второй задан точками .

Взаимное расположение отрезков можно проверить с помощью векторных произведений:

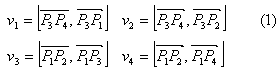
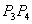
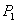
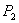
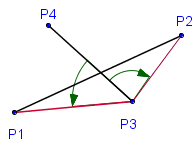
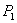
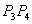
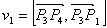
Рассмотрим отрезок и точки и .

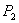
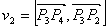
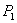
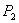
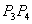
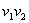
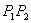
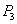
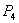
Точка лежит слева от прямой , для нее векторное произведение > 0, так как векторы положительно ориентированы.

Точка расположена справа от прямой, для нее векторное произведение и , лежали по разные стороны от прямой , достаточно, чтобы выполнялось условие и точек и .

Итак, если 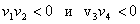, то отрезки пересекаются.

Для проверки этого условия используется функцию LinesCross(), а для вычисления векторных произведений – функция VektorMulti().

Векторное произведение двух векторов вычисляется по формуле:

ax, ay — координаты первого вектора,

bx, by — координаты второго вектора.

Результаты выполнения программы:

Мы написали программу, определяющую, пересекаются ли отрезки, заданные своими координатами.

На следующем уроке мы составим алгоритм, с помощью которого можно будет определить, лежит ли точка внутри треугольника.

Уважаемый читатель. Вы уже познакомились с несколькими уроками из серии «Геометрические алгоритмы». Все ли доступно написано? Я буду Вам очень признательна, если Вы оставите отзыв об этих уроках. Возможно, что-то нужно еще доработать.

Источник

Пересечение отрезков и поворот: определение, свойства, вычисление

Содержание

Аффинное пространство [ править ]

Формальное определение есть, например, на википедии. Неформально: аффинное пространство — удобная геометрическая абстракция, рассматривающая точки (в отличие от векторов линейного пространства). Точки нельзя складывать между собой или умножать на число; к точке можно прибавить вектор, получив другую точку; можно получить вектор разности двух точек. Все приведенные операции обладают геометрически интуитивными и ожидаемыми свойствами.

Наряду с линейными комбинациями векторов рассматривают аффинные комбинации точек аффинного пространства [math]A[/math] : [math]\sum \lambda_i a_i[/math] , где [math]\lambda_i \in \mathbb, a_i \in A[/math] . По определению считают [math]\sum \lambda_i a_i = b + \sum \lambda_i \overrightarrow<(a_i - b)>, b \in A, \sum \lambda_i = 1[/math]

Доказательство: [math]\triangleright[/math] Рассмотрим точку [math]b + \overrightarrow[/math] , тогда [math]\sum \lambda_i a_i = b + \overrightarrow +\sum \lambda_i \overrightarrow <(a_i - (b+l))>= b +\sum \lambda_i \overrightarrow <(a_i - b)>+ \overrightarrow — \sum \lambda_i \overrightarrow = [/math] [math] b +\sum \lambda_i \overrightarrow<(a_i - b)>+ \overrightarrow(1 — \sum \lambda_i) = b +\sum \lambda_i \overrightarrow<(a_i - b)>[/math] [math]\triangleleft[/math]

Также рассматривают понятие аффинной независимости точек (например, три точки на одной прямой аффинно зависимы). Набор [math]\_^[/math] точек называется аффинно (не-)зависимым, если линейно (не-)зависим набор векторов [math]\<\overrightarrow\>_^[/math] .

Ориентация [ править ]

Ориентация векторов [ править ]

Рассмотрим кососимметричную линейную форму от N N-мерных векторов, т.е. функцию [math]f: X \rightarrow \mathbb[/math] , обладающую свойством [math]f(x_1, x_2,\hdots, x_, x_n) = -f(x_n, x_,\hdots, x_2, x_1)[/math] .

Из курса линейной алгебры известно, что любые две такие формы отличаются друг от друга только на некоторый множитель. Зафиксируем одну из таких форм (например, считая, что форма равна 1 на наборе из векторов выделенного базиса). Назовем ориентацией набора из N N-мерных векторов знак значения этой формы на этом наборе векторов.

Отметим свойства ориентации:

• Ориентация линейно зависимого набора векторов равна нулю
• Ориентация меняет знак при перестановке двух векторов в наборе

Неформальное объяснение второго свойства: рассмотрим тройку векторов, таких, что если смотреть из конца первого вектора на второй, то он будет левее, чем третий. Перестановка второго и третьего векторов будет означать, что второй вектор будет виден правее третьего, что означает смену ориентации.

Заметим, что определитель является в точности кососимметричной линейной формой от N N-мерных векторов, а значит, подходит для вычисления ориентации набора векторов.

Ориентация точек [ править ]

Аналогичным образом можно определить ориентацию набора из N+1 N-мерных точек. Ориентацией точек [math]\_^[/math] назовем ориентацию набора векторов [math]\<\overrightarrow\>_^[/math]

Нетрудно заметить, что ориентация набора точек обладает свойствами, похожими на ориентацию векторов:

• Ориентация набора аффинно-зависимых точек равна нулю
• Ориентация меняет знак при перестановке двух точек в наборе

Предикат левый поворот [ править ]

Назовем положительную ориентацию левой, а отрицательную — правой (только соглашение; левая ориентация может не совпадать с интуитивным представлением при выборе кососимметричной формы с другим знаком).

Предикат «левый поворот» по набору точек определяет, верно ли, что их ориентация — левая. Используется в большинстве алгоритмов вычислительной геометрии.

Вычислить ориентацию точек [math]\_^[/math] (и, следовательно, предикат) можно через определитель набора векторов [math]\<\overrightarrow\>_^[/math] .

О точном вычислении ориентации см. раздел Ссылки.

Пересечение отрезков [ править ]

Определить, пересекаются ли два отрезка, можно с помощью предиката поворота. Ясно, что отрезки пересекаются тогда и только тогда, когда для каждого из отрезков его точки не лежат с одной стороны от второго отрезка. Пусть даны отрезки [math]a_0 a_1[/math] и [math]b_0 b_1[/math] . Отрезки пересекаются, если

В случае, если обе ориентации в одной из строк равны нулю, отрезки лежат на одной прямой, и в этом случае пересечение можно проверить способом, аналогичным пересечению отрезков на действительной прямой (считаем, что точки сравниваются лексикографически):

Если предикат вычисления ориентации был абсолютно точным, то таким же будет описанный алгоритм.

Источник

Читайте также:  Что значит фейс хант