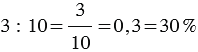Что значит относительно математика

Отношение чисел

Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.

Если вам знакомо понятие отношение чисел, можете смело переходить к теме пропорции.

Что называют отношением двух чисел

Отношение двух чисел — это их частное.

• Отношение 75 к 25 можно записать в виде:
• Отношение 3 к 6 можно записать в виде:

Отношение двух чисел показывает:

• во сколько раз одно число больше другого;
• какую часть одно число составляет от другого.

Покажем на примере, где используется понятие отношение двух чисел.

В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15 . В этом году — 75 . Во сколько раз увеличилось количество участников в этом году по сравнению с предыдущим годом ?

Прежде чем решать задачу, подчёркиваем важные данные. Запишем отношение количества участников в этом году к количеству участников в предыдущем.

При записи отношения двух чисел в знаменатель дроби (вниз) записывается то число, с которым сравнивают.
Обычно это число идёт после слов « по сравнению с … » или предлога « к … ».

Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.

При внимательном изучении правила выше, можно подметить, что правило записанное выше, есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.

Источник

Отношение (математика)

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

Отношение может также означать результат операции деления, например:

Содержание

Формальное определение

n-местным (n-арным) отношением, заданным на множествах , называется подмножество прямого произведения этих множеств.

Иногда понятие отношения определяется только для частного случая для отношения R. Тогда факт принадлежности n-ки этому отношению можно записать как:

.

Арность

• Одноместные отношения соответствуют свойствам или атрибутам.
• Двуместные отношения называют бинарными и обычно записывают инфиксной записью: x R y. Примерами множеств с введёнными на них бинарными отношениями являются графы и частично упорядоченные множества.
• Трёхместные отношения называют тернарными.

Примеры

• Отношение равенства на множестве вещественных чисел — бинарное отношение, обозначаемое символом «=». Ему принадлежат все пары вида , и только они.

• Отношение эквивалентности на произвольном множестве M — бинарное отношение, обычно обозначаемое символом «

  ». Состоит из пар вида , где x и y принадлежат одному классу эквивалентности, и только из них.

• Отношение делимости на множестве натуральных чисел — бинарное отношение, обычно обозначаемое символом « | ». Состоит из пар вида , где x делит y нацело.

Отношения и предикаты

Отношение также может быть задано предикатом на n-й декартовой степени множества M: n-ка принадлежит отношению тогда и только тогда, когда предикат на ней возвращает значение 1 (или «истинно»). Таким образом, можно дать альтернативное определение отношения: если задано отображение , то отношением называется прообраз единицы в . Такое определение бывает полезно в информатике и математической логике.

Предикаты, которые формируются из отношений, заданных в соответствии с основным определением (когда множества в прямом произведении различны), используются в многосортном исчислении предикатов. [1]

Операции с отношениями

Система отношений, сформированная на одном и том же прямом произведении множеств, изоморфна алгебре множеств и допускает применение теоретико-множественных операций и проверок включения одного отношения в другое. Элементами множеств в этом случае являются кортежи элементов (n-ки).

Для отношений, у которых это ограничение не выполняется, теоретико-множественные операции не применимы, но возможны такие операции как соединение и композиция, которые используются в алгебре Кодда, алгебре кортежей и реляционной алгебре.

См. также

Примечания

1. ↑Колмогоров А. Н., Драгалин А. Г. Введение в математическую логику. — М .: Изд-во МГУ, 1982.

Для улучшения этой статьи желательно ? :

• Добавить иллюстрации.
• Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
• Проставив сноски, внести более точные указания на источники.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Отношение (математика)» в других словарях:

Отношение (логика) — У этого термина существуют и другие значения, см. Отношение. Отношение в логике первого порядка двух и более аргументный предикат (многоместный предикат), двух и более предикатное свойство. Знак отношения: R.[уточнить] В терминах отношений… … Википедия

МАТЕМАТИКА — наука, или группа наук, о познаваемых разумом многообразиях и структурах, специально – о математических множествах и величинах; напр., элементарная математика – наука о числовых величинах (арифметика) и величинах пространственных (геометрия) и о… … Философская энциклопедия

ОТНОШЕНИЕ — в логике то, что в отличие от свойства характеризует не отдельный предмет, а пару, тройку и т.д. предметов. Традиционная логика не рассматривала О.; в современной логике О. пропозициональная функция от двух или большего числа переменных. Бинарным … Философская энциклопедия

МАТЕМАТИКА — Между духом и материей посредничает математика. Хуго Штейнхаус Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. Джордж Сантаяна Он стал поэтом для математика у него не хватало фантазии. Давид Гильберт об одном… … Сводная энциклопедия афоризмов

МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера

Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия

Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия

МАТЕМАТИКА — наука о количественных отношениях и пространственных формах действительного мира. В неразрывной связи с запросами техники и естествознания запас количественных отношений и пространственных форм, изучаемых М., непрерывно расширяется, так что это… … Математическая энциклопедия

Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия

Математика майя — Цифры майя Математика майя в своей основе использовала двадцатеричную систему счисления для записи чисел. Вычисления производились на специальном приспособлении (наподобие абака), счётными единицами которых служили какао бобы или различные по… … Википедия

Источник

Математика для блондинок

Математика — это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.

Страницы

среда, 10 августа 2011 г.

Относительность в математике

Все различия между двумя числами или двумя единицами измерения выявляются только при сравнении двух чисел или двух единиц измерения. Все результаты сравнения являются относительными, поскольку зависят от того, какой из двух элементов берется за основу при сравнении. Относительность результатов сравнения отображается различного вида симметриями. Если за основу симметрии берется точка «ноль», то в результате получается зеркальная симметрия. Если за основу симметрии берется точка «единица» — в результате получается обратная симметрия. Для единиц измерения углов обратная симметрия трансформируется в перпендикулярную симметрию, которой обладают значения тригонометрических функций.

Сравнение двух любых чисел не возможно без наличия общего основания, в качестве которого выступает единица измерения. Для расположения любых чисел в порядке возрастания в современной математике в качестве единицы измерения чисел используются системы счисления: двоичная, троичная, восьмеричная, десятичная, шестнадцатеричная и другие. Сравнение двух чисел с различными основаниями не возможно без приведения их к общему основанию.

Сравнение двух чисел при разных единицах измерения становится возможным при использовании третьей единицы измерения – одной из систем счисления, например, десятичной.

Результат сравнения двух чисел описывается понятиями «больше» и «меньше». Относительность сравнения чисел выражается в том, что результат сравнения зависит от того, какое число берется за основу при сравнении. Например, если сравнивать числа 2 и 3, мы получим два результата:

На первом месте принято записывать число, которое берется за основу при сравнении, на втором — то число, с которым оно сравнивается. Результаты сравнения обладают свойством зеркальной симметрии – при изменении основания результат изменяется на противоположный. Точкой зеркальной симметрии является равенство двух сравниваемых чисел. Результаты сравнения двух чисел аналогичны относительной системе координат:

Сравнение двух единиц измерения возможно при наличии общей точки «ноль». Результатом сравнения двух различных единиц измерения может быть заключение о перпендикулярности или параллельности этих единиц измерения. Параллельность или перпендикулярность одной единицы измерения относительно другой – это понятия относительные.

Пояснение для блондинок: Дальше мы посмотрим, как и откуда появилась числовая ось.

Источник

Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу .

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

14 : 7 — отношение числа 14 к числу 7;

6 : 25 — отношение числа 6 к числу 25;

— отношение числа к числу ;

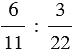
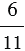
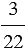
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.

Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

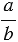
Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Запишем отношение числа 3 к числу 10 и найдем его значение:

То есть отношение двух чисел можно выразить в процентах.

Процентное отношение двух чисел — это их отношение, выраженное в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

Отношение длины прямоугольника к его ширине равно 12 : 100 = .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).

Пусть на карте задан масштаб 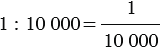, то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

Поделись с друзьями в социальных сетях:

Источник