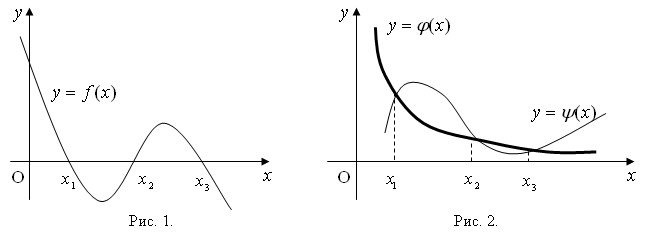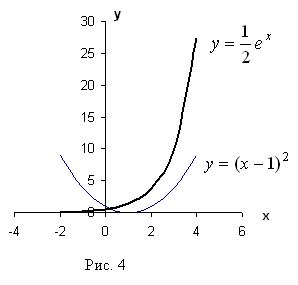- Отделение корней
- Реферат: Отделение корней. Графический и аналитический методы отделения корней
- Содержание
- 1. Отделение корней. 3
- 2. Графический метод. 4
- 3. Аналитический метод (табличный или шаговый). 5
- 4. Метод половинного деления (Дихотомии). 9
- 1. Отделение корней
- 2. Графический метод
- 3. Аналитический метод (табличный или шаговый).
- Что значит отделение корней
Отделение корней
На данном этапе определяются те интервалы области изменения переменной x, в каждом из которых расположен один и только один корень уравнения (3.1). По сути дела на этом этапе определяются грубые приближения значений x с погрешностью, определяемой длиной каждого найденного интервала. Полностью автоматизировать процесс отделения корней, пожалуй, невозможно, так как в нем обязательно присутствует элемент субъективного, интуитивного подхода к решению задачи. Иногда, например, интервал, в котором расположен корень, удается получить из физической сущности решаемой задачи.
При выполнении этого этапа с использованием ЭВМ обычно проводится «табулирование» функции F(x, a1, a2, . ak), т.е. построение таблицы ее значений при различных значениях x, следующих друг за другом с некоторым шагом h:
| x | F(x) |
| x1 | F1 |
| x2 | F2 |
| . . . | . . . |
| xn | Fn |
Например, таблица значений функции x 2 — 12 ln½x½ + 6 sin xна промежутке [1,10] c шагом h = 1 имеет вид:
| x | F(x) |
| 1.0 | 6.05 |
| 2.0 | 0.72 |
| 3.0 | — 3.99 |
| 4.0 | — 6.01 |
| 5.0 | — 1.03 |
| 6.0 | 11.75 |
| 7.0 | 28.42 |
| 8.0 | 43.74 |
| 9.0 | 55.79 |
| 10.0 | 67.72 |
В качестве границ искомых интервалов выбираются такие соседние значения x, в которых соответствующие значения F(x) имеют разные знаки, так как изменение знака функции на некотором интервале означает в силу ее непрерывности, что где-то в пределах этого интервала график функции пересекает ось абсцисс, т.е. уравнение F(x) = 0 имеет корень. В частности, на основании данных из приведенной выше таблицы можно сделать вывод, что уравнение x 2 — 12 ln½x½ + 6 sin x = 0 на промежутке [1,10] имеет по крайней мере два корня: в интервале (2,3) и в интервале (5,6).
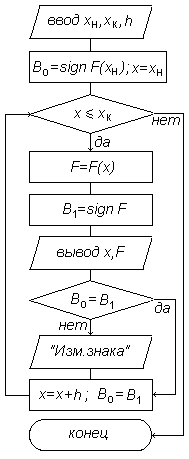 Рис.3.1. Алгоритм отделения корней табулированием функции Рис.3.1. Алгоритм отделения корней табулированием функции |
При выполнении этого этапа нужно проявлять определенную осторожность: во-пеpвых, одинаковые знаки функции F на концах интервала (xi, xi+1) не означают, что на этом интервале нет корней — их может быть, например, два; во-втоpых, при разных знаках на концах интервала здесь может оказаться не один корень, а три или, например, пять.
В приводимой на рис.3.1 схеме алгоритма отделения корней использованы следующие обозначения:
xН, xК — соответственно левая и правая границы промежутка табулирования функции F(x);
x — текущая точка табулирования;
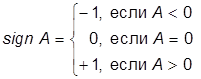
В0, В1 — знаки функции F(x) соответственно в предыдущей и текущей точках табулирования.
В соответствии с данной блок-схемой производится не просто табулирование функции, а, кроме того, анализ знака функции в каждой новой точке и вывод сообщения при его изменении.
Источник
Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
Источник
Что значит отделение корней
1. Приближенное решение нелинейных уравнений
Пусть дано уравнение с одним неизвестным
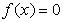
где f ( x ) — заданная алгебраическая или трансцендентная функция.
Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная , логарифмическая, тригонометрические, обратные тригонометрические.
Решить уравнение — значит найти все его корни, то есть те значения х , которые обращают уравнение в тождество, или доказать, что корней нет.
В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью ε . Это означает, что если x — точное значение корня уравнения, а x ’ — его приближенное значение с точностью ε , то | x — x ’ | ≤ ε . Если корень найден с точностью ε , то принято писать x = x ± ε .
Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.
Приближенное решение уравнения состоит из двух этапов:
1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).
2. Уточнение корней до заданной точности.
Отделение корней можно проводить графически и аналитически.
Для того , чтобы графически отделить корни уравнения (1.1), строят график функции y = f ( x ). Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением
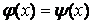
где Φ( x ) и Ψ( x ) — более простые функции, чем f ( x ). Абсциссы точек пересечения графиков функций y = Φ( x ) и y = Ψ( x ) дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).
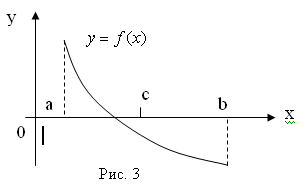
Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке [ a , b ] функция y = f ( x ) принимает на концах отрезка значения разных знаков, т.е. f ( a )· f ( b ) f ( x ) = 0; если при этом производная f ’ ( x ) сохраняет знак внутри отрезка [ a , b ], то корень является единственным.
Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них — метод половинного деления.
Пусть корень отделён и принадлежит отрезку [ a , b ]. Находим середину отрезка [ a , b ] по формуле
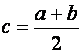
Если f ( c ) = 0, то с — искомый корень. Если f ( c ) ≠ 0, то в качестве нового отрезка изоляции корня [ a 1 , b 1 ] выбираем ту половину [ a , c ] или [ c , b ], на концах которой f ( x ) принимает значения разных знаков. Другими словами, если f ( a ) ∙ f ( c ) a , c ], если f ( a ) ∙ f ( c ) — отрезку [ c , b ]. Полученный отрезок снова делим пополам, находим c1 ,
вычисляем f ( c 1 ), выбираем отрезок [ a 2 , b 2 ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие
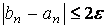
то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять
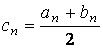
Пример . Пусть требуется решить уравнение
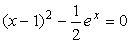
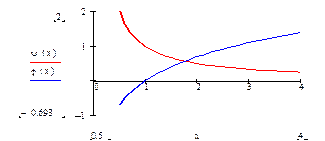
с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду
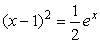
и построим графики функций (рис. 4):
Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].
Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:
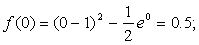
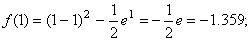
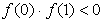
Уточнение корня выполним методом половинного деления.
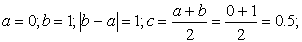
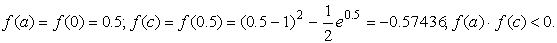
Корень принадлежит отрезку 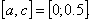
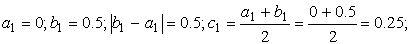
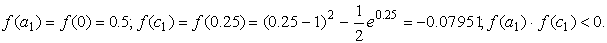
Корень принадлежит отрезку 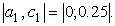
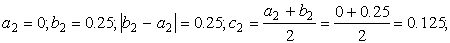
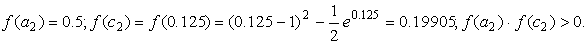
Корень принадлежит отрезку 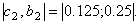
Источник
 Министерство образования и науки РФ
Министерство образования и науки РФ 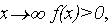 при
при 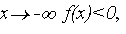 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.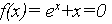 видим, что
видим, что 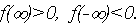 Обнаружив, что
Обнаружив, что 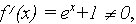 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).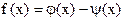 и строить графики функций
и строить графики функций 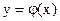 и
и 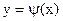 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.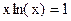 .
.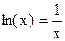 , т.е.
, т.е. 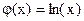 и
и 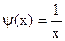 .
.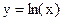 и
и 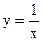 .
.