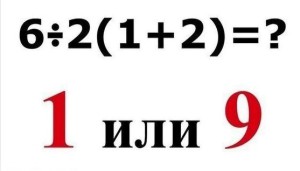Решение вирусных школьных задач
Две однотипные задачи, которые в разное время взбудоражили интернет. Сталкиваются титанические плиты мнений, летят волосы, брызжет слюна, ломаются карандаши и ручки, рушатся семьи… Последнее не точно, но всё может быть.
Проблема вирусных школьных задач
Я рассмотрю здесь последнюю нашумевшую вирусную задачу, а именно:
Алгоритм чтения математических выражений такой:
- в первую очередь мы определяем порядок действий;
- после этого читаем и выполняем их, начиная с последнего.
Но тут появляется первый камень преткновения – это отсутствие знака умножения между числом 2 и открывающейся скобкой. Этот камень успешно преодолевают все: и те, кто из школьной математики помнят только, что знак умножения можно опускать, и те, которые знают, в каких случаях допускается пропуск знака умножения, а именно, пункт 3.
Правило опускания знака умножения в выражениях.
Знак умножения при записи математических выражений можно опустить в таких случаях:
1. между буквенными множителями;
2. между числовым и буквенным множителем;
3. между множителем и скобкой;
4. между выражениями в скобках.
То есть, нашу задачу мы можем записать так:
Вторым камнем преткновения является определение порядка действия . Здесь царит настоящая чехарда! Одни представляют это выражение в виде произведения дроби \(\frac<8><2>\) и суммы \(2+2\) , что в итоге приводит их к результату 16 . Другие, вспоминая школьное правило порядка действий, сперва находят сумму, заключенную в скобки, а потом выполняют действия одинаковой ступени (умножение и деление).
Вторые также делятся на два лагеря: на тех, которые помнят со школьной скамьи, что действия одной ступени выполняются по порядку слева направо, и получают \(8\div 2=4\) , \(4\times 4=16\) , и тех, которые утверждают, что действие умножения имеет приоритет над действием деления, поэтому \(8\div 8=1\) .
Кто же из них прав?
Решение вирусных школьных математических задач с опущенным знаком умножения
Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.
Первым действием , с чем никто не спорит, находится выражение в скобках. Получаем:
1) \(2+2=4\).
А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения .
Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.
Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается между множителем и скобкой . А если есть явное указание на существование одного из множителей , значит существует , как минимум, ещё один множитель , а именно: выражение в скобках.
Предположим , что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2 , потом умножение 4 на 4 . Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем 2 и скобкой ( 2 + 2 ), что является нарушением правил опускания знака умножения, и такая трактовка условия некорректная . Для корректного представления частного \(8\div 2\) , оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\).
Следовательно, мы можем рассматривать 2 перед скобкой только как множитель , 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\) . Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.
Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:
\(8\div [2 \times (2+2)]\) .
Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.
А найти результат деления числа на произведение можно двумя способами:
1) делимое число разделить на результат произведения;
2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.д.
Поэтому, второе действие решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:
2) \(2\times 4=8\).
Остается только выполнить третье действие – найти частное от деления 8 на 8 :
3) \(8\div 8=1\).
Итак, результат решения задачи:
\(8\div 2\times (2+2)=1\).
Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений : при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:
\(a\div ( k\times l\times m)=a\div (klm)=a\div klm\).
А в нашем случае мы имеем результат этой записи , то есть, в делителе , который выражен произведением с опущенным знаком умножения, были опущены скобки . И нам следует выполнить обратные действия , то есть: восстановить опущенные скобки и знак умножения . Тогда наш изначальный пример приобретет такой вид, тождественный начальному:
\(8\div [2\times (2+2)]\).
Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.
Проверка решения вирусных математических задач с опущенным знаком умножения
Получив результат выполнения действий, его нужно проверить .
Проверкой данной вирусной математической задачи с опущенным знаком умножения, а также еще одним способом ее решения, служат тождественные преобразования исходного выражения .
Итак, мы имеем выражение \(8\div 2(2+2)\) . Можем ли мы его упростить, просто заменив выражение в скобках его суммой ? Ответ: нет . Потому что в этом случае у нас получается опущен знак умножения между двумя числами , что противоречит правилу , рассмотренному выше.
Упростить выражение, не нарушив правило опущения знака умножения, мы можем, представив выражение в скобке в виде буквы :
пусть \(x=(2+2)\),
тогда выражение приобретает вид:
\(8\div 2x\),
что не противоречит правилу опущения знака умножения. Идем далее:
\(8\div 2x=4\div x=4\div (2+2)= 4\div 4=1\).
Как видите, проверка показала правильность решения этой вирусной математической задачи.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.9 / 5. Количество оценок: 92
Источник
Блог инженера
Инженерный блог
Вот сижу что-то ночью опять… Решил написать своё мнение о популярном сейчас вопросе: один или девять?
Я думаю, по изображению сверху стало уже понятно, о чём идёт речь. Знак умножения – он опущен перед скобками, и… как считать?
Посмотрим с двух позиций.
1) Знак умножения просто опущен. Тогда изначальная запись выражения выглядит так: 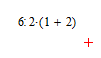
Шесть делим на два, умножаем на сумму единицы и двойки и (всё просто супер, детка) получаем девять. Ответ – 9. Вроде всё красиво, но…
2) Знак умножения не просто опущен. Как так – не просто? А просто так и нельзя опустить. Итак, вот есть инфа, которую, похоже, взяли из учебника за седьмой класс (изначальный источник не найден, но нагуглил в методичке какого-то математического лицея):
Что это для нас значит? А то, что если знак умножения опустили так, как описано в предыдущем пункте, то поступили неправильно, потому что двойка в примере – не множитель перед скобкой, а просто один из трёх множителей (если рассматривать деление как частный случай умножения). Поэтому, если он опущен правильно, то имеем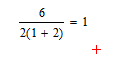
И это в том случае, если правило выше абсолютно точное. Но без конкретного источника (утверждается, что это школьный учебник) можно не рассчитывать на то, что оно точное. В школьной математике много требований, которыми даже в разделах вышки порой пренебрегают.
Это правило, к тому же, может оказаться неполным: вдруг нельзя опускать знак между скобкой и множителем в такой ситуации? Составлял бы я правила, я бы так и поступил. Спорная ситуация? Ставь ещё одну пару скобок! Будет вполне однозначно и всем понятно.
От себя скажу, что я часть после деления воспринимаю как нечто целое, т.е. скобку с множителем, мне это кажется вполне естественным. Почему же возникает спор? Многие запоминают, что «всегда можно опустить знак умножения». Но это не так. 2 умножить на 3 не есть 23, а произведение переменных c, o и s не всегда будет правильно понято.
На первый взгляд становится понятно, что человек, сказавший, что ответ – 1, просто забыл о порядке действий, его смутило отсутствие знака умножения. Здесь это чем-то напоминает мне загадку о ножках в комнате (где вопрос о том, сколько ног у животных в комнате. Вскользь упоминается, что ещё стоит и кровать. Если человек забыл про ножки кровати, он лох, если посчитал их, то тоже лох, ибо это не ноги, а ножки. Если посчитал ноги животных, то тоже лох, ибо у них лапы. Короче, вне зависимости от ответа человек – лох и ставит жирафа на аватар). А так как его действия (которые сначала нам показались такими) неправильные, то наше образование – говно и всё такое. Но если копнуть глубже, то действительно встаёт вопрос – а сколько? Если в реальной жизни в важном месте встретить такое, то, независимо от правильного ответа, нужно серьёзно поговорить с человеком, который написал это выражение и не уточнил, что он имел в виду.
Да, помню в какой-то методичке по экономике (у нас слабо вёлся этот предмет, и методички слабые были) была буквенная формула с такой же проблемой. Знак деления, справа большое достаточно выражение. Я тогда засомневался, в итоге нашёл правильную формулу. Да, там после деления всё должно было быть знаменателем. Но там это было однозначно неверно. Люди, пишите не правильно, а понятно 🙂
6/2(1+2) : 143 комментария
Однозначно 9.
Действия деления и умножения имеют одинаковый приоритет, дробной черты, отделяющей знаменатель от числителя, нет, дополнительных скобок нет, значит порядок: сложение, деление, умножение.
Но если воспринимать действие после деления , как целую часть, то ответ будет =1.
Вообще-то со времён школы выполняются сначала действия в скобках, затем умножения и деления слева направо поочерёдно, затем сложения и вычитания слева направо поочерёдно. пропущен знак умножения или нет — неважно, важно, что он понятен и присутствует. Деление (двоеточие) не то же самое, что дробная черта. Данное выражение можно было написать и как 6:2х3.
Сам пост читаем
Сам пост читаем: между одним из множителей и скобкой.
=Умножение.
В случае умножения — то есть знак умножения просто опущен. Значит 9. Что в вашем посту, кроме не очень понятных выводов после приведенных вами же аргументов, говорит за 1?
Всё просто. Надо сделать проверку. Посчитать обратно. Только представим (1+2) как неизвестное. Пусть будет х.
Итак.
Если 6:2х=9
То 6=2х × 9
18х = 6
х = 6/18 = 1/3
Не подходит.
А если 6:2х=1
2х = 6
х = 3
Подходит (1+2) = 3
Значит правильный ответ основной задачи 1
Данное выражение можно записать и так…
2 — это общий множитель…
6/ (2*1 + 2*2) ….
без скобок — не будет общего множителя
6/ 2*1 + 2*2, поэтому результат будет 1, а не 9
Тогда, 6/2*1=3, далее 3+2*2=7…..
.
Так записать нельзя.
Потому, что действие в скобках имеет главный приоритет.
Это если арифметика. А если алгебра? Там свои законы и правила расчётов, и тогда правильный ответ будет 1.
На всю математику одни законы без вариантов.
как целую часть можно воспринимать если множитель 2 мы до этого вынесли из скобок как общий множитель. 6:(2+4). Но если мы выносим общий множитель за скобки то получается 6/2(1+2)=1 или если без дроби то 6:(2(1+2))=1. но в данном примере 6:2(1+2) ответ только 9
А как вообще появилась эта двойка за скобками ? Это общий множитель для 1 и 2 . Изначально было это было
2 и 4 и выглядело всё так
6 : ( 2 + 4 )=1
Взяли и вынесли общий множитель за скобки
6 : 2 (1+2) = 1
И что , от этого должен поменяться результат ?
2(1+2) это не просто скобки это блок и решать это надо блоково . Сначало надо вернуть этот множитель опять в скобки и только потом складывать .
Согласитесь , что эти 2и 4 взяли в скобки для того что бы начать действие со скобок . . При ответе 9 НЕ ИМЕЕТ ЗНАЧЕНИЕ НАЧНЁТЕ ВЫ СО СКОБОК ИЛИ ИМИ ЗАКОНЧИТЕ . Ответ будет одинаков и так и так . Получается скобки здесь совершено не нужны , их роль нулевая . И совсем другая картина при блоковом решении и ответе 1 . Этот факт есть косвеное доказательство — ответ 1 логичен . Если вы не начнёте решение с открытия скобок ответ будет другой . Введение в пример скобок обьяснимо и логично , при ответе 9 правило ,, начинать надо со скобок ,, не имеет смысла
Вот в том-то и дело, что блок один. А в случае 6:2(1+2) вы блок (2+4) превратили в два. 6, 2 и (1+2). Изначально же было всего два блока 6 и (2+4). По правилам это будет так 6: на блок (2+4). Соответственно, если вы хотите изменить что-то в блоке, то и заключайте этот блок в отдельные скобки: 6:( 2(1+2) ). Соответственно и результат не изменится.
Если при ответе 9 скобки не имеют смысла, тогда мы считаем просто слева направо, и получаем в итоге 5. Это математика. Тут нужны цифры , а не логика. Сначала скобки, потом всё слева направо.
«При ответе 9 НЕ ИМЕЕТ ЗНАЧЕНИЕ НАЧНЁТЕ ВЫ СО СКОБОК ИЛИ ИМИ ЗАКОНЧИТЕ .» — немного не верные мысли … это в данном примере так совпало, что 6/2 будет равняться тому что в скобках, т.е. 2+1, а если взять вот такой пример:
Если уж преобразует единое выражение, то и показывайте, что это единое выражение, заключая его в скобки, а не записывая, как левая пятка захотела
А как это вы так лихо вынесли двойку и записали 6 : ( 2 + 4 )=1 в виде 6 : 2 (1+2) = 1 ?? Что за бред??
Если уж выносите, то и пишите правильно: 6 : ( 2 + 4 )=1 тождественно 6 🙁 2 (1+2)) = 1.
А 6 : 2 (1+2) = ДЕВЯТЬ!
В качестве примера, где скрытое умножение обладает повышенным приоритетом по отношению к обычным умножению и делению можно считать «Курс теоретической физики» Ландау-Лифшица и другую физическую литературу.
Уточните на каких страницах «Теоретики» виден этот приоритет? (люблю проверять подобные факты в первоисточниках).
Т.е. статью вы не прочитали)) И математику в вузе не изучали. Учебники для 3го класса пишут люди с высшим математическим образованием. А эта задачка написана дурачками.
Тимофей, загляните в учебник 5 класса и там вам расскажут, что знак деления в виде двух точек АБСОЛЮТНО эквивалентен дробной черте.
Впрочем, весь цимус даже не этом.
Здесь работает другое правило — Распределительный закон умножения
k(m+n)=km+kn
А порядок действий, в общем виде, ЗВУЧИТ так:
Число деленное на произведение суммы.
Пусть это звучит глупо, я всегда (с тех пор как узнал об алгебре) рассматривал запись без знака умножения как «более тесную» связь между числами. Т.е. если a=3, то 6÷2a=6÷(2×a)=1, а не 6÷2×a=9. К сожалению, я не помню, было ли это взято из учебника или придумано мной, но умножение переменной на её коэффициент в алгебре должно выполняться раньше любых других операций, потому что это (простите за бурную отсебятину, пишу как понимаю) приведение чисел из алгебраического в арифметический вид. В случае со скобками я точно также воспринимаю число перед опущенным знаком умножения как коэффициент перед переменной.
Именно! Я тоже так считаю)
все так считают. Потому что умножение перед скобками считается первым (оно обычно не указывается и считается первым. Как будто там еще одни скобки стоят)
Правильный ответ 1
В том то и дело, что скобки еще одни не стоят!
Если мы берем пример 2:2(3-1), то в случае, когда 2(3-1) были бы знаменателем оно записывалось бы как 2:(2(3-1)), это неотъемлемая часть правила написания алгебраического выражения.
Вы не чего не забыли 2:2(3-1)=2:(2*(3-1)≠2:2*(3-1)
Всё правильно, правильный ответ 1
а — неизвестное, не сравнивай.
У тебя ОЧЕНЬ бурная отсебятина 🙂
Правильный ответ 1
Перед скобками знак умножения просто не пишется но имеется ввиду что он есть
В случае с 2а все равно подразумевается знак умножения, и все равно действия идут слева направо. Проверьте себя любыми школьными примерами и поймёте. 😉
Тогда решите пример 655, 3) из Сборника задач по алгебре для 6-7 классов, П.А. Ларичева.
Ссылку прилагаю, ответ в задачнике есть.
https://russianclassicalschool.ru/biblio/13_sr_sk_uceb_algebra.pdf
Милый мой где же Вы в данном выражении 6:2(1+2) нашли a, x, b или хотя-бы с что бы иметь право ссылаться на литературу 1952 года выпуска где к тому же не дано объяснение решения?
А Вы, ненаглядный мой, примеры 6:2(1+2) и 6:2(а+2) будете решать по-разному?
Вы совершенно правы!Благодаря Вашему объяснению я нашла подтверждение своей уверенности в правоте своего мнения.
Так и есть. Выражение 6:2а читается, как «6 делим на 2а».
Да дело то совсем не в более тесной связи, а распределительном законе умножения — a(b+c)=ab+ac.
Из которого следует, что множитель лишь визуально вынесен за скобку, в РЕАЛЬНОСТИ же относится именно к тому, что находится внутри скобок.
Пост, конечно, старый, но я все же про комментирую. Вот у автора серенькая плашечка, так называемая выдержка из учебника, со случаями возможного пропуска знака умножения, и там третий пункт должен развеять все сомнения: это как раз наш пример, когда знак умножения пропущен между множителем и скобкой. Не знаю, как в школах учат сейчас, но в далеком 98-м году, когда я училась в седьмом классе речи о приоритетности правой части уравнения над левой рассматривалось только в случае ограничивания этой самой части скобками. И только в этом случае.
Нет никаких «но» и «вдруг»: в данном конкретном примере пропуск знака умножения допустим, и выражение необходимо читать, как 2*(1+2).
Я знаю, что вас смущает. Можно сравнить это с визуальной иллюзией, ведь внешне и без знака умножения часть 2(1+2), «на глаз» так сказать, воспринимается действительно, как единое целое, которое психологически хочется увести в знаменатель полностью.
что мы имеем в итоге, считая последовательно слева направо с учетом отдельно вычисляющейся суммы в скобках: 1-й множитель 6/2 (шесть вторых) и 2-й множитель (1+2) . Ну и считаем их произведение. Получаем 9. А методичку сожгите.)
Ваша учительница по математике перевернуламь в гробу.
Ваша учительница по русскому языку сделала то же самое.
Для единицы исходник должен выглядеть так:
6:(2(1+2))
Исходный материал был 6 : ( 2 +4 ) =:
Из (2+4) вынесли общий множитель 2 за скобку …. и что , от этого он стал ,, жить самостоятельной жизнью ,, ?
НЕТ.
Ну если вы, конечно, не отменили Распределительный закон умножения!
Лучше прочитайте правила раскрытия скобок « a(b+c) =ab+ac
Это конечно все хорошо…но как тогда решать простейшее выражение. 8:2( а+с). На протяжении 6 лет, нас учили раскрыть скобки: 8:2а+2с! И в этом случаи результаты будут иметь разные значения… интересно было бы узнать мнение профа!)))
ничего подобного, максимум что может быть это 8:(2а+2с), поэтому удобнее и правильнее было бы записать данный пример, как 4(а+с).
8:2( а+с) = 8:2а+8:2с
я просто в ахуе.. куда катится мир
в примере 8:2(а+с) будет ответ 4а+4с, никак не может один делитель делить 8, а второй стоять отдельно в сумме.
8:2(а+с)=4(а+с)=4а+4с
Такой ответ будет, если мы хотим получить Четверку. А если хотим Пятерку (отлично), то ответ 4(а+с)
В вашем случае скобки раскрываются так: 8:2а + 8:2с
блин, вы чо все с дуба рухнули? Если у вас так туго с арифметикой запустите excel или калькулятор виндовый, перевидите в инженерный, там есть скобки и посчитайте. Уж в мелкософте не довны работают, они то в отличие от вас точно знают как правильно это по считать. ответ 9 если чо.
В том то и дело, что калькуляторы дают разные ответы
Мой CITIZEN SRP-285N (22Eur — самый дорогой что был в магазине) решает так:
6/2(2+1)=1
6/2*(2+1)=9
Вот и спорь теперь с ним 😀
NB! Кст, попробуй Windows’кий калькулятор. Там вообще свою тему прёт, если * не ставить 😀
я пробовал считать в эксэле результат такой:
когда я набрал в ячейке =6/2(1+2)
он мне написал что там не хватает умножения.
«Приложение Microsoft Excel обнаружило ошибки во введенной формуле. Принять предполагаемые исправления?
=6/2*(1+2)»
То есть он САМ исправляет. САМ ставит там знак умножения. И тогда результат будет 9. Без знака умножения не считает.
А если ещё скобки раскрыть или же двойку в скобки внести, ни кто не думал, что это мать ее, математика, наука черт знает о чем, абстракция, можно доказать что угодно
Если, что-то смущает, то надо видоизменить написание примера 6/2(2+1)=6/(2+1)2=1, потому что от перемены мест слагаемых и произведения результат не меняется, а вот деление другое дело и дробь и деление это одно и тоже. Всё, что стоит за знаком деления идет в знаменатель… так, что 6/6=1. А 9 получилось бы, если бы было написано так: (6/2)(2+1)=9 — и это уже произведение дроби и суммы. Решайте как написано, не надо придумывать….
Это математика, люди! А не психология…. здесь нет задач: типа автор думал, и кто во что горазд и т.д….. если записано так, значит и ответ такой, если написано иначе значит и ответ был бы другой.. А притягивать за уши, и логически рассуждать это чистой воды мошенничество и рассчитано на людей безграмотных…. В школе я училась давно, но видно хорошо меня учили….))))
Всем успехов!
>Всё, что стоит за знаком деления идет в знаменатель…
>потому что от перемены мест слагаемых и произведения результат не меняется
Да, но деление стоит слева и у него приоритет, так что если хотите менять члены произведения местами, то будет так:
Ебанулись? Если бы было написано так 6/(2(2+1) то за деление ушло в знаменатель, а как в примере в знаменатель уйдет только 2
О боги, вы сейчас 1/2 превратили в 2, а 2+1 превратили в 1/(2+1). Вы серьезно. Иногда мне кажется, что люди на полном серьёзе пишут такие вещи, чтобы победить кого-то…. Чтобы сидел где-то аноним и думал: какие же вы тупыыыые. И фейспалмил с этого, а гнев выразить не на кого, потому что все в интернете…
. Энгри смайлы.
Ага, как же, идёт всё в одну кучу. Обратитесь к математике и программированию. Чтобы после деления всё относилось к делителю — необходимо чтобы оно находилось в скобках. Ну и неприменимая теория про перестановку морганиях полный абсурд, давайте ещё 6 поменяем с 2, почему бы и нет
Есть разница между умножением со знаком и без знака. А разница состоит в том, что при умножении без знака произведение рассматривается как цельная величина. На бытовом примере: если 2а это литр жидкости, то 2×а это два пол-литра жидкости.
Рассмотрим пример:
2а:2а=1
при а=1+2
2(1+2):2(1+2)=6:2(1+2)=6:6=1
Для тех, кто не помнит этого правила, предлагаю решить пример на понимание. Для этого необходимо решить пример №797 из «Сборника задач по алгебре», Часть I, для 6-7 классов. (П.А. Ларичев) и сверить полученный результат с ответом. Сборник можно скачать в интернете бесплатно.
Нет сомнения, что те, кто сможет решить пример из Сборника, однозначно дадут правильный ответ на спорный пример:
6:2(1+2) = 1
Послушайте. Число перед скобками определяет количество того, что в скобках. Объясню. У нас шестьдесят литров допустим пива. В скобках — одинарная порция. Выражение 60 : (5-2) = 20 значит, что одинарная порция составляет (5-2) = 3 литра. И хватит по одинарной порции на 20 бухариков. А выражение 60 : 2(5-2) = 10 значит, что по двойной порции хватит уже только 10 бухарикам. Т.к. выражение 2(5-2) — это уже двойная порция. Это то же, что и 60 : 2х. Когда опущен знак (умножить), то скобки теряют смысл. Это значит писать 60 : (2х). Короче, выражение 60 : 2(5-2) равно выражению 60 : (2*(5-2)). Когда в данном случае пользователь пытается восстановить специально опущенный знак «умножить» между множителем и скобкой, то следует восстановить и специально опущенные в таком случае скобки. Такова грамота писания математических выражений. И знак «умножить» и скобки опущены в данном случае прямо согласно грамоте писания математических выражений. Вот и все.
Правила раскрытия скобок, основаны на распределительном законе умножения:
a(b+c) = ab + acНа самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)3 × (4 + 5) = 3 × 4 + 3 × 5
Отсюда следует: 2(2+1) =2*2+2*1=6, 6:6=1
Но эта задача не для 4 класса, что и сбивает с толку
Ну конечно, только почему же, раскрывая скобки, вы куда-то дели шестерку?
6/2(1+2) = 6/2*1+6/2*2= 3+6=9
Говорили , нужен пруфф , который можно проверить . Вот https://resheba.ws/urok/matematika/05/001/067.html Скобки и действия с ними в приоритете, потом все остальное. Ответ 1.
В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c).
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
https://russianclassicalschool.ru/biblioteka/matematika.html
Поскольку в спорном примере знак умножения опущен, то спорный пример алгебраический.
Исходя из вышесказанного: 6:2(1+2) = 1
Но заявленная выше задача чисто арифметическая, почему вы в выражение без переменных пытаетесь буквы добавить?
Задача чисто алгебраическая, поскольку пропуск знака умножения — правило алгебраическое. «Алгебраическое выражение может не содержать чисел, обозначенных буквами».
Что же Вы не полностью процитировали абзац у товарища Шустефа М.В.?
Позволю продолжить:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20*2=80:40=2 вместо обычного: 80:20*2=4Х2=8. Однако это предложение не нашло поддержки.»
Т.е. если уж и аппелировать к работе Шустефа М. Ф., то очевидно, что:
а) товарищ Гончаров указывает — пишите сразу понятно (тут все согласятся, т.к. вопрос оказался интересным);
б) если африфметика противопоставляется алгебре, то в нашем случае как раз имеет место «пример П. С. Александрова и А. Н. Колмогорова», и из того, как он подан у Шустефа М. Ф. понятно, что «обычно» пример с цифрами решается слева на право, а не отдавая приоритет умножению.
Поэтому так себе аргумент на самом деле.
Пропуск знака умножения это алгебраическое правило. Буквенное обозначение – не единственный признак алгебры. Поэтому спорный пример алгебраический и пропущенный знак умножения связывает компоненты сильнее, чем деление. Поэтому 6:2(1+2) = 1.
Что же касается предложения П. С. Александрова и А. Н. Колмогорова, которое не нашло поддержки, то поэтому, в случае если знак прописан, мы имеем: 6:2×(1+2)=9.
Прочитайте вслух выражение 8:2а
Каждый читает так, как решает. Я прочитаю вслух: “8 разделить на 2а”. А мой оппонент, который предлагал такой же метод, читал: “число 8 разделить на 2 и умножить на а”.
Вот давай теперь в твой пример подставим:
a = 2
b =2
c = 2
получаем:
2:2*2=2:(2*2) что в итоге 2:2*2 = 2:(4) и это по твоему правильно?
Чтобы получить 1 в исходном примере должна быть запись:
6:(2*(2+1)) и только так. Даже через переменные:
6:2(a+b) = 6:(1/2а + 1\2b)
Перемещая делитель внутрь скобок не забывайте делить то что внутри скобок на него а не умножать!
2:2*2=2:(2*2) Не верно поставлено равенство. Если знак умножения прописан, то 2:2*2 = 1×2 = 2.
2:(2*2) = 2:4 = 0,5.
Поскольку опущенный знак умножения связывает компоненты сильнее, чем деление, то в случае написания знака умножения мы имеем:
6:2(1+2) = 6:(2×(1+2)) = 6:(2×3) = 6:6 = 1.
Методика преподавания алгебры в восьмилетней школе, Репьев В. В., стр. 81
Дебил, а не инженер
Сами же написали:
Случаи возможного пропуска знака умножения:
1) между буквенными множителями;
2) между числовым и буквенным множителем;
3) между множителем и скобкой;
4) между выражениями в скобках.
1) сразу пропускаем, так как буквенного множителя нет
2) тоже самое
3) То есть между множителем и скобкой, то есть множитель в данной ситуации 6:2, но никак 2 не может рассматриваться как отдельное число, только если бы вместо деления был бы знак минус.
4) между выражениями в скобках, сомнительно, но тоже можно применить (6:2), так как в данном выражении 2 не выступает как что-то отдельное и всю часть примера после знака деления нельзя рассматривать как знаменатель.
«в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления» ну это для меня что-то новенькое…
Для тех, кто прогуливал уроки математики, а на уроках ворон за окном считал это “что-то новенькое…”
Вы неверно раскрыли скобки, так не раскрывают 6:(2×1+2×2)=1Общий множитель можно внести в скобку
А давайте ещё делимое внесём в скобку. (6:2×1+6:2×2)=9
%)
Есть простой пример 6/2(1+2) = 1 или по другому 6/х = 1 В результате х = 6
(во всех примерах 6 в числителе, а 2(1+2) в знаменателе)
Те, кто видит в ответе 9 пусть решат пример 6/х = 9. В результате х = 2/3.
Отлично, значит они считают, что 2(1+2) = 2/3. Пусть докажут это!
Для тех, кто реально работает с формулами 6/2(1+2) = 1
Для жертв ЕГ это 9. Не дай бог им доверить расчет дома, рухнет.
Такой пример решают в начальной школе. Простой способ, представить числа в скобках как «а».
Получаем: 6/2а= 3а
а= 2+1
3а=3*(2+1)=3*3=9
Каким образом Вы превратили 1/2 * (1+2)=3/2 в = 1/6 ?
Не дай бог, что бы у делимого отнимали делитель и засовывали его под икс другому множителю. Вот и доказывай потом таким
Для не жертвы ЕГ(Э!) сложно понять, что разные ответы основаны на том, что запись нельзя трактовать однозначно? Даже в примерах выше приведены выдержки из учебника, в которых сами математики до конца не уверены в корректности. Кроме того те кто будет вести «расчет дома» — явно будут знать какой порядок действий должен быть, так как при необходимости они сами будут эту запись составлять.
>>значит они считают, что 2(1+2) = 2/3. Пусть докажут это!
Ничего, что такое равенство получилось сугубо из твоего личного видения ситуации, а конкретно из примера 6/(2*(1+2))? Когда те, кто придерживаются ответа 9, эту запись рассматривают так 6/2*(1+2) ? Или ты предлагаешь бред придуманный тобой доказать?
В вашем примере уравнение должно быть записано так:
(6/х)*(2+1)=1
Отсюда х будет равен 18. А это не так.
Если же решить уравнение (6/х)*(2+1)=9
то х=2 . Что и требовалось доказать.
Для жертв ЕГЭ и для тебя в частности предлагаю воспользоваться гуглом, или учебником по математике для младших классов, где прочитать параграф о порядке арифметических действий )))
Сначала раскрываем скобки, а потом выполняем слева направо все действия умножения и деления.
6/2(1+2) = 6:2*3 = 3*3 = 9
Чувак выше пробил дно. Доказать что 1/2*(1+2)=2/3? Сразу видно опытного хумунитария. Или троля который просто выдирает кусок из контекста. Если нужно выражение представить в виде делители без употребления черты то его берут в скобки. Нет скобки — приоритет в порядке очереди.
А кто вам дал право 2(2+1) пихать в знаменатель?
Вот от ваших расчетов дома и рушатся!
Тем кто считает что множитель 2 для (2+1) и 2(2+1) знаменатель (делитель) еще немного арифметических правил:
«…
Знак умножения в некоторых случаях можно опускать, а в некоторых — нельзя:
когда знак умножения принято опускать:
перед скобками:
5·(3+C) = 5(3+C)
перед буквами в буквенном выражении:
5·A·B = 5AB
знак умножения всегда ставят перед числом:
5A = A·5
Свойства умножения:
Переместительное свойство — от перестановки местами множителей произведение не изменяется:
А·B = В·А
…»
А теперь смотрим:
6:2(2+1)=6:(2+1)*2 (обана! умножение вернулось) = 6:3*2 =4
еще один ответ в копилку. 🙂 Те кто получает ответ 1 нарушает Переместительное свойство умножения! и в выражении у нас знак деления, а не дробная черта разные вещи по сути, знак деления можно заменить дробной чертой но только правильно!
А если множитель 6:2 (а почему нет?), то все правила соблюдаются!
6:2(2+1)=(6:2)(2+1) (разве мы не имеем права ставить скобки не нарушая правил? Возьмем множитель в скобки! Причем знака умножения до сих пор нет) = (6:2)*3 (помним что перед числом всегда знак умножения) = 3*3=9
и мы не нарушаем Переместительного свойства: (6:2)(2+1)=(2+1)(6:2)=3*3=9
Все еще считаем 2 множителем для (2+1) и 2(2+1) знаменателем?
“немного арифметических правил”
Пропуск знака умножения – правило алгебраическое. Поэтому забудьте арифметику.
“когда знак умножения принято опускать: перед скобками: 5•(3+C) = 5(3+C)”
Не перед скобками, а между МНОЖИТЕЛЕМ и скобкой. Двойка МНОЖИТЕЛЬ по отношению к скобке и при любой конфигурации математического выражения, множитель 2 должен быть умножен на скобку.
Множитель не 2, а 6/2. Какого хрена вы разрываете выражение в удобном вам месте? И вообще, как вы решите, например, такое 6/2(1+2)(2+3) ?
Согласен, напоминает 2(1+2) как будто (1+2)(1+2) то есть 6÷3×3 что ли. Так здесь и третий вариант ответа 🙂
2(1+2)=(1+2)+(1+2)=6 , 6÷6=1, а Вы неправильно решили 2(1+2)не=(1+2)(1+2)=(1+2)^2=3^2=9
Веселюсь уже второй день! как-то раньше не натыкалась на этот прикол. самое удивительное, что все так близко к сердцу приняли этот софизм. вот интересно, откуда у него ноги растут? кто-то же «нарисовал» такое чудо?
друзья! эту «проблему» не решить в отрыве от контекста. каков источник возникновения данного выражения?
если это арифметическое выражение (ну там, например, по задаче), то оно ЗАПИСАНО НЕВЕРНО. так как при выполнении АРИФМЕТИЧЕСКИХ операций необходимо записывать ЗНАКИ действий. и если «восстановить» знак умножения, то это 9 (к счастью предложения Александрова и Колмогорова не встретили поддержки). то есть уточняю: при выполнении арифметических операций с числами у умножения нет преимуществ перед делением.
а вот если рассматривать это прикольное выражение само по себе, как есть, то отсутствие знака умножения говорит о том, что мы имеем дело не с числами, а с одночленами (если что, то число является частным случаем одночлена). и тогда действительно, двойка относится к сумме. и делить 6 надо на результат умножения, то есть ответ 1.
преклоняюсь перед автором этого софизма. такой хайп запустил!
Прочитайте вслух выражение 8:2а
(Это для тех, кто не понял)
Восемь делить на два и умножить на а. Прочитал, что дальше?
А не легче просто проверить таким способом.
a/2(1+2)=6
a/6=6
a=6*6
a=36 что даёт нам не правильный ответ
А если :
a/2(1+2)=1
a/6=1
a=1*6
a=6 а так вдруг все сошлось)
Вообще задача стояла так ,6÷2(1+3) не пойму что вы обсуждаете,
Знак деления — математический символ в виде двоеточия (:), обелюса (÷) или косой черты (/), используемый для обозначения оператора деления.
Основная функция скобок – менять порядок действий при вычислениях значений числовых выражений. Например, в числовом( арифметическом )
выражении это
5*3+7 сначала будет вычисляться умножение, а потом сложение:
5⋅3+7=15+7=22
А вот в выражении 5⋅(3+7) сначала будет вычислено сложение в скобке, и лишь потом умножение: 5⋅(3+7)=5⋅10=50.
Однако если мы имеем дело с алгебраическим выражением, содержащим переменную — например таким:
2(x−3)
– то вычислить значение в скобке не получается, мешает переменная. Поэтому в таком случае скобки «раскрывают», используя для этого соответствующие правила.
Поэтому в данном случае 6 :2(1+2) это арифметика епта и поэтому сначала считаются скобки т.е 1+2 =3 6:2=3 и 3*3=9
а то что вы написали, даже если поставить дробь вместо деления т.е. правильно
6/2*(1+2)=3*3 или 18/2 как угодно 9. И не путайте алгебраическое выражение с неизвестными где число возле скобок без умножения и скобки воспринимаются как единое целое с арифметикой.
И все споры тут ниочем , считать 2(1+2) единым целым или нет , нет не считать. А считать только если 2(1а+2b).
И 6:2*(1+2)=9 это тоже уравнение только без неизвестных!
Пример очень нашумевший, конечно. Сейчас в уже в соц сетях обсуждают по полной!:)).
Рассуждая о правильном ответе в математическом выражении 6:2(1+2), нужно применять основы математической методологии!
Возьмем два примера 6:2(1+2) и 6:2*(1+2). В этих выражениях в правой части после знака деления мы видим два отличающихся визуально действия 2(1+2) и 2*(1+2). В чем здесь принципиальная разница помимо того, что мы видим визуально. В выражении 2*(1+2) мы видим два параметра 2 и (1+2), разделенные знаком «умножение». Эти два параметра независимы друг от друга! То есть, посчитав выражение в скобках, общее выражение можно написать в виде — 2*3. То есть оно тождественно 2* (1+2). Говоря методологически — мы не обязаны после совершенных действий в скобках сразу умножать результат на 2. То есть 2*(1+2)=2*3. Эти элементы (параметры) 2 и (1+2) могут взаимодействовать друг с другом посредством какой-то математической операции, в данном случае «умножение» (*). Но при этом они друг от друга не зависимы. Так как они могут быть записаны в пределах одного выражения разными способами, они обособлены и имеют полноценное право на взаимодействие с любыми элементами в пределах каких-либо правил математического взаимодействия. То есть подставив выражение 2*(1+2) в выражение 6:2*(1+2), оно начинает «подчиняться» вновь появившимся правилам взаимодействия! После действий в скобках начинается деления 6 на 2, и только потом умножение на результат в скобках. То есть срабатывает «независимость» 2-йки от других элементов выражения, и дальнейшие действий подчиняются базовым законам исчисления!. Значит ответ в данном случае — 9.
А теперь посмотрим на выражение 2(1+2) . В чем принципиальное отличие от предыдущего примера. Отличие практически фундаментально!! В отсутствии знака «умножение» цифра 2 перед скобкой превращается в коэффициент, который может иметь как усиливающий эффект так и понижающий. То есть 2-ка имеет прямое влияние на скобку. Выражение в скобках уже априори «усилено» 2-кой перед скобкой. Результат выражения в скобках АВТОМАТИЧЕСКИ ( в данном случае) «усиливается» в 2 раза. То есть, как только мы посчитали (1+2), то оно сразу превращается в 6-ку. Выражение 2(1+2) едино, оно не зависимо от других выражений. Все действия в рамках этого выражения имеют приоритет перед другими действиями в более широких арифметических пределах! То есть, подставив выражение 2(1+2) в выражение 6:2(1+2) — мы получаем 6:6=1. И ни как иначе.
___________________________________
выводы:
1. Если в условии задачи стоит пометка типа «выполните простое арифметическое действие..», либо явно стоит знак «умножение» — то считать нужно по правилу «слева на право». То есть ответ будет 9.
2. Если нет ни каких пометок и комментариев и нет знака «умножение», то считать нужно по второму принципу, и ответ будет 1. Как говорил один мудрый профессор: — С(А+В) и С*(А+В) — это разные вещи!!
3. Ставьте дополнительные скобки для подстраховки!:).
P.s. «Правильная» постановка задачи ведет к «нужному» решению!:))
Я выше постарался ответить на «Никак иначе». Еще «иначе» получилось. По согласно переместительному свойству умножения: 2(2+1)=(2+1)*2 (перед числом ВСЕГДА ставится знак умножения). А теперь подставьте в исходный пример и посмотрите что вышло.
Если вы ставите знак умножения, то должны написать скобки 6:2(2+1) = 6:((2+1)×2) = 6:(3×2) = 6:6 = 1.
Цитата из Методики преподавания алгебры в восьмилетней школе Репьева В. В., стр. 81:
«Если бы в делителе были записаны знаки умножения, то пришлось бы написать:
a : (b×c×d).
… при делении числа на произведение, в котором опущены знаки умножения, можно не заключать делитель в скобки, т.е. писать:
a : bcd.»
https://russianclassicalschool.ru/biblio/11_sr_sk_metod_algebra.pdf
Откройте хотя бы онлайн калькулятор от Гугл. Введите выражение без знака умножения и посмотрите на ответ. Удивительно, но ответ = 9.
Возможно, Гугл и его команда не знает Ваше правило про «усиление» в случае отсутствия знака умножения, а также не знает изречение «мудрого профессора».
Вот и считает буржуйский сервис неправильно.
А помимо гугла еще сотня онлайн инженерных калькуляторов не знают правила «усиления», и тоже выдают ответ 9ку. Безграмотные, что тут сказать.
чтож давайте мерятся буржуазными калькуляторами 🙂
давайте возьмем инженерный калькулятор из Виндовс10.
Он даже не позволяет ввести выражение вида 6:2(2+1) так как оно может иметь разночтение и поэтому он считает такое выражение недопустимым.
Итак кто круче? Гугл или Мелкософт? Ларри или Билли? :)))
Источник