§ 18. Управление исполнителем Чертёжник
Ключевые слова:
- исполнитель Чертёжник
- абсолютное смещение
- относительное смещение
- вспомогательный алгоритм
- основной алгоритм
- цикл n раз
Знакомимся с Чертёжником
Исполнитель Чертёжник предназначен для построения рисунков на координатной плоскости.
При задании точек этой координатной плоскости, в отличие от того, как это принято в математике, координаты хну разделяются запятой. Например, координаты выделенной на рис. 63 точки будут записаны так: (1, 1).
Чертёжник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остаётся след — отрезок от предыдущего положения пера до нового. При перемещении поднятого пера никакого следа на плоскости не остаётся. В начальном положении перо Чертёжника всегда поднято и находится в точке (0, 0).
По команде поднять перо Чертёжник поднимает перо. Если перо уже было поднято, Чертёжник игнорирует эту команду: он не меняет положение пера и не сообщает об отказе. Иначе говоря, каким бы ни было положение пера до команды поднять перо, после этой команды оно будет поднятым.
Точно так же, независимо от первоначального положения, после выполнения команды опустить перо оно оказывается опущенным, т. е. готовым к рисованию.
Рисунки Чертёжник выполняет с помощью команд сместиться в точку и сдвинуться на вектор.
По команде сместиться в точку (а, b) Чертёжник сдвигается в точку с координатами (а, b). На рисунке 64 показаны результаты выполнения команды сместиться в точку (2, 3) при различных положениях пера до этой команды. Видно, что, независимо от предыдущего положения, перо оказывается в точке (2, 3), но длина и направление отрезка, который при этом чертится, могут быть различны. Команду сместиться в точку называют командой абсолютного смещения.
Назовите координаты точек, в которых находился Чертёжник до выполнения команды сместиться в точку (2, 3) (см. рис. 64).
В каком случае в результате выполнения команды сместиться в точку (2, 3) из некотрого показанного на рис. 64 начального положения не будет прочерчен ни один отрезок?
Пусть перо Чертёжника находится в точке (x, у). По команде сместиться на вектор (а, b) Чертёжник отсчитывает а единиц вправо вдоль горизонтальной оси (оси абсцисс), b единиц вверх вдоль вертикальной оси (оси ординат) и сдвигает перо в точку с координатами (х + а; у + b). Таким образом, координаты, указанные в команде, отсчитываются не от начала координат, а относительно текущего положения пера Чертежника. Поэтому команду сместиться на вектор называют командой относительного смещения.
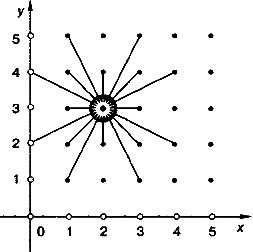
На рисунке 65 показаны результаты выполнения команды сместиться на вектор (2, 3) при различных положениях пера до этой команды. Из рисунка видно, что положение пера после этой команды зависит от его предыдущего положения, зато в результате получаются отрезки, длина и направление которых одинаковы.
В математике направленные отрезки называются векторами, отсюда и происходит название команды.
Назовите координаты точек, в которых находилось перо Чертёжника до выполнения команды сместиться на вектор (2, 3) и куда оно переместилось после выполнения этой команды.
Как будет выполняться команда сместиться на вектор (а, b), если:
Служебные слова нц и кц пишутся одно под другим. Чуть правее между ними записывается повторяющаяся последовательность команд (тело цикла). Число повторений — произвольное целое число. Именно столько раз при выполнении алгоритма будут повторены команды, образующие тело цикла.
Предложите вариант решения задачи о почтовом индексе Красноярска с использованием конструкции повторения.
Можно ли обойтись без вспомогательного алгоритма в следующих ситуациях (рис. 72)?
Источник
Мастер — класс «Формирование творческих способностей учащихся на уроках программирования »
Поиск по этому блогу
Исполнитель «Чертежник»
Чертежник предназначен для построения рисунков, чертежей, графиков на бесконечном листе бумаги. Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след — отрезок от старого положения до нового.
- Показать окно Чертежника (отображение окна Чертежника; по умолчанию окно скрыто)
- Сохранить/Загрузить чертеж. (сохранение созданного чертежа в формате .psk/загрузка ранее сохраненного чертежа из памяти компьютера)
- Очистить чертеж (очистка листа Чертежника)
- Печатать чертеж. (печать созданного чертежа на принтере)
- Вид
- Приблизить/Отодвинуть (настройка масштаба отображения чертежа)
- Показать весь чертеж (автоподбор масштаба, при котором весь чертеж помещается в окне Чертежника)
- Вертикальное/Горизонтальное окно (выбор ориентации окна исполнителя)
- Сетка (настройка шага сетки по каждой оси, ее отображения).
Если убрать верхнюю галочку, то на листе Чертежника линии сетки отображаться не будут.
При квадратной сетке шаг по обеим осям выставляется одинаковым. Если необходимо задать шаг сетки для каждой оси координат свой, то данную галочку необходимо убрать.
Для того, чтобы окно чертежника не перекрывалось окном разработки программы, необходимо кликнуть правой клавишей мыши по заголовку окна Чертежника и в контекстном меню выбрать пункт «Поверх всех окон».
Примечание: рассматриваемый исполнитель можно использовать на уроках математики 5(6) классов при изучении темы «Координатная плоскость».
Результат выполнения команд Чертежника
(Перед началом алгоритма необходимо ОБЯЗАТЕЛЬНО записать «Использовать Чертежник «. Для запуска программы на исполнение нажимаем клавишу F9)
По умолчанию перо Чертежника поднято и расположено в точке (0,0). Переместим перо в точку (5,5) чтобы продемонстрировать разницу между командами сместиться в точку ( вещ x , вещ y ) и сместиться на вектор ( вещ dx , вещ dy ).
Теперь опустим перо и выполним команду сместиться в точку (2,-3 ). В итоге выполнения программы перо Чертежника переместилось из точки (5,5) в точку (2,-3), оставив след на листе
Теперь заменим команду сместиться в точку (2,-3 ) на сместиться на вектор (2,-3 ) . В результате перо чертежника переместилось в точку (7,2).
Изменим цвет линии на красный, добавив в начало программы команду установить цвет(«красный»)
С помощью команды надпись (1, «красная линия» ) добавим подпись к чертежу. Значение ширины знакоместа может также принимать дробные значения (например 2.5).
Источник
Исполнитель Чертежник
Круг решаемых задач: предназначен для построения рисунков, чертежей и графиков, состоящих из прямых линий.
Среда исполнителя: Чертежник действует на координатной плоскости. Начальное положение пера в начале координат (в точке с координатами (0,0)).
Система команд исполнителя:
сместиться в точку (арг вещ х,у),
сместиться на вектор (арг вещ х,у),
выбрать чернила (лит наименование цвета) .
В команде сместиться в точку в качестве (х,у) выступают абсолютные значения координат, а сместиться на вектор — значения приращений по соответствующим осям. Т.е. при команде сместиться в точку (x,y) Чертёжник из точки с координатами (a, b) в точку с координатами (x, y). При команде сместиться на вектор (x,y) Чертёжник из точки с координатами (a, b) в точку с координатами (a+x, b+y). Если числа х, у положительные, значение соответствующей координаты увеличивается, если отрицательные – уменьшается. Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на вектор (2, –3) переместит Чертёжника в точку (6, –1).
При перемещении опущенного пера за ним остается след — отрезок от старого положения пера до нового, а при перемещении с поднятым пером следа не остается.
Команда выбрать чернила задает цвет пера: ”черный”, ”белый”, ”красный”, ”оранжевый”, ”желтый”, ”зеленый”, ”голубой”, ”синий”, ”фиолетовый”. По умолчанию используется черный цвет. Название цвета пишется без кавычек.
При смещении на вектор изменяются координаты х, у на числа, указанные в команде
Линейные алгоритмы представляют собой последовательность команд, следующих друг за другом. Рассмотрим на примере трапеции.
Запишем алгоритм рисования трапеции в абсолютных величинах, используя команду сместиться в точку (рис. 1).
Но если мы захотим переместить эту трапецию из первой четверти во вторую, то нам придется изменять все координаты, что не рационально, поэтому воспользуемся командой сместиться на вектор (рис.2). И далее для составления алгоритмов будем пользоваться ей.
Во втором варианте для перемещения трапеции необходимо поменять координаты только первой команды, что эффективнее чем в первом варианте.
рис. 1
рис. 2
Задача : Составим алгоритм рисования квадрата. После рисования вернем Чертежника в исходную позицию.
Для перемещения можно использовать две команды — «сместиться в точку» и «сместиться на вектор». Запишем, для примера, два алгоритма — в одном будем использовать только первую команду, в другом только вторую.
Прежде чем Чертежник начнет рисовать (опустит перо) нужно сместится к место рисования. После рисования нужно снова поднять перо и перейти в начало координат (так требуется по условию). Рисовать будем с нижней левой точки по часовой стрелке.
Пример 1
. сместиться в точку (2,1)
. сместиться в точку (2,4)
. сместиться в точку (5,4)
. сместиться в точку (5,1)
. сместиться в точку (2,1)
. сместиться в точку (0,0)
Пример 2
. сместиться на вектор (2,1)
. сместиться на вектор (0,3)
. сместиться на вектор (3,0)
. сместиться на вектор (0,-3)
. сместиться на вектор (-3,0)
. сместиться на вектор (-2,-1)
Обычно в программах используют эти две команды одновременно, все зависит от условий задачи и предпочтения составителя алгоритма. Например, можно записать алгоритма так:
Пример 3
. сместиться в точку (2,1)
. сместиться на вектор (0,3)
. сместиться на вектор (3,0)
. сместиться на вектор (0,-3)
. сместиться на вектор (-3,0)
. сместиться в точку (0,0)
Обратите внимание — исполнитель выполняет действия последовательно, одно за другим в том порядке, в котором они следуют.
При создании «средних» по размеру программ используется структурное программирование, идея которого заключается в том, что структура программы должна отражать структуру решаемой задачи, чтобы алгоритм решения был ясно виден из исходного текста. Программа разбивается на множество подпрограмм (вспомогательных алгоритмов), каждая из которых выполняет какое-то действие, предусмотренное исходным заданием.
Комбинируя вспомогательные алгоритмы, удается сформировать итоговый алгоритм используя блоки кода (подпрограммы), имеющих определенную смысловую нагрузку. Обращаться к ним, можно по их имени. Очень важная характеристика вспомогательных алгоритмов — это возможность их повторного использования.
Там, где какие-то части программы повторяются (используются) несколько раз, удобно использовать вспомогательные алгоритмы.
Обратите внимание — если нам потребуется изменить алгоритм так, чтобы рисовались треугольники со стороной 4, а не 2, то при использовании вспомогательного алгоритма количество правок заметно уменьшается.
Примечание: все алгоритмы в программе на КуМире пишутся друг за другом, для удобства их можно отделять пустой строкой, главным считается алгоритм записанный первым, именно он начинает выполняться после запуска программы.Использованный нами подход облегчает программирование сложных задач. Задача разбивается на более простые подзадачи. Решение каждой оформляется в виде вспомогательного алгоритма, а основной алгоритм организует связку между ними.
Источник
Что значит опустить перо
Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды:
Сместиться на вектор (а, b) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали.
Запись: Повторить 5[Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз.
Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм:
Сместиться на вектор (5,2)
Сместиться на вектор (-3, 3)
Повторить 3[Сместиться на вектор (1,0)]
Сместиться на вектор (3, 1)
На каком расстоянии от начала координат будет находиться исполнитель Чертежник в результате выполнения данного алгоритма?
Конечная точка будет обладать координатами по оси x и y. Эти координаты можно складывать независимо друг от друга.
Найдём значение x: 5 — 3 + 1 + 1 + 1 + 3 = 8.
Найдём значение y: 2 + 3 + 1 = 6.
Расстояние от начала координат находится по формуле: , поэтому
.
Источник