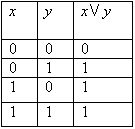Примеры решения задач «Алгебра высказываний»
Примеры решения задач «Алгебра высказываний»
№1.
Определите значения следующих логических переменных:
1) А = « Два умножить на два равно пяти»
2) В = «Всякий квадрат есть параллелограмм»
3) С = «Всякий параллелограмм есть квадрат»
Ответ: А =0, В = 1, С = 0
№2.
Определите значение истинности следующих высказываний:
1) Высказывание «10 делится на 2 и 5 больше 3»
2) Высказывание «10 делится на 2 и 5 не больше 3»
3) Высказывание «10 не делится на 2 и 5 больше 3»
4) Высказывание «10 не делится на 2 и 5 не больше 3»
Ответ:
1) истинное высказывание (1/\1=1)
2) ложное высказывание(1/\0=0)
3) ложное высказывание (0/\1=0)
4) ложное высказывание (0/\0=0)
№3.
Запишите логические функции, соответствующие данным сложным высказываниям (в задании использовались строки из стихов А. С. Пушкина):
1). Мне вас не жаль, года весны моей.
2). На холмах Грузии лежит ночная мгла;
Шумит Арагва предо мною…
3). Унынья моего ничто не мучит, не тревожит.
4). Мне не спится, не огня;
Всюду мрак и сон докучный.
Ответ:
1) F(A) = не А
2) F(A, В) = А и В
3) F(A, В) = не А и не В
4) F(A, В, C, D) = не А и не В и С и D
№4.
Представьте данное высказывание «Число 6 делится на 2, и число 6 делится на 3» в виде логической формулы.
Решение: Обозначим через А простое высказывание «Число 6 делится на 2» — истинное высказывание, через В — «Число 6 делится на 3»- истинное высказывание. Простые высказывания соединены связкой и (конъюнкция), очевидно логическая формула имеет вид А /\ В. Ее значение ((1/\1=1) — истина.
№5.
Даны два высказывания: А= <3+2=5>и B=<круг имеет форму прямоугольника>. Определите, чему равны составные высказывания:
Ответ:
1) 0
2) 1
№6.
Определите истинность составного высказывания: ( ¬ А /\ ¬ B) /\ (C \/ D), состоящего из простых высказываний:
Решение:
Сначала устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.
Затем определим истинность составного высказывания, используя таблицы истинности логических операций: (ø1/\ø0) /\ (1\/ 0) = (0 /\1) /\ (1 \/ 0) = 0
Ответ: ( ¬ 1/\ ¬ 0) /\ (1\/ 0) = (0 /\1) /\ (1\/ 0) = 0 — составное высказывание ложно.
№7.
Определите истинность составного высказывания:
«(2 * 2 = 4 /\ 3 * 3 = 10) \/ (2 * 2 = 5 /\ 3 * 3 = 9)» .
Решение
Замените простые высказывания логическими переменными и установите их истинность или ложность:
А: «2*2 = 4» — истинно (1),
В: «3*3 = 10 — ложно (0),
С: «2*2 = 5» — ложно (0),
D: «3*3 = 9» — истинно (1).
Замените также логические связки «и» и «или» операциями логического умножения и логического сложения. Тогда составное высказывание примет вид следующего логического выражения: (А /\ В) \/ (С /\ D).
Подставьте вместо логических переменных их логические значения и определите истинность составного высказывания, используя таблицы истинности логических функций:
(1/\ 0) \/ (0/\1) = 0 + 0= 0.
Ответ: составное высказывание ложно.
Источник
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2 n , где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
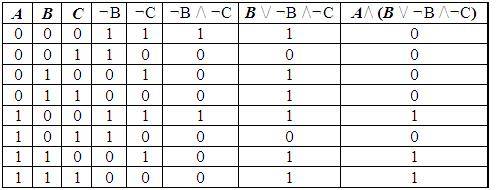
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2 n , m=2 2 =4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
Источник
Определение значения истинности высказываний. Построение составных высказываний
Тема программы: Высказывания и операции над ними.
1) Обобщить теоретические знания по теме: «Высказывания и операции над ними».
2) Рассмотреть алгоритмы решений заданий теме «Высказывания и операции над ними», решить задачи.
3) Формировать умение прогнозировать собственную деятельность, умение организовать свою деятельность и анализировать ее.
Время выполнения: 1 час.
Теоретические основы
Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».
Примеры высказываний.
1) Москва стоит на Неве.
2) Лондон — столица Англии.
3) Сокол не рыба.
4) Число 6 делится на 2 и на 3.
Высказывания 2), 3), 4) истинны, а высказывание 1) ложно.
Очевидно, предложение «Да здравствует Россия!» не является высказыванием.
Различают два вида высказываний.
Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если . то . », «тогда и только тогда», принято называть сложными или составными.
Так, высказывание 3) получается из простого высказывания «Сокол — рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на З», соединенных союзом «и».
Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Элементарные высказывания обозначаются малыми буквами латинского алфавита: х, у, z, . а, b, с, . ; истинное значение высказывания цифрой 1, а ложное значение — буквой цифрой 0.
Если высказывание а истинно, то будем писать а = 1, а если а ложно, то а = 0.
Логические операции над высказываниями
Отрицанием высказывания х называется новое высказывание 
, которое является истинным, если высказывание х ложно, и ложным, если высказывание х истинно.
Отрицание высказывания х обозначается и читается «не х» или «неверно, что х».
Логические значения высказывания можно описать с помощью таблицы.
Таблицы такого вида принято называть таблицами истинности.
Пусть х высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание 
, которое называется двойным отрицанием высказывания х. Ясно, что логические значения высказываний х и совпадают.
Например, для высказывания «Путин президент России» отрицанием будет высказывание «Путин не президент России», а двойным отрицанием будет высказывание «Неверно, что Путин не президент России».
Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний х и у обозначается символом х&у (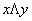 
, ху ) , читается «х и у» . Высказывания х и у называются членами конъюнкции.
Логические значения конъюнкции описываются следующей таблицей истинности:
Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.
Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у» . Высказывания х, у называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:
В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле.
Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у — ложно, и истинным во всех остальных случаях.
Импликация высказываний х, у обозначается символом 
, читается«если х, то у» или «из х следует у». Высказывание х называют условием или посылкой, высказывание у — следствием или заключением, высказывание следованием или импликацией.
Логические значения операции импликации описываются следующей таблицей истинности:
Употребление слов «если . то . » в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х . Употребление слов «если . то . » в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если х, то у». Если при этом известно, что х истинно и доказана истинность импликации , то мы вправе сделать вывод об истинности заключения у .
Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквивалентность высказываний х, у обозначается символом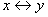 
, читается«для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквивалентности.
Логические значения операции эквивалентности описываются следующей таблицей истинности:
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Практические задания
1. Установить логическую структуру следующих предложений и записать их на языке логики высказываний:
- Если металл нагревается, он плавится.
- Неправда, что философские споры неразрешимы.
- Деньги — продукт стихийного развития товарных отношений, а не результат договоренности или какого-либо иного сознательного акта.
2. Записать логической формулой следующие высказывания:
а) если на улице дождь, то нужно взять с собой зонт или остаться дома;
б) если — прямоугольный и стороны — равны, то
3. Проверить истинность высказывания:
4. Проверить истинность высказывания:
а) Чтобы завтра пойти на занятия, я должен встать рано. Если я сегодня пойду в кино, то лягу спать поздно. Если я лягу спать поздно, то встану поздно. Следовательно, либо я не пойду в кино, либо не пойду на занятия.
б) Я пойду либо в кино, либо в бассейн. Если я пойду в кино, то получу эстетическое удовольствие. Если я пойду в бассейн, то получу физическое удовольствие. Следовательно, если я получу физическое удовольствие, то не получу эстетического удовольствия.
5 
. На вопрос: «Кто из трех студентов изучал дискретную математику?» получен верный ответ: «Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий». Кто изучал дискретную математику?
6. Определите, кто из четырех студентов сдал экзамен, если известно:
если первый сдал, то и второй сдал;
если второй сдал, то третий сдал или первый не сдал;
если четвертый не сдал, то первый сдал, а третий не сдал;
если четвертый сдал, то и первый сдал.
Контрольные вопросы
1. Какие элементы входят язык логики?
2. Какие способы установления общезначимости формулы логики вы знаете?
Список литературы
| 1.Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с. |
| 2.Варпаховский Ф.Л. Элементы теории алгоритмов. — М., Просвещение, 1970. — 25 с. (МГЗПИ) |
| 3.Гуц А.К. Математическая лоrика и теория алrоритмов. — Омск: Издательство Наследие. Диалог-Сибирь, 2003. — 108 с. |
| 4.Босс В. Лекции по математике. Т. 6: От Диофанта до Тьюринга. — М.: КомКнига, 2006. — 208 с. |
| 5.Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. — 216 с. |
Практические занятия № 10-11
Тема программы: Формулы алгебры высказываний.
Дата добавления: 2018-02-28 ; просмотров: 9595 ; Мы поможем в написании вашей работы!
Источник
