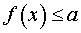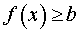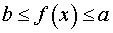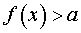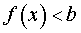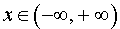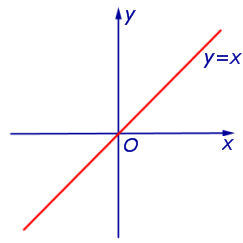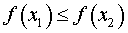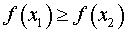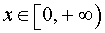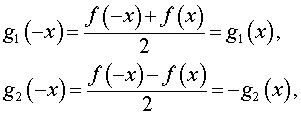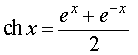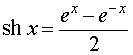Что значит ограниченная задача

5 способов ставить задачи, чтобы их понимали и выполняли в срок

Когда задачи не выполняются, виноват часто не только тот, кто их делал, но и тот, кто ставил. Ведь от правильной постановки напрямую зависит качество и эффективность выполнения. Не приложили инструкций, не объяснили целей и ожидаемых результатов, не дали инструментов – вот у сотрудника или подрядчика и не получилось сделать все, как нужно.

Сложность еще и в том, что часто с позиции постановщика сложно оценить, какая именно информация, данные и инструменты нужны исполнителю. Первому кажется, что все очевидно, а для второго это не так. Чтобы этого избежать, можно использовать методы постановки задач, которые помогают разложить все по полочкам, не упустить ничего важного и повысить шансы на успех. В статье рассмотрим 5 таких методов с примерами.

SMART

Один из самых популярных подходов, который позволяет собрать воедино всю необходимую информацию и сформулировать задачу максимально четко и понятно. Изначально использовался для постановки целей, но подходит и для задач.

Буквы аббревиатуры обозначают критерии правильно поставленной задачи:

Time bound – ограниченная во времени.

Важно, чтобы задача отвечала всем пяти критериям

Пример. Допустим, заказчику нужно получить больше трафика из контекстной рекламы в высокий сезон – с июня по август. Для этого он ставит задачу исполнителю – подрядчику по контекстной рекламе. Чтобы она соответствовала SMART-критериям, ее можно сформулировать так:

Увеличить трафик с контекстной рекламы на 20% к 1.06.2020 за счет запуска РСЯ, Google Ads и YouTube.

В такой формулировке задача:

конкретная – показывает, какой нужно получить результат и каким способом;

измеримая – указан процент, на который нужно увеличить трафик;

достижимая – учитывая, что РСЯ, Google Ads и YouTube еще даже не запускали;

значимая – компании важно получить больше трафика в сезон, чтобы максимизировать прибыль;

ограниченная во времени – указан срок.

Модель ориентирована на постановку задач программистам, так как работает по принципам алгоритма, но и для взаимодействия с сотрудниками и подрядчиками других специальностей тоже подойдет. Особенно полезна для работы с новичками, так как раскладывает задачу и процесс работы над ней по полочкам.

В отличие от метода SMART, здесь буквы аббревиатуры обозначают не критерии, а главы ТЗ и отчасти этапы работы над задачей:

Test1 – какой результат нужно получить или что конкретно сделать;

Operation – какие действия нужно выполнить, чтобы получить результат;

Test2 – как мы поймем, что двигаемся к результату;

Exit – как мы поймем, что достигли результата.

Такой подход помогает исполнителю лучше понять задачу, потому что показывает, как достигнуть результата и убедиться, что получили именно то, что нужно.

Четкий алгоритм постановки задачи по TOTE

Пример. Специалист по контекстной рекламе взял в помощники новичка и решил начать практику с самого простого, например с составления объявлений. Такая задача, поставленная по TOTE, может выглядеть так:

Подготовить объявления для рекламной кампании Ателье

T1: Нужно составить объявления в соответствии с согласованной с клиентом концепцией (в файле) по шаблону (прилагаю) и нашим правилам (в чек-листе). Объявления должны содержать по два заголовка, тексты, быстрые и отображаемые ссылки.

O: Чек-лист задачи:

1. Изучить концепцию и чек-лист по созданию объявлений;

2. Скопировать в шаблон ключевые фразы и заполнить все поля для каждой;

3. Проверить объявление по чек-листу и на соответствие ограничениям Директа;

T2: Чтобы не переделывать, делай все в этой последовательности.

E: Результатом будет заполненный и согласованный шаблон, готовый к загрузке в Яндекс.Директ.

HD-RW-RM

Способ позволяет дать исполнителю всю необходимую информацию, не забыв ничего важного. Отчасти пересекается со SMART, но учитывает не критерии, а информационные блоки ТЗ.

Буквы аббревиатуры обозначают разделы шаблона, по которому удобно заполнять задачу:

Header – заголовок, отвечает на вопрос «Что нужно сделать»;

Description – описание, погружает в контекст задачи и детали;

Result – результат, описывает критерии, по которым будем определять, что задача выполнена;

Way – путь, может показывать, с чего начать, или содержать четкий алгоритм с точками контроля;

Redline – время и приоритет, выставляет сроки и показывает, насколько задача важна;

Motivation – мотивация, объясняет, зачем результат нужен поставщику, исполнителю и другим заинтересованным сотрудникам.

Главное отличие от других методов – в блоке «Мотивация». Понимая, зачем это нужно, исполнитель может более ответственно подойти к выполнению задачи.

Шаблон для постановки таких задач может выглядеть так

Пример. Небольшая команда специалистов по контекстной рекламе растет, и, чтобы масштабироваться безболезненно и поддерживать уровень качества на каждом проекте, нужно стандартизировать процессы. Руководитель ставит одному из самых опытных членов команды задачу описать процесс настройки кампании в Яндекс.Директе. Важно учесть все нюансы, ведь от четкости процессов может зависеть доход всей команды в целом и каждого специалиста в отдельности.

Поставленная по методу HD-RW-RM, задача может выглядеть так:

Стандартизировать настройку кампаний в Яндекс.Директе

Описать процесс настройки кампании в Яндекс.Директе

Нам нужно стандартизировать все процессы работы над проектами. Начать решили с настройки кампаний в Директе, так как таких задач сейчас в работе больше всего. Нужен четкий алгоритм, по которому смогут работать и опытные сотрудники, и новички.

Результатом станет пошаговая инструкция в Google Docs и чек-лист, который мы сможем прикладывать к таким задачам в таск-менеджере.

Начни со своего опыта – опиши алгоритм, по которому настраиваешь сам. Собери все моменты, в которых можно ошибиться. Потом обсуди с парой опытных ребят. Возможно, они подскажут, как сделать эффективнее какие-то этапы. Покажи 2-3 новичкам, чтобы собрать их вопросы. Доработай и согласуем.

Время и приоритет

У задачи первый приоритет после клиентских проектов. Будет здорово, если сможем запустить работу по новому процессу через месяц, 25 июля.

Мы продолжаем расти. Этот алгоритм поможет делать кампании быстрее без потери качества и не упускать важных деталей. А значит, мы сможем взять дополнительные проекты и все вместе будем зарабатывать больше.

Задача важная, поскольку влияет на репутацию и прибыль, но сотрудник опытный, поэтому ему можно не расписывать весь процесс по шагам.

Кстати, получать больше прибыли от ведения контекстной рекламы можно не только за счет роста клиентской базы, но и с помощью партнерских программ. Например, участники партнерской программы Click.ru получают до 18% от рекламного оборота клиентов.

CLEAR

Методику разработал канадский бизнес-тренер и гребец Адам Крик в качестве альтернативы модели SMART. В отличие от нее, CLEAR позволяет ставить более гибкие задачи, которые могут изменяться в зависимости от обстоятельств.

Буквы аббревиатуры обозначают критерии, которым должна соответствовать правильно поставленная задача:

Collaborative – командная, мотивирует сотрудников работать вместе;

Limited – ограниченная, по аналогии со SMART – достижимая и ограниченная во времени;

Emotional – эмоциональная, интересна исполнителям;

Approachable – доступная, можно разбить на мелкие подзадачи;

Refinable – гибкая, может изменяться в процессе выполнения.

Первый критерий подразумевает, что метод лучше использовать, когда нужно поставить задачу нескольким сотрудникам или группе исполнителей, иначе в нем теряется смысл.

Критерии другие, принцип тот же

Пример. Системы контекстной рекламы регулярно выпускают обновления и новые инструменты. Чтобы оставаться в тренде и не растерять клиентов, в отделе контекстной рекламы решили поставить регулярную задачу для всех специалистов: ежемесячно изучать обновления, проверять, на каких проектах они могут быть полезны, и направлять предложения по оптимизации клиентам.

Вот как можно сформулировать эту задачу по CLEAR:

Направлять клиентам предложения по подключению новых инструментов рекламных систем до 10 числа каждого месяца.

Так она соответствует методике:

командная – задачу поставили всему отделу, сотрудники могут помочь друг другу разобраться в обновлениях и составить предложения;

ограниченная – она достижима и имеет сроки (до 10 числа);

эмоциональная – выходит за рамки стандартных процессов и позволяет проявить свои навыки и знания в маркетинге;

доступная – можно разбить на подзадачи: изучить обновления, проанализировать проекты в работе и т. д.;

гибкая – в один месяц Яндекс.Директ выпускает обновления одно за другим, в другой – едва меняет что-то по мелочи.

Еще одна альтернатива методу SMART, разработанная Массачусетским технологическим институтом. Эта методика также ориентирована на командную работу и амбиции исполнителей, поэтому вряд ли подойдет для рядовых задач вроде сбора семантики или анализа площадок в РСЯ.

Так же как в SMART и CLEAR, буквы аббревиатуры обозначают критерии задачи:

Frequently discussed – часто обсуждаемая, о задаче в команде постоянно говорят, чтобы не упустить ее из виду;

Ambitious – амбициозная, выполнимая, но не слишком легкая, чтобы могла вдохновить исполнителей на достижение большего;

Specific – конкретная, по аналогии со SMART;

Transparent – прозрачная, сама задача и цель, для достижения которой ее нужно сделать, видны всей команде.

Методика помогает ставить и работать с важными для компании или проекта задачами так, чтобы они оставались в фокусе и выполнялись качественно.

Пожалуй, выбирать между SMART, CLEAR и FAST можно в зависимости от типа и важности задачи, а также от того, кому она адресована

Пример. В агентстве решили повысить уровень клиентского сервиса за счет более прозрачных и понятных отчетов по контекстной рекламе. Перед отделом стоит глобальная задача: подобрать подходящий инструмент и перенести в него всю клиентскую отчетность.

По FAST задачу можно сформулировать так:

Подобрать и внедрить до 1 июня систему визуализации данных с возможностью строить динамические отчеты по контекстной рекламе, чтобы сделать отчетность быстрее для специалистов и понятнее для клиентов.

Пройдемся по критериям:

часто обсуждаемая – задача затрагивает всех сотрудников отдела, поэтому ее будут обсуждать;

амбициозная – она непростая, потому что глобальная, но выполнима;

прозрачная – всем сотрудникам понятно, что сделать (подобрать и внедрить) и зачем это нужно (ускорить процессы и сделать отчеты понятнее).

7 полезных инструментов для постановки задач

Выбрать какой-то один метод и оттачивать его или использовать разные способы для постановки задач разной сложности сотрудникам разного уровня – решать вам. В любом случае все задачи нужно где-то фиксировать. Поэтому делимся подборкой таск-менеджеров, в которых можно ставить задачи по любой из этих методологий. Выбирайте, исходя из потребностей и размеров вашей команды:

Источник

Свойства функций. График функции

Содержание

Ограниченные и неограниченные функции

Монотонные и строго монотонные функции

Четные и нечетные функции

Периодические и непериодические функции. Период функции

График функции. Свойства графиков четных, нечетных, периодических функций

Ограниченные и неограниченные функции

Обозначим буквой X некоторое множество чисел, входящих в область определения D ( f ) функции y = f (x) .

ОПРЕДЕЛЕНИЕ 1. Функцию y = f (x) называют ограниченной сверху на множестве X , если существует такое число a , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 2. Функцию y = f (x) называют ограниченной снизу на множестве X , если существует такое число b , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 3. Функцию y = f (x) называют ограниченной на множестве X , если существуют такие числа a и b , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 4. Функцию y = f (x) называют неограниченной сверху на множестве X , если для любого числа a существует такой x из множества X , для которого выполнено неравенство

ОПРЕДЕЛЕНИЕ 5. Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого числа b существует такой x из множества X , для которого выполнено неравенство

ОПРЕДЕЛЕНИЕ 6. Функцию y = f (x) называют неограниченной на множестве X , если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.

Проиллюстрируем эти определения следующими примерами.

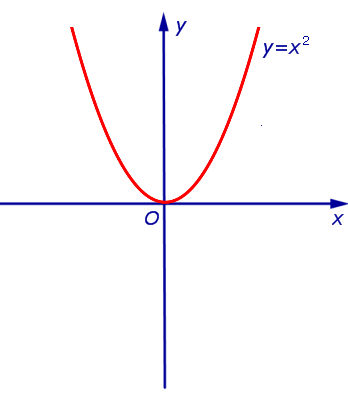
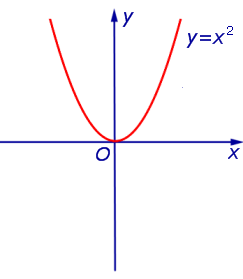
ПРИМЕР 1. Функция y = x 2 (рис. 1) является ограниченной снизу и неограниченной сверху на множестве

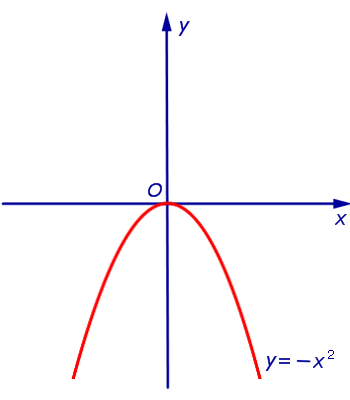
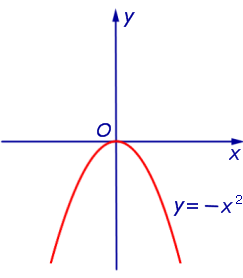
ПРИМЕР 2. Функция y = – x 2 (рис. 2) является ограниченной сверху и неограниченной снизу на множестве

ПРИМЕР 3. Функция y = x (рис. 3) неограничена сверху и неограничена снизу на множестве

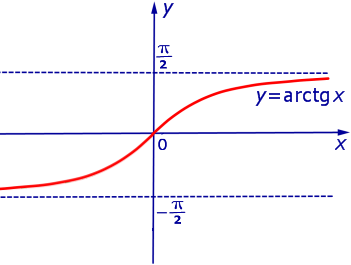
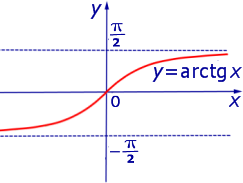
ПРИМЕР 4. Функция y = arctg x (рис. 4) ограничена на множестве

Монотонные и строго монотонные функции

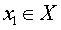
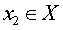
ОПРЕДЕЛЕНИЕ 7. Функцию y = f (x) называют возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ЗАМЕЧАНИЕ 1. Возрастающие функции также называют неубывающими функциями.

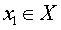
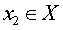
ОПРЕДЕЛЕНИЕ 8. Функцию y = f (x) называют убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ЗАМЕЧАНИЕ 2. Убывающие функции также называют невозрастающими функциями.

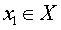
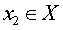
ОПРЕДЕЛЕНИЕ 9. Функцию y = f (x) называют строго возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

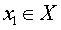
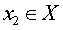
f (x₁) ОПРЕДЕЛЕНИЕ 10. Функцию y = f (x) называют строго убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ОПРЕДЕЛЕНИЕ 11. Возрастающие и убывающие функции называют монотонными, строго возрастающие и строго убывающие функции называют строго монотонными.

ПРИМЕР 5. Функция y = x 2 (рис. 1) является строго убывающей функцией на множестве и строго возрастающей на множестве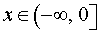

ПРИМЕР 6. Функция y = – x 2 (рис. 2) является строго возрастающей функцией на множестве и строго убывающей на множестве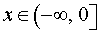

ПРИМЕР 7. Функция y = x (рис. 3) является строго возрастающей функцией на множестве

ПРИМЕР 8. Функция y = arctg x (рис. 4) является строго возрастающей на множестве

Четные и нечетные функции

ОПРЕДЕЛЕНИЕ 12. Функцию y = f (x) , определенную на множестве X , называют четной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство

ОПРЕДЕЛЕНИЕ 13. Функцию y = f (x) , определенную на множестве X , называют нечетной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство

ПРИМЕР 9. Функции y = x 2 и y = – x 2 являются четными функциями (рис. 1 и рис. 2), а функции y = x и y = arctg x являются нечетными функциями (рис. 3 и рис. 4).

ПРИМЕР 10. Примерами функций, которые не являются ни четными, ни нечетными функциями, являются показательные и логарифмические функции.

УТВЕРЖДЕНИЕ. Любую функцию y = f (x) , определенную на симметричном относительно точки x = 0 множестве X , можно представить в виде суммы четной и нечетной функций.

ДОКАЗАТЕЛЬСТВО. Рассмотрим две функции:

сумма которых равна f (x) , и заметим, что функция g₁ (x) является четной функцией, а функция g₂ (x) является нечетной функцией. Действительно,

что и завершает доказательство утверждения.

ЗАМЕЧАНИЕ 3. Раскладывая функцию y = e x в сумму четной и нечетной функций, получаем:

Функцию g₁ (x) называют гиперболическим косинусом и обозначают ch x :

Функцию g₂ (x) называют гиперболическим синусом и обозначают sh x :

Таким образом, справедливо равенство

Периодические и непериодические функции. Период функции

ОПРЕДЕЛЕНИЕ 14. Число называют периодом функции y = f (x) , если для любого числа числа x + T и x – T также принадлежат области определения D ( f ) и справедливы равенства

ОПРЕДЕЛЕНИЕ 15. Если функция имеет период, то ее называют периодической. Если же у функции периода нет, то ее называют непериодической.

ЗАМЕЧАНИЕ 4. Если число T является периодом некоторой функции, то и число kT , где k – любое целое число, отличное от нуля, также является периодом этой функции.

ПРИМЕР 11. Функции y = sin x и y = cos x являются периодическими функциями с периодом 2π , функции y = tg x и y = ctg x являются периодическими функциями с периодом π .

ПРИМЕР 12. Показательные, логарифмические и степенные функции являются непериодическими функциями.

График функции. Свойства графиков четных, нечетных, периодических функций

Рассмотрим плоскость с заданной прямоугольной системой координат Oxy .

ОПРЕДЕЛЕНИЕ 16. Графиком функции y = f (x) называют множество всех точек, координаты которых имеют вид (x; f (x)) , где .

ЗАМЕЧАНИЕ 6 . График периодической функции не изменяется при сдвиге вдоль оси абсцисс Ox на период вправо или влево (см., например, раздел «Графики тригонометрических функций» нашего справочника). Поэтому для того, чтобы построить график периодической функции с периодом T , достаточно построить график этой функции на любом отрезке оси абсцисс Ox длины T , а затем сдвигать его влево и вправо на расстояния nT , где n – любое натуральное число.

Источник