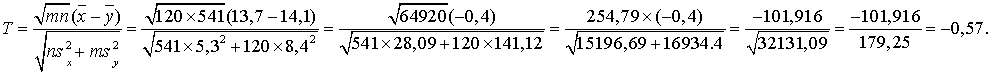Выборка
Материал из MachineLearning.
Содержание
Выборка (sample, set) — конечный набор прецедентов (объектов, случаев, событий, испытуемых, образцов, и т.п.), некоторым способом выбранных из множества всех возможных прецедентов, называемого генеральной совокупностью.
Если исследователь не имеет возможности управлять выбором прецедентов, то обычно предполагается, что выбор прецедентов случаен. Если же выбором прецедентов можно управлять, то возникают задачи оптимального формирования выборки, см. также активное обучение, планирование экспериментов, выборочное обследование.
По каждому прецеденту собираются (измеряются) некоторые данные (data), образующие описание прецедента. Совокупность описаний всех прецедентов выборки является входной информацией для статистического анализа данных, интеллектуального анализа данных, машинного обучения.
Термины выборка (sample, set) и данные (data) взаимозаменяемы; иногда они употребляются вместе как один термин выборка данных (data set). Поэтому анализ данных можно понимать также как анализ конечных выборок. Основные цели анализа данных:
- проверка гипотез относительно имеющейся выборки данных;
- эмпирическая индукция — выявление общих закономерностей, присущих всей генеральной совокупности, по имеющийся выборке данных;
- прогнозирование — формирование статистически обоснованных предсказаний относительно новых данных, которые ещё не наблюдались.
Вероятностная модель порождения данных
Случайная выборка
Вероятностная модель порождения данных предполагает, что выборка из генеральной совокупности формируется случайным образом. Объём (длина) выборки считается произвольной, но фиксированной, неслучайной величиной.
Формально это означает, что с генеральной совокупностью связывается вероятностное пространство , где — множество всех выборок длины , — заданная на этом множестве сигма-алгебра событий, — вероятностная мера, как правило, неизвестная.
Случайная выборка — это последовательность из прецедентов, выбранная из множества согласно вероятностной мере .
Однородная выборка
Выборка называется однородной, если все её прецеденты одинаково распределёны, то есть выбраны из одного и того же распределения .
Независимая выборка
Выборка называется независимой, если вероятностная мера на представима в виде произведения вероятностных мер на , то есть для любой системы подмножеств
Если на существует плотность распределения , то независимость означает, что -мерная плотность распределения на представима в виде произведения одномерных плотностей:
Простая выборка
Простая выборка — это случайная, однородная, независимая выборка (i.i.d. — independent, identically distributed).
Эквивалентное определение: выборка простая, если значения являются реализациями независимых одинаково распределённых случайных величин.
Простая выборка является математической моделью серии независимых опытов. На гипотезу простой выборки существенно опираются многие методы статистического анализа данных и машинного обучения, в частности, большинство статистических тестов, а также оценки обобщающей способности в теории вычислительного обучения.
Также существует множество методов, не предполагающих однородность и/или независимость выборки, в частности, в теории случайных процессов, в прогнозировании временных рядов. Метод максимума правдоподобия позволяет оценивать значения параметров модели по обучающей выборке, в общем случае не требуя, чтобы выборка была однородной и независимой. Однако в случае простых выборок применение метода существенно упрощается.
Обучающая и тестовая выборка
Обучающая выборка (training sample) — выборка, по которой производится настройка (оптимизация параметров) модели зависимости.
Если модель зависимости построена по обучающей выборке , то оценка качества этой модели, сделанная по той же выборке оказывается, как правило, оптимистически смещённой. Это нежелательное явление называют переобучением. На практике оно встречается очень часто. Хорошую эмпирическую оценку качества построенной модели даёт её проверка на независимых данных, которые не использовались для обучения.
Тестовая (или контрольная) выборка (test sample) — выборка, по которой оценивается качество построенной модели. Если обучающая и тестовая выборки независимы, то оценка, сделанная по тестовой выборке, является несмещённой.
Оценку качества, сделанную по тестовой выборке, можно применить для выбора наилучшей модели. Однако тогда она снова окажется оптимистически смещённой. Для получения немсещённой оценки выбранной модели приходится выделять третью выборку.
Проверочная выборка (validation sample) — выборка, по которой осуществляется выбор наилучшей модели из множества моделей, построенных по обучающей выборке.
Источник
Что значит однородность выборки
Часть 3. Методы прикладной статистики
3.1.2. Методы проверки однородности характеристик двух независимых выборок
В прикладных исследованиях часто возникает необходимость выяснить, различаются ли генеральные совокупности, из которых взяты две независимые выборки. Например, надо выяснить, влияет ли способ упаковки подшипников на их потребительские качества через год после хранения. Или: отличается ли потребительское поведение мужчин и женщин. Если отличается – рекламные ролики и плакаты надо делать отдельно для мужчин и отдельно для женщин. Если нет – рекламная кампания может быть единой.
В математико-статистических терминах постановка задачи такова: имеются две выборки x1, x2. xm и y1, y2. yn (т. е. наборы из m и п действительных чисел), требуется проверить их однородность. Термин «однородность» уточняется ниже.
Противоположным понятием является «различие». Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если различия нет, то для дальнейшего изучения две рассматриваемые выборки часто объединяют в одну.
Например, в маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок, то возможно объединение сегментов, из которых они взяты, в один. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.
Традиционный метод проверки однородности (критерий Стьюдента). Для дальнейшего критического разбора опишем традиционный статистический метод проверки однородности. Вычисляют выборочные средние арифметические в каждой выборке
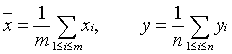
затем выборочные дисперсии
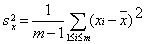
и статистику Стьюдента t, на основе которой принимают решение,
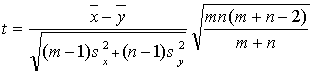
По заданному уровню значимости a и числу степеней свободы (m+n _ 2) из таблиц распределения Стьюдента находят критическое значение tкр. Если |t|>tкр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t| tкр проверяют, что t>tкр; эту постановку рассматривать не будем, так как в ней нет принципиальных отличий от обсуждаемой здесь.)
Рассмотрим условия применимости традиционного метода проверки однородности, основанного на использовании статистики t Стьюдента, а также укажем более современные методы.
Вероятностная модель порождения данных. Для обоснованного применения эконометрических методов необходимо прежде всего построить и обосновать вероятностную модель порождения данных. При проверке однородности двух выборок общепринята модель, в которой x1, x2. xm рассматриваются как результаты m независимых наблюдений некоторой случайной величины Х с функцией распределения F(x), неизвестной статистику, а y1, y2. yn — как результаты п независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Предполагается также, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.
Возможность применения модели в конкретной реальной ситуации требует обоснования. Независимость и одинаковая распределенность результатов наблюдений, входящих в выборку, могут быть установлены или исходя из методики проведения конкретных наблюдений, или путем проверки статистических гипотез независимости и одинаковой распределенности с помощью соответствующих критериев [1].
Если проведено (т+п) измерений объемов продаж в (т+п) торговых точках, то описанную выше модель, как правило, можно применять. Если же, например, xi и yi — объемы продаж одного и того же товара до и после определенного рекламного воздействия, то рассматриваемую модель применять нельзя. В последнем случае используют модель связанных выборок. В ней обычно строят новую выборку zi = xi — yi и используют статистические методы анализа одной выборки, а не двух. Методы проверка однородности для связанных выборок рассматривается в разделе 3.1.6.
При дальнейшем изложении принимаем описанную выше вероятностную модель двух выборок.
Уточнения понятия однородности. Понятие «однородность», т. е. «отсутствие различия», может быть формализовано в терминах вероятностной модели различными способами.
Наивысшая степень однородности достигается, если обе выборки взяты из одной и той же генеральной совокупности, т. е. справедлива нулевая гипотеза
Отсутствие однородности означает, что верна альтернативная гипотеза, согласно которой
хотя бы при одном значении аргумента x0. Если гипотеза H0 принята, то выборки можно объединить в одну, если нет — то нельзя.
В некоторых случаях целесообразно проверять не совпадение функций распределения, а совпадение некоторых характеристик случайных величин Х и Y — математических ожиданий, медиан, дисперсий, коэффициентов вариации и др. Например, однородность математических ожиданий означает, что справедлива гипотеза
где M(Х) и M(Y) — математические ожидания случайных величин Х и Y, результаты наблюдений над которыми составляют первую и вторую выборки соответственно. Доказательство различия между выборками в рассматриваемом случае — это доказательство справедливости альтернативной гипотезы
Если гипотеза H0 верна, то и гипотеза H’0 верна, но из справедливости H’0 , вообще говоря, не следует справедливость H0. Математические ожидания могут совпадать для различающихся между собой функций распределения. В частности, если в результате обработки выборочных данных принята гипотеза H’0, то отсюда не следует, что две выборки можно объединить в одну. Однако в ряде ситуаций целесообразна проверка именно гипотезы H’0 . Например, пусть функция спроса на определенный товар или услугу оценивается путем опроса потребителей (первая выборка) или с помощью данных о продажах (вторая выборка). Тогда маркетологу важно проверить гипотезу об отсутствии систематических расхождений результатов этих двух методов, т.е. гипотезу о равенстве математических ожиданий. Другой пример – из производственного менеджмента. Пусть изучается эффективность управления бригадами рабочих на предприятии с помощью двух организационных схем, результаты наблюдения — объем производства на одного члена бригады, а показатель эффективности организационной схемы — средний (по предприятию) объем производства на одного рабочего. Тогда для сравнения эффективности препаратов достаточно проверить гипотезу H’0 .
Классические условия применимости критерия Стьюдента. Согласно математико-статистической теории должны быть выполнены два классических условия применимости критерия Стьюдента, основанного на использовании статистики t, заданной формулой (1):
а) результаты наблюдений имеют нормальные распределения:
с математическими ожиданиями m1 и m2 и дисперсиями s1 2 и s2 2 в первой и во второй выборках соответственно;
б) дисперсии результатов наблюдений в первой и второй выборках совпадают:
Если условия а) и б) выполнены, то нормальные распределения F(x) и G(x) отличаются только математическими ожиданиями, а поэтому обе гипотезы H0 и H’0 сводятся к гипотезе
а обе альтернативные гипотезы H1 и H’1 сводятся к гипотезе
Если условия а) и б) выполнены, то статистика t при справедливости H»0 имеет распределение Стьюдента с (т + п — 2) степенями свободы. Только в этом случае описанный выше традиционный метод обоснован безупречно. Если хотя бы одно из условий а) и б) не выполнено, то нет никаких оснований считать, что статистика t имеет распределение Стьюдента, поэтому применение традиционного метода, строго говоря, не обосновано. Обсудим возможность проверки этих условий и последствия их нарушений.
Имеют ли результаты наблюдений нормальное распределение? Как показано в главе 2.1, априори нет оснований предполагать нормальность распределения результатов экономических, технико-экономических, технических, медицинских и иных наблюдений. Следовательно, нормальность надо проверять. Разработано много статистических критериев для проверки нормальности распределения результатов наблюдений [1]. Однако проверка нормальности — более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистики t Стьюдента, так и с использованием непараметрических критериев, рассматриваемых ниже).
Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. В главе 2.1 показано, что для того, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений. В большинстве технических, экономических, медицинских и иных исследований число наблюдений существенно меньше.
Как уже отмечалось, есть и одна общая причина отклонений от нормальности: любой результат наблюдения записывается конечным (обычно 2-5) количеством цифр, а с математической точки зрения вероятность такого события равна 0. Следовательно, в прикладной статистике распределение результатов наблюдений практически всегда более или менее отличается от нормального распределения.
Последствия нарушения условия нормальности. Если условие а) не выполнено, то распределение статистики t не является распределением Стьюдента. Однако при справедливости H’0 и условии б) распределение статистики t при росте объемов выборок приближается к стандартному нормальному распределению Ф(х)=N(x; 0, 1). К этому же распределению приближается распределение Стьюдента при возрастании числа степеней свободы. Другими словами, несмотря на нарушение условия нормальности традиционный метод (критерий Стьюдента) можно использовать для проверки гипотезы H’0 при больших объемах выборок. При этом вместо таблиц распределения Стьюдента достаточно пользоваться таблицами стандартного нормального распределения Ф(х).
Сформулированное в предыдущем абзаце утверждение справедливо для любых функций распределения F(x) и G(x) таких, что M(X)=M(Y), D(X)=D(Y) и выполнены некоторые внутриматематические условия, обычно считающиеся справедливыми в реальных задачах. Если же M(X)¹M(Y), то нетрудно вычислить, что при больших объемах выборок
P(t 2 в (1) стоит множитель (m — 1), а в (6)- множитель п.
Если M(X)¹M(Y), то при больших объемах выборок
P(T 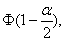
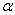
В прикладной статистике наиболее часто применяется уровень значимости 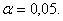
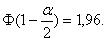
Из сказанного выше следует, что применение критерия Крамера-Уэлча не менее обосновано, чем применение критерия Стьюдента. Дополнительное преимущество — не требуется равенства дисперсий D(X)=D(Y). Распределение статистики Т не является распределением Стьюдента, однако и распределение статистики t, как показано выше, не является таковым в реальных ситуациях.
Распределение статистики Т при объемах выборок т=п=6, 8, 10, 12 и различных функциях распределений выборок F(x) и G(x) изучено нами совместно с Ю.Э. Камнем и Я.Э. Камнем методом статистических испытаний (Монте-Карло). Рассмотрены различные варианты функций распределения F(x) и G(x). Результаты показывают, что даже при таких небольших объемах выборок точность аппроксимации предельным стандартным нормальным распределением вполне удовлетворительна. Поэтому представляется целесообразным во всех тех случаях, когда в настоящее время используется критерий Стьюдента, заменить его на критерий Крамера-Уэлча. Конечно, такая замена потребует переделки ряда нормативно-технических и методических документов, исправления учебников и учебных пособий для вузов.
Пример 1. Пусть объем первой выборки 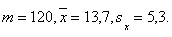
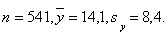
Поскольку полученное значение по абсолютной величине меньше 1,96, то гипотеза однородности математических ожиданий принимается на уровне значимости 0,05.
Непараметрические методы проверки однородности. В большинстве технических, экономических, медицинских и иных задач представляет интерес не проверка равенства математических ожиданий или иных характеристик распределения, а обнаружение различия генеральных совокупностей, из которых извлечены выборки, т.е. проверка гипотезы H0. Методы проверки гипотезы H0 позволяют обнаружить не только изменение математического ожидания, но и любые иные изменения функции распределения результатов наблюдений при переходе от одной выборки к другой (увеличение разброса, появление асимметрии и т. д.). Как установлено выше, методы, основанные на использовании статистик t Стьюдента и Т Крамера-Уэлча, не позволяют проверять гипотезу H0 . Априорное предположение о принадлежности функций распределения F(x) и G(x) к какому-либо определенному параметрическому семейству (например, семействам нормальных, логарифмически нормальных, распределений Вейбулла-Гнеденко, гамма-распределений и др.), как также показано выше, обычно нельзя достаточно надежно обосновать. Поэтому для проверки H0 следует использовать методы, пригодные при любом виде F(x) и G(x), т.е. непараметрические методы. (Напомним, что термин «непараметрический метод» означает, что при использовании этого метода нет необходимости предполагать, что функции распределения результатов наблюдений принадлежат какому-либо определенному параметрическому семейству.)
Для проверки гипотезы H0 разработано много непараметрических методов — критерии Смирнова, типа омега-квадрат (Лемана — Розенблатта), Вилкоксона (Манна-Уитни), Ван-дер-Вардена, Сэвиджа, хи-квадрат и др. [1, 2, 7]. Распределения статистик всех этих критериев при справедливости H0 не зависят от конкретного вида совпадающих функций распределения F(x)ºG(x). Следовательно, таблицами точных и предельных (при больших объемах выборок) распределений статистик этих критериев и их процентных точек [1, 2] можно пользоваться при любых непрерывных функциях распределения результатов наблюдений.
Каким из непараметрических критериев пользоваться? Как известно [3], для выбора одного из нескольких критериев необходимо сравнить их мощности, определяемые видом альтернативных гипотез. Сравнению мощностей критериев посвящена обширная литература.
Хорошо изучены свойства критериев при альтернативной гипотезе сдвига
Критерии Вилкоксона, Ван-дер-Вардена и ряд других ориентированы для применения именно в этой ситуации. Если m раз измеряют характеристику одного объекта и п раз — другого, а функция распределения погрешностей измерения произвольна, но не меняется при переходе от объекта к объекту (это более жесткое требование, чем условие равенства дисперсий), то рассмотрение гипотезы H1c оправдано. Однако в большинстве технических, экономических, медицинских и иных исследований нет оснований считать, что функции распределения, соответствующие выборкам, различаются только сдвигом.
Источник