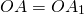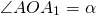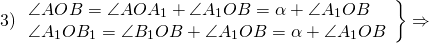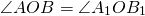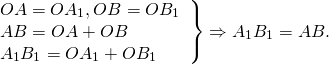Что значит один поворот

Водитель моргает то левым, то правым поворотником — что это значит?

\

Язык водителей на дороге полон секретных знаков, которые новички порой просто не понимают и ломают голову, что же хотел сказать коллега. Эту азбуку не преподают в автошколе, хотя ее стоит знать каждому. О самых часто используемых знаках знают все, уже не нужно объяснять, что такое моргнуть аварийкой или дальним светом. А вот что значит, если водитель, который едет впереди вас, начинает моргать то левым, то правым поворотником?

Один водитель рассказал на форуме об очень необычном использовании сигналов в качестве средства для общения. Он ехал по трассе, пошел на обгон фуры, закончил успешно манёвр и вернулся в свой ряд. И вдруг нашего героя обгоняет легковушка и начинает моргать поворотниками, то левым, то правым.

Знаете, что это значит? Это жест поучения — дескать, водитель, когда пошел на обгон, забыл включить поворотник и мог ввести в заблуждение других участников дорожного движения. Как оказалось, такой сигнал является традиционным на дороге, но водители его используют нечасто, только чтобы поучить уму-разуму других автомобилистов. Чаще всего такой жест можно встретить на трассе.

Сами понимаете, что не включенный поворотник может спровоцировать аварию, особенно на трассе, когда машины едут с достаточно большой скоростью, и на экстренный манёвр гораздо меньше времени, чем в загруженных городских условиях, где машинам негде разогнаться до трассовых скоростей.

Поэтому не забывайте ПДД и включайте сигналы заблаговременно до совершения маневра, думайте не только о себе и за себя, но и о других и за того парня. Не провоцируйте других водителей на резкие действия, не создавайте аварийных ситуаций на пустом месте.

Источник

Угол поворота, угол произвольной величины

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

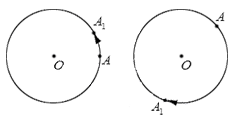
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Полный оборот

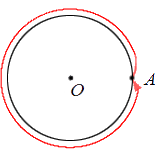
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

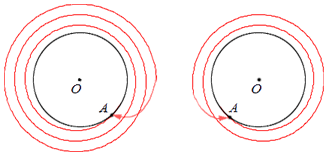
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

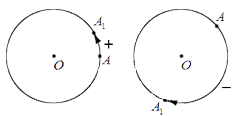
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

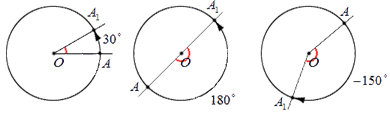
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

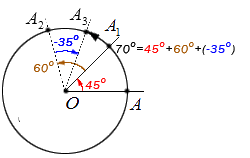
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

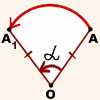
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Источник

Значение слова «поворот»

1. Действие по знач. глаг. поворотить—повернуть—поворачивать; действие и состояние по знач. глаг. поворотиться—повернуться—поворачиваться. Катер делает широкий поворот в Морской канал. Вишневский, Мы из Кронштадта. Лицо мужчины, закуривающего сигарету, снято крупно, в трехчетвертном повороте. Прибытков, Завещаю вам жизнь. || Разг. То же, что оборот (в 1 знач.). Медленно земля совершала свой поворот и, казалось, уходила от солнца навстречу ночи. Арсеньев, По Уссурийской тайге. Оставшись один, Бражников на два поворота ключа запирает дверь. Ленч, Мимолетное видение.

2. Место, где дорога поворачивает, отклоняется в сторону. Встретиться на повороте дороги. □ — Куда? — сказал извозчик. — Пошел прямо! — Как прямо? тут поворот: направо или налево? Гоголь, Нос. Извозчик подвез Нехлюдова не к самой тюрьме, а к повороту, ведущему к тюрьме. Л. Толстой, Воскресение.

3. перен. Полное изменение в развитии чего-л.; перелом. Грустно и тяжко думал [Нежданов] о предстоящей ему поездке, об этом новом, неожиданном повороте его судьбы. Тургенев, Новь. Лидочке было двенадцать лет, когда в ее жизни совершился решительный поворот. Салтыков-Щедрин, Мелочи жизни.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Поворо́т (враще́ние) — движение, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной.

Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства). Часто под термином вращение понимают собственное вращение.

Для двумерной плоскости можно дать другое, эквивалентное, определение вращения: вращение плоскости это движение, при котором каждый луч, исходящий из данной точки поворачивается на один и тот же угол в одном и том же направлении.

В физике (механике) нередко поворотом называется неполное вращение, или, наоборот, вращение рассматривается как частный вид поворота. Последнее определение более строго, поскольку понятие поворот охватывает значительно более широкую категорию движений, в том числе и такое, при котором траектория движущегося тела в избранной системе отсчёта представляет собой незамкнутую кривую.

ПОВОРО’Т, а, м. 1. Действие и состояние по глаг. поворотить-поворачивать и поворотиться-поворачиваться. П. кругом. Ловкий п. 2. Место, где что-н. поворачивает, отклоняется в сторону. На повороте дороги. Полегче на поворотах. || Место, где поворачивали, след. От ворот поворот виден по́ снегу. А. Кольцов. 3. перен. Полное изменение в направлении, в развитии чего-н., перелом. . Коренной поворот деревни к социализму можно считать уже обеспеченным. Сталин (1930 г.). В деле произошел п. П. дела в нашу пользу. П. в настроениях. ◊

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

поворо́т

1. действие по значению гл. поворачивать; изменение направления чего-либо

2. место изменения направления (дороги, пути, линии и т. п.)

Источник

Поворот

Отметим на плоскости точку O — центр поворота. Зададим угол α — угол поворота.

Поворот плоскости вокруг точки O на угол α — это отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, что

При этом точка O остаётся на месте (отображается сама в себя), а все остальные точки поворачиваются вокруг точки O в одном и том же направлении — либо по часовой стрелке, либо против часовой стрелки.

Поворот является движением

(то есть отображением плоскости на себя, сохраняющим расстояние).

Если точки A, O и B не лежат на одной прямой.

Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.

Проведём отрезки AB и A1B1.

Рассмотрим треугольники AOB и A1OB1.

2) OB=OB1 (по определению поворота).

Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.

Если точки A, O и B лежат на одной прямой.

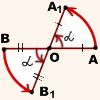
При повороте в направлении по часовой стрелке все рассуждения аналогичны.

Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.

Источник