Функция
|
1. Понятие функцииПонятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. 2. Cвойства функций1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида. 2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1 ) x2, f(x1) ) f(x2). 3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической. 4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | 0 a≠1) область определения (-∞,∞) Логарифмическая функция у = log ₐ x (a>0 a≠1) область определения (0,∞) Тригонометрические функции y = sin x область определения (-∞; ∞) y = cos x область определения (-∞; ∞) y = tg x область определения y = ctg x область определения y = arcsin x область определения [-1; 1] y = arccos x область определения [-1; 1] y = arctg x область определения (-∞; ∞) y = arcctg x область определения (-∞; ∞) Источник Глава 39. Понятие функции. Основные свойства функцийПостоянной величиной называется величина, сохраняющая одно и тоже значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная p. Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется Параметром. Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении S = vt, где путь S и время t – переменные величины, а v – параметр. Если каждому элементу При этом Множество Например, область определения функции Способы задания функций Задать функцию – значит Указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие значение функции из области значений функций. Существует три основных способа задания функций: Табличный, аналитический и графический. Табличный способ Состоит в том, что функция задается таблицей, содержащей значения аргумента Аналитический способ состоит в задании связи Имеет два аналитических выражения, используемых при различных значениях аргумента. Графический способ Состоит в том, что соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях и употреблением самопишущих приборов (осциллографы, сейсмографы и т. д.). Основные свойства функции 1. Четность и нечетность. Функция Например, функция График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. Функция Пусть Функции возрастающие и убывающие называются Монотонными функциями. Так, например, функция Функция Например, функция Функция Например, функция Источник | ||||||||||||



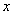 множества
множества  (
(  ) ставится в соответствие вполне определенный элемент
) ставится в соответствие вполне определенный элемент  множества
множества  (
(  ), то говорят, что на множестве
), то говорят, что на множестве  .
. обозначает закон соответствия.
обозначает закон соответствия. есть полуинтервал
есть полуинтервал  , так как
, так как  ; если же переменная
; если же переменная  областью определения функции будет отрезок
областью определения функции будет отрезок  .
.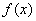 , например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т. п.
, например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т. п.
 И Нечетной, Если
И Нечетной, Если  . В противном случае функция
. В противном случае функция  является четной, а функция
является четной, а функция  – нечетной. Функция
– нечетной. Функция  является функцией общего вида, так как
является функцией общего вида, так как  и
и  И
И  .
. и
и  . Тогда функция возрастает на промежутке X, если
. Тогда функция возрастает на промежутке X, если  и убывает, если
и убывает, если  .
. убывает и при
убывает и при  – возрастает.
– возрастает. Для любого
Для любого  ограничена на всей числовой оси, так как
ограничена на всей числовой оси, так как  для любого
для любого  .
. , если для любых X из области определения функции
, если для любых X из области определения функции  .
. , так как для любых
, так как для любых  .
.

