общее высказывание
Большой англо-русский и русско-английский словарь . 2001 .
Смотреть что такое «общее высказывание» в других словарях:
Высказывание — общее значение – единица речи или разговора, в котором выражается определённая мысль.Это может быть междометие, то есть простой вокальный звук (например, «ах»), и обширный, составленный из многих предложений дискурс (лат. discursus – рассуждение) … Энциклопедический словарь по психологии и педагогике
Высказывание (лингвистика) — У этого термина существуют и другие значения, см. Высказывание. Высказывание речевое произведение, созданное в ходе конкретного речевого акта. Рассматривается в контексте этого речевого акта как часть дискурса (текста). Содержание 1… … Википедия
Высказывание — Высказывание единица речевого общения. Потребность в выделении высказывания как лингвистического понятия связана с углублением исследования функционирования языковых форм в речи. Высказывание определяется по отношению к понятию предложения.… … Лингвистический энциклопедический словарь
ВЫСКАЗЫВАНИЕ — Очень общее значение – единица речи или разговора. Высказыванием может быть все, что угодно, от одного простого вокального звука ( ах ) до обширного, состоящего из многих предложений дискурса. Точное определение того, где начинается и… … Толковый словарь по психологии
ОПИСАНИЕ — ОПИСАНИЕ, дескрипция (англ. description описание) 1) процедуры фиксации средствами естественного или искусственного языка сведений об объектах, фиксируемых в наблюдении, эксперименте и измерении; 2) способ языковой индивидуализации объектов,… … Новейший философский словарь
БЕСКОНЕЧНАЯ ИНДУКЦИЯ — тот крайний вид индуктивного умозаключения, когда общее высказывание (суждение, положение) получается как заключение из бесконечной совокупности посылок, исчерпывающих все частные случаи. Пример Б. и.: 1 + 0 = 0 + 1; 1 + 1 = 1 + 1; 1 +2 = 2 + 1;… … Философская энциклопедия
ОПИСАНИЕ, дескрипция — (англ. description описание) 1) процедуры фиксации средствами естественного или искусственного языка сведений об объектах, фиксируемых в наблюдении, эксперименте и измерении; 2) способ языковой индивидуализации объектов, позволяющий осмысливать… … Социология: Энциклопедия
ПРИНЦИП — нормативное общее высказывание, содержащее определенное требование к осуществлению познавательной, практической и духовной деятельности (принцип относительности, принцип соответствия, принцип эффективности, моральные заповеди и т. п.). (См.… … Философия науки: Словарь основных терминов
КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия
понятие — общее имя, имеющее относительно ясное и устойчивое содержание и сравнительно четко очерченный объем. П. являются, напр., дом , квадрат , молекула , кислород , атом , любовь , бесконечный ряд и т. п. Отчетливой границы между теми именами, которые… … Словарь терминов логики
УНИВЕРСАЛИИ — (от лат. universalis общий) общие понятия. В филос. проблеме онтологического и гносеологического статуса У. ставится вопрос о том, что такое реальное бытие, каким образом существует идеальное, как возможно рациональное понятийное познание, как… … Философская энциклопедия
Источник
Пять уроков по логике
Описание разработки
Содержание:
- Основы логики
- Логические операции
- Логические схемы
- Импликация и эквивалентность
- Формулы сокращения
- Задачник-логика
- Задание логическая схема
- Задание таблица истинности
- Основы логики теория
Все задания можно выдавать в распечатанном виде.
Тема Логическая информация и основы логики.
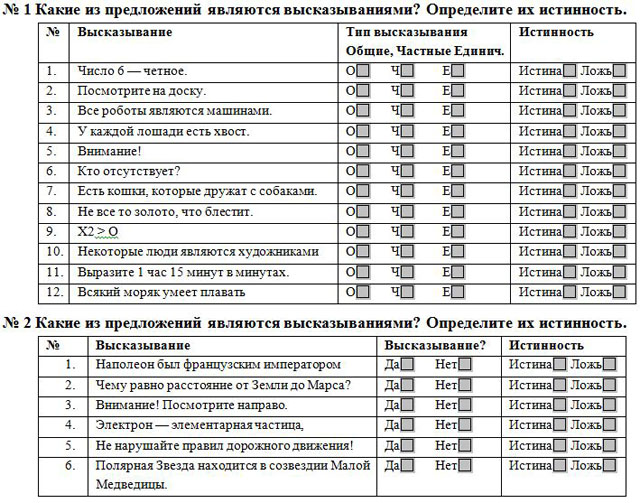
Высказывание (суждение) — предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно.
Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается (или можно начать) со слов: некоторые, большинство и т. п. Во всех других случаях высказывание является единичным.
Пример 1. Определить значения истинности для следующих высказываний
«Лед — твердое состояние воды ». Ответ: истинное высказывание
«Треугольник — это геометрическая фигура». Ответ: истинное высказывание
«Париж — столица Китая» Ответ: ложное высказывание
Пример 2. Определить тип высказывания (общее, частное, единичное)
«Все рыбы умеют плавать». Ответ: общее высказывание
«Некоторые медведи — бурые». Ответ: частное высказывание.
«Буква А — гласная». Ответ: единичное высказывание.
№ 3 Какие из приведенных высказываний являются общими? (поставьте крестик)
- Не все книги содержат полезную информацию
- Кошка является домашним животным
- Все солдаты храбрые
- Ни один внимательный человек не совершит оплошность
- Некоторые ученики двоечники
- Все ананасы приятны на вкус
- Мой кот страшный забияка
- Любой неразумный человек ходит на руках-
№ 4 Какие из приведенных высказывании являются частными? (поставьте крестик)
- Некоторые мои друзья собирают марки,
- Все лекарства неприятны на вкус,
- Некоторые лекарства приятны на вкус. 4- А — первая буква в алфавите.
- Некоторые медведи — бурые.
- Тигр — хищное животное.
- У некоторых змей нет ядовитых зубов.
- Многие растения обладают целебными свойствами.
- Все металлы проводят тепло,
Источник
Высказывания
Речь человека, тексты, которые он читает и пишет, состоят из предложений. Это касается и обычного, и математического языка.
То, что говориться в каждом предложении, может оказаться верным или неверным.
В учебнике можно прочитать верное предложение„ Земля вращается вокруг Солнца”, а в таблице умножения — предложение 2×2=4. А если ученик скажет, что 7×7=47 – это будет неверное предложение. Надо сказать, что и в учебниках встречаются неверные предложения – из — за отпечаток, а иногда и по невнимательности.
Верные и неверные предложения называют в математике высказываниями или утверждениями.
При этом вместо слов “ верное ” и „неверное” часто говорят истинное и ложное. Таким образом, утверждения бывают истинные и ложные
В высказываниях всегда можно выделить тему – то, о чем говорится, и рему – то, что сообщается о теме. Например, в написанном выше предложении говорится о планете Земля – это тема, и сообщается, что она вращается вокруг Солнца – это рема. Точно так же в математическом предложении 28+36=64 говорится о сумме чисел 28 и 36 и сообщается, что эта сумма равна 64.
Не всякое предложение является утверждением. В самом деле, если кто-нибудь спрашивает„ Который час?” или кричит„ Ура!” не имеет никакого смысла говорить о том, верны или неверны эти предложения. В первом из этих предложений тема есть, а ремы нет, а во втором нет даже темы. В данной работе я пробовала обобщить интересный материал по теме высказывания.
— рассмотреть виды высказываний
— сравнить доказательство разных типов высказываний
— составить задачи и их решить.
Виды высказываний
Высказывание, называется общим потому-то все элементы некоторого множества, обладают определенным свойством.
Высказывание, в котором утверждается о том, что в заданном множестве существует хотя бы один элемент, обладающий определенным свойством, называется
Определить вид высказывание помогает не все предложение, а ключевые слова, которые используются при его составлении. Например, высказывание: Каждый класс имеет компьютер. Ключевое слово» Каждый» помогает понять, что речь в предложении идет обо всех классах. Значит высказывание общее.
Например, высказывание: Иногда класс не имеет компьютер. Ключевое слово» Иногда » помогает понять, что речь в предложении идет не обо всех классах, а о тех классах, в которых нет компьютера. Значит, существует хотя бы один класс, в котором нет компьютера. Данное высказывание о существовании.
Чтобы облегчить определение вида высказывания, я собрала все выше сказанное в памятку в виде таблицы с примерами.
Вид Общее О существовании
Ключевые слова Все, каждый, всегда, любой. Иногда, существует, хотя бы один, некоторые, есть.
Примеры 1) Произведение любых двух натуральных чисел больше их Существует такое натуральное число х, что суммы. ( 2х + 3 ) : 7 = 11.
2) Все натуральные числа больше единицы. Иногда шторм длится более 5 дней.
3) В каждом месяце не меньше 30 дней. 4) Сумма двух Хотя бы один человек имеет домашнее животное.
натуральных чисел всегда делится на 3. Некоторые люди носят очки.
Есть люди, которые не умеют плавать.
Истинность
Вместо слов “верное” и “неверное” часто говорят истинное и ложное. Таким образом, утверждения бывают истинные и ложные.
Все дети любят молоко. (л. )
Существует ребенок который не любит молоко. (и. )
Истинность или ложность буквенных выражений зависит от значения переменной.
12х-35у=1 (х=3, у=1) (и. )
12х-35у=1 (х=4, у=2) (л. )
Доказательство
Все элементы некоторого множества обладают определенным свойством.
В общих высказываниях говориться о том, что все элементы множества обладают данным свойством.
Значит, чтобы доказать истинность общих высказываний надо проверить по очереди все элементы множества.
Но, если множество бесконечное, то возникает математическая проблема.
В высказываниях о существовании говориться, о том, что некоторые элементы множества обладают данным свойством.
Значит, чтобы доказать истинность высказываний о существовании надо найти хотя бы один элемент множества с данным свойством.
(Привести пример, доказывающий высказывание).
Чтобы облегчить выбор способа доказательства , я собрала все выше сказанное в памятку в виде таблицы с примерами.
Общее О существовании
Проверить по очереди все элементы множества, Привести пример, доказывающий высказывание.
1. 12+17=29 1. 2х-4=92
Что бы проверить истинность надо выполнить действие 12+17=29 значит Что бы доказать истинность надо решить уравнение высказывание истинное. 2х-4=92
2. Все числа делятся на 1. 2х=92+4
Это верно для любого числа а. Х=96:2
3. Числа 5, 3, 2 являются делителем числа 300 чтобы доказать истинность надо Х=48
выполнить деление 300:5=60, 300:3=100, 300:2=150. Уравнение имеет решение, значит высказывание истинное.
2. Бывают железные коты.
Это высказывание истинное, потому что в Казане на улице Баумана построен памятник кота Екатерины II.
Авторские задачи
1. Все дети любят слушать музыку.
2. Некоторые люди не работают.
3. Существует человек, который любит играть на гитаре.
1. Все дети любят слушать музыку. ( Л. )
2. Некоторые люди не работают. (И. )
3. Существует человек, который любит играть на гитаре. (И. )
1. Все натуральные числа больше нуля.
3. Существует число Х, для которого верно: 72:х=9.
1. Все натуральные числа больше нуля. (И. )
3. Существует число Х, для которого верно: 72:х=9. (И. )
Определить истинность при данных значениях переменных.
Источник
Общие фразы
Фразеологический словарь русского литературного языка. — М.: Астрель, АСТ . А. И. Фёдоров . 2008 .
Смотреть что такое «Общие фразы» в других словарях:
ГОСТ 24867-81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению — Терминология ГОСТ 24867 81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению оригинал документа: 4.4. Брошюровка, переплет 4.4.1. В зависимости от общего объема… … Словарь-справочник терминов нормативно-технической документации
фраза — ы; ж. [от греч. phrasis выражение, оборот речи] 1. Отрезок речи, относительно самостоятельный в смысловом и интонационном отношении (обычно сопровождается паузой). Чёткие, запутанные фразы. Неполная ф. (выражающая недоговорённую мысль). Грамотно… … Энциклопедический словарь
фраза — ы; ж. (от греч. phrasis выражение, оборот речи) см. тж. фразовый 1) Отрезок речи, относительно самостоятельный в смысловом и интонационном отношении (обычно сопровождается паузой) Чёткие, запутанные фразы. Неполная фра/за. (выражающая… … Словарь многих выражений
Арнаутский диалект — Арнаутский язык (Арванитка) Самоназвание: Arbёrisht Страны: Греция … Википедия
Птолемей IV Филопатор — В Википедии есть статьи о других людях с именем Птолемей. Птолемей IV Филопатор др. греч. Πτολεμαῖος Φιλοπάτωρ («Птолемей Любящий отца») … Википедия
ПОР-РОЯЛЯ ЛОГИКА — логич. учение, основанное на принципах философии Декарта и Паскаля. Систематически изложено в книге Арно и Николя Логика или искусство мыслить ( La logique ou l art de penser , P., 1662). Согласно П. Р. л., главная цель логики – формулировка… … Философская энциклопедия
Шухевич, Роман Иосифович — В Википедии есть статьи о других людях с такой фамилией, см. Шухевич. Роман Иосифович Шухевич укр. Роман Йосипович Шухевич … Википедия
Волынская резня — Эта статья находится в режиме поиска консенсуса. В настоящее время вокруг статьи происходит сложный конфликт участников, из за которого администраторы перевели её в особый режим. Существенные правки … Википедия
Роман Иосифович Шухевич — Роман Осипович Шухевич Роман Йосипович Шухевич Род деятельности: главнокомандующий Украинской повстанческой армией Дата рождения: 30 июня или 17 июля 1907 … Википедия
Роман Шухевич — Роман Осипович Шухевич Роман Йосипович Шухевич Род деятельности: главнокомандующий Украинской повстанческой армией Дата рождения: 30 июня или 17 июля 1907 … Википедия
Источник
Формы мышления
Формы мышления
Логика — это наука о формах и способах мышления. Первые учения о формах и способах рассуждений возникли в странах Древнего Востока. Основы формальной логики заложил Аристотель.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
По отношению друг к другу понятия делятся на сравнимые и не сравнимые (романс и кирпич, безответственность и нитка)
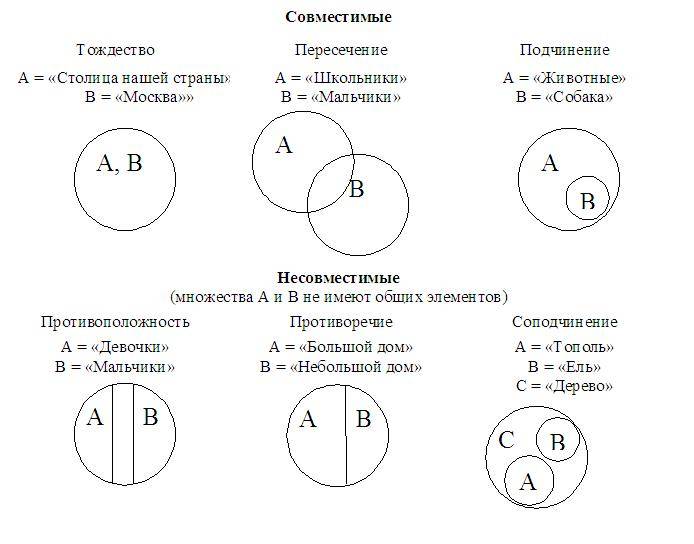
У сравнимых понятий бывают совместимыми или несовместимыми их объемы: (проиллюстрируем примеры с помощью кругов Эйлера–Венна)
Логическое высказывание (суждение) — это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать истиннo oнo или лoжнo.
Предложение «6 — четное число» истинное высказыванием
Предложение «Рим — столица Франции» ложное высказывание
Луна — спутник Земли» – истинное высказыванием.
Высказывания бывают общими, частными или единичными.
Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. «Все рыбы умеют плавать»— общее высказывание.
Частное высказывание начинается (или можно начать) со слов: некоторые, большинство, и т.п. «Некоторые медведи- бурые» — частное высказывание.
Во всех других случаях высказывание является единичным. «Буква А-гласная»- единичное высказывание.
Высказывания могут быть простыми и сложными.
Примеры простых высказываний: Лето очень жаркое. Снегири прилетели. Идет дождь.
Примеры сложных высказываний: Пришла весна, и появились подснежники. Если я хорошо сдам экзамены, то поступлю в институт.
Сложные высказывания строятся из простых с помощью логических связок (операций) «и», «или», «не», «если … то», «тогда и только тогда» и др. Высказывания обозначаются заглавными буквами А, В, С и т.д.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Пример: Все металлы – простые вещества. Литий – металл. Следовательно, литий – простое вещество.
Источник