Что значит обратная задача пример

Что означает обратная задача в математике?

Что такое обратная задача?

Начиная со второго класса, детям регулярно задают на дом задания. Большое внимание педагоги уделяют решению задач, ведь именно за них ребенок получает больше баллов на контрольных и тестах.

Понятие «обратная задача» знакомо всем ученикам школы, в которой учатся мои дети, даже тем, кто не любит математику и далек от нее.

По сути, обратная данной задача, — это задача в которой искомое и заданное поменялись местами. Для того чтобы решить ее, нужно для начала решить заданную.

В качестве примера рассмотрим задачу с решением в одно действие: На столе было 5 груш и 4 яблока, сколько фруктов было всего. Решение простое: 5+4=9.

В данном случае, можно составить и решить две задачи обратные данной:

• Всего на столе было 9 фруктов, из них 5 груш. Сколько было яблок?
• Всего на столе было 9 фруктов, из них 4 яблока. Сколько было груш?

Чем больше данных в задаче, тем больше обратных задач можно к ней составить.

Обратные задачи просты и понятны большинству учеников младших классов.

Если же ваш ребенок пропустил эту тему, не понимает, что от него требуется, научить его составлять обратные задачи не составит труда, так как данная тема легко воспринимается даже детьми с гуманитарным складом ума.

Достаточно интересна и познавательна для родителей тема: «Как помочь ребенку преодолеть школьные проблемы», рекомендую с ней, по желанию, ознакомиться.

Источник

Обратные задачи
учебно-методический материал по математике (1, 2 класс) на тему

Обратные задачи. Памятка к материалу по математике для 2 класса

Скачать:

Вложение	Размер
obratnye_zadachi.docx	27.56 КБ

Предварительный просмотр:

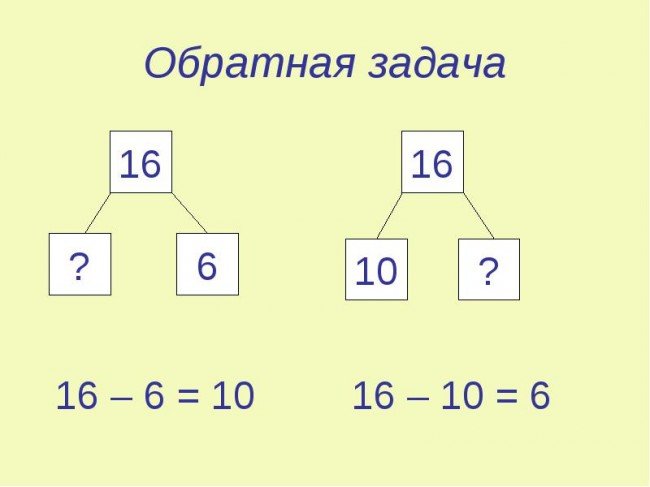
Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно.

Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок?

На тарелке – 6 ябл.

В корзине – 10 ябл. ? ябл.

Ответ: 16 яблок всего.

На тарелке – 6 ябл.

В корзине – ? ябл. 16 ябл.

Ответ: 10 яблок в корзине.

На тарелке – ? ябл.

В корзине – 10 ябл. 16 ябл.

Ответ: 6 яблок на тарелке.

Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно.

Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок?

На тарелке – 6 ябл.

В корзине – 10 ябл. ? ябл.

Ответ: 16 яблок всего.

На тарелке – 6 ябл.

В корзине – ? ябл. 16 ябл.

Ответ: 10 яблок в корзине.

На тарелке – ? ябл.

В корзине – 10 ябл. 16 ябл.

Ответ: 6 яблок на тарелке.

Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно.

Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок?

На тарелке – 6 ябл.

В корзине – 10 ябл. ? ябл.

Ответ: 16 яблок всего.

На тарелке – 6 ябл.

В корзине – ? ябл. 16 ябл.

Ответ: 10 яблок в корзине.

На тарелке – ? ябл.

В корзине – 10 ябл. 16 ябл.

Ответ: 6 яблок на тарелке.

Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно.

Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок?

На тарелке – 6 ябл.

В корзине – 10 ябл. ? ябл.

Ответ: 16 яблок всего.

На тарелке – 6 ябл.

В корзине – ? ябл. 16 ябл.

Ответ: 10 яблок в корзине.

На тарелке – ? ябл.

В корзине – 10 ябл. 16 ябл.

Ответ: 6 яблок на тарелке.

По теме: методические разработки, презентации и конспекты

откр.урок- обратные задачи 2класс.

откр.урок- обратные задачи 2класс.

Презентация к уроку «Обратная задача»

Презентация предназначена для иллюстрации нового маматериала.

Математика. 1 класс. Урок 60. Обратные задачи — Презентация

ссылка на источник: http://avtatuzova.ru/news/matematika_1_klass_urok_60_obratnye_zadachi/2012-12-20-153 Урок 60. Обратные задачи В презентации отображены: задан.

«ОБРАТНЫЕ ЗАДАЧИ»

урок по математике во 2 классе.

Обратные задачи

Урок математики по теме «Обратные задачи» 2 класс.

методическая разработка урока математики 2 класс(обратные задачи)

конспект урока по мамтематике «Школа России» 2 класс.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 10. Задачи, обратные данной

Перечень вопросов, рассматриваемых в теме:

1. Что такое задачи, обратные данной?
2. Как составлять и решать обратные задачи?

Глоссарий по теме:

Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27

2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17

3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31

Теоретический материал для самостоятельного изучения

Решим три задачи.

Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?

Составим схематический рисунок.

Ответ: 18 детей в классе.

Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Ответ: 8 мальчиков в классе.

Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?

Ответ: 10 девочек в классе.

Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.

Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.

Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.

1. Решите задачу. Выберите задачи, обратные данной.

Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?

1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?

2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?

3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?

1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?

3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?

2 . Восстановите пропуски в задачах.

1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?

2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?

3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?

30, 20, ясных, пасмурных, июне

1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?

2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?

3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?

Источник

Решение взаимно обратных задач в начальной школе (простые задачи)

ХОД УРОКА

1. Введение.

Перед нашей школой всегда стояла задача построения такой методической системы, которая обеспечивала бы резкое повышение качества знаний при значительной экономии времени, расходуемого на изучение материала. В наше время при все возрастающем потоке информации эта проблема стоит особенно остро.

Еще в 60-е годы Комиссией по определению содержания обучения математике, работающей в АПН СССР, был разработан проект программы по математике. Авторы проекта одним из главных средств ускоренного и сознательного изучения материала в школе считали изменение структуры существующих программ, осуществление более целесообразной группировки вопросов, рациональной группировки вопросов, рациональной последовательности разделов, то есть применение метода противопоставления на уроках математики.

Общепринятая традиционная система обучения математике соблюдает принцип раздельного изучения взаимосвязанных понятий или преобразований. При одновременном изучении взаимосвязанных вопросов в пределах одних и тех же уроков дидактической единицей усвоения становится более крупная единица знаний, чем в случае раздельного изучения их. Переход в обучении к более крупным дидактическим единицам усвоения знаний дает экономию сил и времени.

При изучении задач в курсе математики, как простых, так и сложных, как обычных арифметических, так и типовых оказывается высоко эффективным систематическое применение так называемого метода обратных задач.

Успех обучения решению задач посредством преобразования прямой задачи в обратные задачи объясняется как первопричиной тем, что такой путь заставляет поднимать из сферы подсознания наибольшее разнообразие связей, заключенных в содержании задачи. Это и обеспечивает – на языке дидактики – глубокое и прочное усвоение материала.

На составление и решение обратной задачи уходит несравненно меньше времени, чем на решение новой задачи, так как числовые данные и сюжет остаются прежними; производится здесь лишь логическая операция по переосмыслению ролей чисел; неизвестное в прямой задаче становится известным и наоборот.

Поэтому я взяла для изучения и последующей работы тему “Решение взаимно обратных задач в начальной школе”.

На мой взгляд, самое трудное в начальной школе – научить ребенка грамотно писать, а самое трудное в математике – научить решать задачи.

В процессе работы мне хотелось повысить процент способных детей и уменьшить процент слабых.

Кроме того, в своей работе я стремлюсь к тому, чтобы как можно больший процент детей имел качественный показатель знаний по математике. Далее я опишу, как я этого добиваюсь и каковы результаты молей работы.

Я ознакомилась с мнением различных ученых-методистов (смотреть список литературы) по вопросу классификации задач и решению взаимно обратных задач, как по традиционной, так и по развивающей методике.

Работа со взаимно обратными задачами просматривается у Аритской Н.И., у Свечникова А.А., но у Аритской И.И. нет четкой классификации задач, также, как у Истоминой Н.Б.

Классификация сложных задач в принципе сходна у Эрдниева П.М., Свечникова А.А., Баитовой М.А. но простые задачи Свечников А.А. и Баитова М.А. классифицируют несколько иначе, чем Эрдниев П.М.

За основу я взяла работу над задачами по Эрдниеву П.М., так как на сегодняшний день более четкой классификации задач и методики работы над взаимно обратными задачами я пока не вижу.

Следует отметить существенно важные дидактические достоинства метода обратных задач.

Во время преобразования задачи учащийся выявляет и использует взаимно обратные связи между величинами задачи:

Источник