- ПОНЯТИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ
- Обратная корреляция 2021
- Table of Contents:
- Что означает «обратная корреляция»
- РАЗРЕШЕНИЕ «Обратная корреляция»
- Пример расчета обратной корреляции
- Понятие корреляционной связи
- Корреляции в дипломных работах по психологии
- Что такое корреляция
- Численное выражение корреляционной зависимости
- Прямая и обратная
- Сильная и слабая
- Корреляционный анализ в психологии
- Коэффициенты Пирсона и Спирмена
- Как рассчитать коэффициент корреляции
- Расчет с помощью электронных таблиц Microsoft Excel
- Расчет с помощью программы STATISTICA
- Использование корреляционного анализа в дипломных работах по психологии (пример)
ПОНЯТИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ
Психолога нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых группах. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или с чем больше связан уровень умственного развития учащихся – с их успеваемостью по математике или литературе и т.п.?
Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г.
Первоначальное значение термина «корреляция» – взаимная связь (Oxford Advanced Learner’s Dictionary of Current English, 1982). Когда говорят о корреляции, используют термины «корреляционная связь» и «корреляционная зависимость».
Корреляционная связь – это согласованные изменения двух признаков или большего количества признаков (множественная корреляционная связь). Корреляционная связь отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого. С другой стороны, корреляционная связь может говорить не о зависимости признаков между собой, а о зависимости этих признаков от другого (других). Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков, нам неизвестно.
Корреляционная зависимость – это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.
Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин.
Говорить в строгом смысле о зависимости мы можем только в тех случаях, когда сами оказываем какое–то контролируемое воздействие на испытуемых или так организуем исследование, что оказывается возможным точно определить интенсивность не зависящих от нас воздействий.
Независимые переменные –воздействия, которые можно качественно определить или даже измерить.
Зависимые переменные –признаки, которые измеряются и могут изменяться под влиянием независимых переменных.
Согласованные изменения независимой и зависимой переменных действительно могут рассматриваться как зависимость.
Корреляционные связи различаются по форме, направлению и степени (силе).
По форме корреляционная связь может быть линейной и криволинейной.
Линейнаясвязь – если с увеличением или уменьшением одной переменной, вторая переменная в среднем либо также растет, либо убывает (рис. 9.1, 9.2). Например, прямолинейной можно назвать связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии.
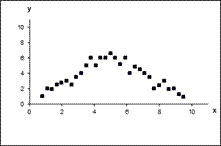
Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи. При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности (рис.9.3).

При положительной (прямой) корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака – низкие значения другого (рис. 9.1).
При отрицательной (обратной) корреляции высокие значения одного признака соответствуют более низким значениям другого (рис. 9.2).
Рис.9.1.Линейная положительная связь Рис.9.2. Линейная отрицательная связь
Рис. 9.3. Криволинейная связь Рис. 9.4. Случайная связь
Степень (сила или теснота) корреляционной связи определяется по величине коэффициента корреляции, обозначающегося часто как r. Величина коэффициента корреляции находится в диапазоне от -1 до +1.
Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.
Используются две системы классификации корреляционных связей по их силе: общая и частная.
Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):
| 1) сильная, или тесная 2) средняя 3) умеренная 4) слабая 5) очень слабая | при r > 0,70; при 0,50 0,70, а не просто корреляция высокого уровня значимости. Переменные могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции. В таблице 9.1 представлены соотношения между шкалами [3].
Все эмпирические меры тесноты связи, кроме коэффициента ранговой корреляции, могут быть заменены методами сопоставления и сравнения. 9.2 КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ rS СПИРМЕНА Источник Обратная корреляция 2021Table of Contents:Что означает «обратная корреляция»Обратная корреляция, также известная как отрицательная корреляция, является противоположной взаимосвязью между двумя переменными, так что они движутся в противоположных направлениях. Например, при переменных A и B при увеличении A B уменьшается и при уменьшении A увеличивается B. В статистической терминологии обратная корреляция обозначается коэффициентом корреляции «r», имеющим значение от -1 до 0, при этом r = -1 указывает на идеальную обратную корреляцию. РАЗРЕШЕНИЕ «Обратная корреляция»Пример расчета обратной корреляцииРасчет корреляции важен, поскольку выгоды от диверсификации портфеля рисков зависят от этой статистики. В приведенном ниже примере показано, как рассчитать статистику. Предположим, что аналитику необходимо вычислить корреляцию для следующих двух наборов данных: X: 55, 37, 100, 40, 23, 66, 88 Y: 91, 60, 70, 83, 75 , 76, 30 В поиске корреляции есть три шага. Сначала добавьте все значения X, чтобы найти SUM (X), соберите все значения Y, чтобы найти SUM (Y), и умножьте каждое значение X на соответствующее значение Y и суммируйте их, чтобы найти SUM (X, Y): SUM (Y ^ 2) = (91 ^ 2) + (60 ^ 2) + (70 ^ 2) + … (30 ^ 2) = 35, 971 Отмечая, что существует семь наблюдений n, может быть использован для нахождения коэффициента корреляции r: r = (nx (SUM (X, Y) — (SUM (X) x (SUM (Y))) / Квадратный корень ((nx SUM (X ^ 2) — SUM (X ) ^ 2) x (nx SUM (Y ^ 2) — SUM (Y) ^ 2)) В этом примере корреляция: r = (7 x 26, 926 — (409 x 485) / Квадратный корень ((7 x 28, 623 — 409 ^ 2) x (7 x 35, 971 — 485 ^ 2)) = 9, 883/23, 414 = -0.42 Два набора данных имеют обратную корреляцию -0. 42. Источник Понятие корреляционной связиТермин «корреляция» (от латинского correlatio – соотношение, взаимосвязь) применяется в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предметов, функций. Широкое распространение в науке термин «корреляция» получил благодаря работам английского ученого-естествоиспытателя Френсиса Гальтона (1822-1911 гг.). В 1888 году Ф. Гальтон сформулировал свои представления о корреляции в работе «Корреляция и ее измерение». Продолжил научную работу в области корреляции британский ученый Карл Пирсон (1857-1936 гг.). Идеи Пирсона о корреляции были опубликованы в серии из 18 книг (между 1893 и 1912 гг.) под заголовком «Математический вклад в теорию эволюции». Также результатом его работы явился широко известный коэффициент корреляции Пирсона. Корреляционная связь — это согласованные изменения двух признаков или большего количества признаков (множественная корреляционная связь). Корреляционная связь отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого. О силе и направленности корреляционной связи мы можем судить по значению коэффициента корреляции. Коэффициент корреляции — статистический показатель степени (силы) и направленности взаимосвязи между двумя переменными. Коэффициент корреляции мы можем определить с помощью корреляционного анализа. Корреляционным анализом называется совокупность методов обнаружения корреляционной связи между случайными величинами или признаками. Корреляционный анализ — это проверка гипотез о связях между переменными. Задача корреляционного анализа сводится к установлению направления (положительного или отрицательного) и формы связи (линейной, криволинейной) между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции. Необходимо отметить, что согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зависимости этих признаков между собой, а о зависимости обоих этих признаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании. Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков, или она оказывается за пределами исследуемой пары признаков — установить этот факт с помощь корреляционного анализа невозможно. Найти причину изменений мы можем с помощью дополнительных исследований и обработки данных, например, с помощью дисперсионного анализа. Корреляционные связи различаются по форме, направлению и степени (силе). По формекорреляционные связи могут быть прямолинейными или криволинейными. В свою очередь прямолинейная корреляционная связь может различаться по направлению и быть прямой (положительной) или отрицательной (обратной) (см. рис. 9.1). Рис. 9.1 Схема прямолинейных корреляционных связей: а) положительная (прямая) корреляционная связь; б) отрицательная (обратная) корреляционная связь В случае прямой или положительной корреляции взаимосвязь характеризуется тем, что высокие значения одной переменной связаны с высокими значения другой, а также низкие значения первой переменной – с низким значениями второй. Графически такая связь представляется прямой линией, отсюда ее более короткое название – линейная связь. В качестве примера можно привести взаимосвязь роста человека и его веса, т.е. чем выше человек тем, как правило, он больше весит, и наоборот чем меньше рост, тем меньше вес. Отрицательная корреляция означает обратную взаимосвязь. Высокие значения одной переменной связаны с низкими значениями другой, и наоборот. Например, у людей с высокой тревожностью, как правило, низкая самооценка. О том, с каким направлением корреляции (положительной или отрицательной) мы имеем дело, можно судить по знаку коэффициента корреляции. При положительной корреляции коэффициент корреляции имеет положительный знак, например r = +0,87, при отрицательной корреляции — отрицательный знак, например r = – 0,87. При криволинейных связях с возрастанием значения одного признака возрастание (или убывание) другого признака происходит неравномерно, или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.). Например, криволинейной может быть связь между уровнем возбуждения и результативностью выполнения задания. Сложные задания выполняются хорошо при среднем уровне возбуждения, но гораздо хуже при очень низком или очень высоком (см. например, Anderson, 1990). При очень низком уровне возбуждения у человека недостаточно сил, чтобы работать над заданием, а очень высокое возбуждение мешает эффективной обработке информации, требующейся для выполнения работы (см. рис. 9.2). Рис. 9.2 Криволинейная корреляционная связь Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции r = +1,00 или r = –1,00; минимальное r = 0. Если коэффициент корреляции по модулю оказывается близким к +1,00 или – 1,00 то это соответствует высокому уровню связи между переменными, а близким к нулю — низкому уровню связи. Величина коэффициента линейной корреляции не может превышать + 1 и быть меньше чем – 1. Эти два числа +1 и – 1 являются границами для коэффициента корреляции. Когда при расчете получается величина большая + 1 или меньшая – 1 то, это свидетельствует о том, что произошла ошибка в вычислениях. Источник Корреляции в дипломных работах по психологииТермин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии. В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии. Что такое корреляцияКорреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере. Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше». Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна). Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие? Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная. В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность. Численное выражение корреляционной зависимостиИтак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение. Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием. Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться. Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
Прямая и обратнаяЗнак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад — выше продажи. Такая корреляция называется прямой, или положительной. Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия. Сильная и слабаяКорреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее. Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше. Максимально возможная сила зависимости – это 1 или -1. Как это понять и представить? Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов. Испытуемый IQ Успеваемость (баллы) Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет. Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1. Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10). Испытуемый IQ Успех в общении с противоположным полом (баллы) Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет. Это пример полной согласованности изменения двух показателей в группе — максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1. А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места. Испытуемый IQ Длина прыжка с места (м) Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0. Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
Если оценить по этой шкале полученную нами выше корреляцию между чтением и благополучием, то окажется, что эта зависимость сильная и отрицательная -0,76. То есть, наблюдается сильная отрицательная связь между начитанностью и благополучием. Что еще раз подтверждает библейскую мудрость о соотношении мудрости и печали. Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях. Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение). Корреляционный анализ в психологииКорреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли? В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения. В психологии иная ситуация. Например, психологи публикуют данные о связи теплых отношений в детстве с родителями и уровня креативности во взрослом возрасте. Означает ли это, что любой из испытуемых с очень теплыми отношениями с родителями в детстве будет иметь очень высокие творческие способности? Ответ однозначный – нет. Здесь нет закона, подобного физическому. Нет механизма влияния детского опыта на креативность взрослых. Это наши фантазии! Есть согласованность данных (отношения – креативность), но за ними нет закона. А есть лишь корреляционная связь. Психологи часто называют выявляемые взаимосвязи психологическими закономерностями, подчеркивая их вероятностный характер — не жесткость. Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места. Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи. Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола. Коэффициенты Пирсона и СпирменаРассмотрим два метода расчета. Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат. В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат. Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных. Как рассчитать коэффициент корреляцииКоэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов. Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ. Расчет с помощью электронных таблиц Microsoft ExcelВернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel. Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические». Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков. Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему. В таблицах Excel реализована формула расчета только коэффициента Пирсона. Расчет с помощью программы STATISTICAЗаносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат. Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны. Использование корреляционного анализа в дипломных работах по психологии (пример)Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах). Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
Таким образом, слова «взаимосвязь», «влияние» и «факторы» — верные признаки того, что методом анализа данных в эмпирическом исследовании должен быть корреляционный анализ. Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков». 1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:
Источник |