Что значит нулевая начальная скорость

Движение тела без начальной скорости

Средняя оценка: 4.4

Всего получено оценок: 105.

Средняя оценка: 4.4

Всего получено оценок: 105.

Во многих случаях тело начинает движение из состояния покоя, то есть, из состояния с нулевой начальной скоростью. Поговорим кратко о движении тела без начальной скорости.

Начальная скорость тела в Системе Отсчета

Описание движения тела начинается с определения Системы Отсчета – то есть с определения тела отсчета, координатных осей и метода измерения времени.

Рис. 1. Система отсчета.

При этом возможны случаи, когда скорость тела в нулевой момент времени равна нулю. То есть, тело в начальный рассматриваемый момент времени не движется относительно тела отсчета (хотя, оно может двигаться в других системах).

Например, пассажир движущегося поезда некоторое время сидит на своем месте, а потом переходит на другое место. В Системе Отсчета, связанной с рельсами, он постоянно движется. Однако, в Системе Отсчета, связанной с вагоном, он в нулевой момент времени покоится, и лишь спустя некоторое время начинает движение.

Рис. 2. Поезд, пассажир, относительность движения.

Таким образом, начальная скорость тела зависит от выбранной Системы Отсчета.

Формулы кинематики для случая нулевой начальной скорости

Если начальная скорость тела равна нулю, а тело через некоторое время переместилось, значит, на тело действовала некоторая сила, которая привела к появлению ускорения, в результате которого и произошло перемещение тела. Иначе говоря, тело двигалось с ускорением. То есть, можно использовать общие формулы кинематики для равноускоренного движения:

$$\overrightarrow x=\overrightarrow x_0+\overrightarrow v_0t+<\overrightarrow at^2\over 2>$$

$$\overrightarrow v=\overrightarrow v_0+\overrightarrow at$$

Подставив в эти формулы $\overrightarrow v_0 = 0$, получим:

$$\overrightarrow v=\overrightarrow at$$

Если построить графики этих формул и сравнить их с общими графиками, то можно отметить следующие особенности.

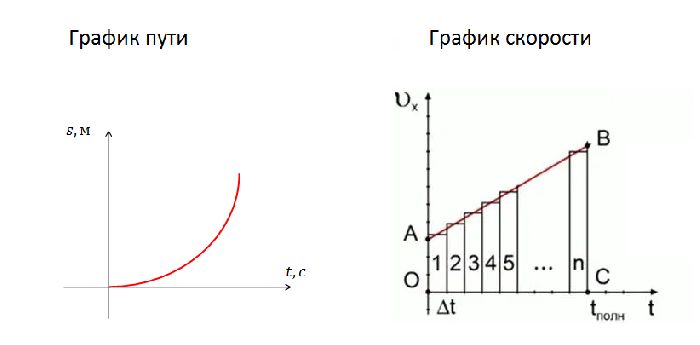
График пути представляет собой параболу, такую же, как при движении с начальной скоростью. Однако, эта парабола симметрична относительно оси ординат, и ее вершина пересекает эту ось. Следовательно, если тело двигалось с тем же ускорением до принятого в Системе Отсчета начального момента, то в этот момент перемещение тела имеет экстремальное (наибольшее или наименьшее) значение. Например, если рассматривается свободное падение тела, то нулевой момент будет соответствовать высшей точке траектории.

График скорости представляет собой прямую, имеющую тот же наклон, как и при движении с начальной скоростью, но, пересекающую начало координат.

Рис. 3. Графики пути и скорости для равноускоренного движения.

Выбор Системы Отсчета

Формулы, описывающие движение тела без начальной скорости, проще. Поэтому при решении задач следует, по возможности, выбирать Систему Отсчета так, чтобы у рассматриваемого тела начальная скорость была равна нулю.

Особенно простая форма получается, если и начальное перемещение тела также будет нулевым. Например, для описанного выше примера перехода пассажира с одного места на другое – Систему Отсчета разумно связать с креслом пассажира.

Что мы узнали?

Формулы кинематики для движения без начальной скорости проще. Поэтому следует по возможности выбирать Систему Отсчета так, чтобы рассматриваемые тела в этой системе не имели начальной скорости.

Источник

Как найти нулевую скорость

В курсе физики помимо обычной скорости, знакомой всем из алгебры, существует понятие «нулевая скорость». Нулевая скорость или, как ее еще называют, – начальная находится другим способом, отличным от формулы нахождения обычной скорости.

Нулевую скорость можно найти несколькими способами, каждый из которых применим к задачам, содержащим те или иные известные компоненты.

Если в условии задачи даны расстояние, которое прошло тело (S), время, которое потребовалось телу для преодоления расстояния (t), ускорение, с которым двигалось тело (a), то найти нулевую скорость можно с помощью формулы: S=V0t+at^2/2, где V0 – нулевая скорость, t^2 – t в квадрате. Пусть S=100 м, t=5 c, a=2 м/c в квадрате.

Чтобы найти нулевую скорость (V0) с помощью формулы, указанной выше, воспользуйтесь правилом нахождения неизвестного слагаемого: «Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое». Получится: V0t= S- at^2/2.

Затем примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Получится: V0= (S- at^2/2)/t.

В полученную формулу подставьте значения известных величин. Получится: V0=(100-2х5^2/2)/5, V0=(100-25)/5, V0=15 м/с.

Когда в условии задачи вместо расстояния (S) дана конечная скорость (V), к которой тело пришло от нулевой скорости (V0), то для нахождения V0 используйте формулу: V=V0+at, где V – конечная скорость тела, а – ускорение, с которым двигалось тело, t – время, на протяжении которого двигалось тело. Пусть V=25 м/c, t=5 c, a=2 м/c в квадрате.

Теперь для нахождения нулевой скорости воспользуйтесь правилом неизвестного слагаемого. Получится: V0= V- at. В полученную формулу подставьте известные значения. Таким образом: V0=25-2х5, V0=25-10, V0=15 м/с.

Источник

Формула нахождения нулевой скорости

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение – частный случай равноускоренного движения с ускорением, равным нулю.

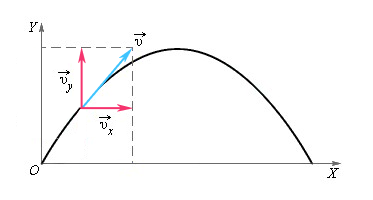
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 – начальная скорость тела, a = c o n s t – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

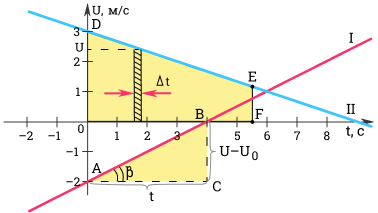
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v – v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = – 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = – 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v – v 0 ) 2 t .

Мы знаем, что v – v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 – v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.

Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.

Скорость является функцией времени и определяется как абсолютной величиной, так и направлением. [1] Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.

Сегодня изучали тему «Равноускоренное прямолинейное движение»
Нам сказали 3 формулы по теме:
Ускорение: A
Скорость: V
Расстояние: S
Время: t
А в задаче дано S и V, надо найти V нулевое (нач. скорость) и a (ускорение)
Как найти «a» формула есть, но нужно сначала найти V нулевое, а этой формулы нам не дали 🙁
Кто знает напишите.. .

То есть нужна формула V нулевого По теме )

P.S. Кому не лень, напишите решение задачи:
«Поезд, двигаясь под уклон, прошёл за 20с путь 340м и развил скорость 19 м/с. С каким ускорением двигался поезд и какой была скорость в начале уклона? «(10 класс)

v=v0+at – это понятно, ня?
s=v0*t+at^2/2

имеем ДВА уравнения с двумя переменными
Решаем
vt=V0*t+at^2
s=v0*t+at^2/2

a=2*(380-340)/20^2=80/400=0.2 м/с^2
v0=v-at=19-0.2*20=15

Источник

Как найти нулевую скорость

В курсе физики помимо обычной скорости, знакомой всем из алгебры, существует понятие «нулевая скорость». Нулевая скорость или, как ее еще называют, – начальная находится другим способом, отличным от формулы нахождения обычной скорости.

Нулевую скорость можно найти несколькими способами, каждый из которых применим к задачам, содержащим те или иные известные компоненты.

Если в условии задачи даны расстояние, которое прошло тело (S), время, которое потребовалось телу для преодоления расстояния (t), ускорение, с которым двигалось тело (a), то найти нулевую скорость можно с помощью формулы: S=V0t+at^2/2, где V0 – нулевая скорость, t^2 – t в квадрате. Пусть S=100 м, t=5 c, a=2 м/c в квадрате.

Чтобы найти нулевую скорость (V0) с помощью формулы, указанной выше, воспользуйтесь правилом нахождения неизвестного слагаемого: «Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое». Получится: V0t= S- at^2/2.

Затем примените правило нахождения неизвестного множителя: «Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель». Получится: V0= (S- at^2/2)/t.

В полученную формулу подставьте значения известных величин. Получится: V0=(100-2х5^2/2)/5, V0=(100-25)/5, V0=15 м/с.

Когда в условии задачи вместо расстояния (S) дана конечная скорость (V), к которой тело пришло от нулевой скорости (V0), то для нахождения V0 используйте формулу: V=V0+at, где V – конечная скорость тела, а – ускорение, с которым двигалось тело, t – время, на протяжении которого двигалось тело. Пусть V=25 м/c, t=5 c, a=2 м/c в квадрате.

Теперь для нахождения нулевой скорости воспользуйтесь правилом неизвестного слагаемого. Получится: V0= V- at. В полученную формулу подставьте известные значения. Таким образом: V0=25-2х5, V0=25-10, V0=15 м/с.

Источник

Большая Энциклопедия Нефти и Газа

Линия — нулевая скорость

Линия нулевых скоростей показана на рис. 21.11. Между вальцом и транзитной частью потока происходит постоянный обмен частицами, которые из вальца попадают в транзитную часть и уносятся вниз по течению. Но и частицы из транзитной части поступают в валец и могут находиться там в движении, пока не будут унесены транзитной частью потока. [1]

Оно будет расти ( линия Up) до тех пор, пока точка состояния не пересечет линию GH нулевой скорости ползучести , а затем начнет падать ( асимптотически) до нуля, как при обычной релаксации. [2]

Линия, начинающаяся в точке отрыва и соединяющая точки с нулевой скоростью внутри вязкого слоя, отошедшего от стенки, может быть определена как линия нулевой скорости ( фиг. [3]

В отношении параметра относительного стеснения траншеи и его учета в практических расчетах необходимо отметить следующее: при расположении трубопровода вне циркуляционной зоны отношение D / hT не влияет на Сжт и С т ( условие обтекания приближается к случаю обтекания трубопровода, расположенного на дне транзитного потока); при расположении трубопровода в циркуляционной зоне стеснение траншеи трубопроводом, как показали опыты, несущественно влияет на Сжт и Сут, если верхняя образующая трубопровода расположена ниже линии нулевых скоростей циркуляционной зоны . При расположении цилиндра в пределах циркуляционной области значение СХт отрицательно; положительные значения Сжт были получены, когда цилиндр находился вне циркуляционной области. [4]

В теории Чепмена предполагается, что воздух из области возвратного течения с малой скоростью попадает в отделившийся пограничный слой при температуре, равной температуре стенки. Бели бы это предположение было правильным, то насадок должен был бы измерить на линии нулевой скорости температуру, равную температуре стенки, однако, согласно измерениям насадком у стенки, разность температур на порядок величины меньше принятой в теории. По результатам измерений насадками толщина свободного слоя больше половины глубины области отрыва, что также может быть причиной расхождений, поскольку в теории Чепмена предполагается, что толщина относительно мала. Таким образом, теория должна быть модифицирована с учетом возвратного течения. [5]

Существуют три серии таких кривых для различных значений с, обратная величина которых приблизительно пропорциональна толщине охлажденного слоя, окружающего пузырь. Для каждого значения с имеются три кри вые радиус — время для различных значений температуры в объеме жидкости, и, наконец, все эти кривые соединялись линиями нулевой скорости . [6]

При исследовании принято наиболее неблагоприятное с точки зрения образования зон аэродинамической тени расположение моделей главного корпуса: продольные оси моделей зданий ориентированы нормально к набегающему потоку. Перед зданием поток тормозится. Над зданием и за ним в зоне выше линии нулевых скоростей наблюдается увеличение скорости. [8]

Верхняя зона — поверхностная, которую называют водоворотной областью, или вальцом. Частицы жидкости в вальце находятся в сложном движении, которое происходит под действием поступательно движущейся части потока и силы тяжести. На некотором заглублении от поверхности осредненные скорости равны нулю. Линия нулевых скоростей показана на рис. 21.11. Между вальцом и транзитной частью потока происходит постоянный обмен частицами, которые из вальца попадают в транзитную часть и уносятся вниз по течению. Но и частицы из транзитной части поступают в валец и могут находиться там в движении, пока не будут унесены транзитной частью потока. На замену им поступят другие частицы. [9]

Горячий внешний след за тупым телом образован сжатым и разогретым в ударном слое газом, прошедшим через почти нор-мальный к потоку участок головного скачка уплотнения. Внутренний след образован турбулентным течением, возникающим в области с наибольшим градиентом скорости, и смыкающимся с ним свободным вязким слоем, сходящим с поверхности тела. Линия нулевого значения скорости, на которой касательная составляющая скорости равна нулю, начинается в точке отрыва на теле и поворачивает обратно в горловине следа, поскольку при выравнивании потока давление возрастает. Газ над линией нулевой скорости в дальнейшем образует внутренний след. [10]

По вертикали увеличение интенсивности турбулентности по отношению к начальному значению простирается примерно на ( 2 — 2 2) Язд практически независимо от начальной турбулентности набегающего потока. Характеризуя в целом полученные результаты, необходимо отметить, что главный корпус АЭС существенно изменяет параметры набегающего потока, сильно турбулизнруя его. Как показали проведенные исследования, картина обтекания главных корпусов получается весьма сложной: На рис. 13.12 представлены профили скорости ветра в плоскости по оси вентиляционных труб реакторного зала и по оси машинного зала. В плоскости по оси машинного зала линия смены знака скорости ( линия нулевых скоростей ) находится выше отметки крыши машинного зала, что свидетельствует о существовании в пространстве между корпусами вихревых циркуляционных зон. В нижней части этих зон под линией нулевых скоростей поток движется в сторону, противоположную направлению движения основного набегающего потока. [11]

По вертикали увеличение интенсивности турбулентности по отношению к начальному значению простирается примерно на ( 2 — 2 2) Язд практически независимо от начальной турбулентности набегающего потока. Характеризуя в целом полученные результаты, необходимо отметить, что главный корпус АЭС существенно изменяет параметры набегающего потока, сильно турбулизнруя его. Как показали проведенные исследования, картина обтекания главных корпусов получается весьма сложной: На рис. 13.12 представлены профили скорости ветра в плоскости по оси вентиляционных труб реакторного зала и по оси машинного зала. В плоскости по оси машинного зала линия смены знака скорости ( линия нулевых скоростей) находится выше отметки крыши машинного зала, что свидетельствует о существовании в пространстве между корпусами вихревых циркуляционных зон. В нижней части этих зон под линией нулевых скоростей поток движется в сторону, противоположную направлению движения основного набегающего потока. [12]

Источник