Что значит нормализация числа

Нормализованная запись числа

Нормализованная запись отличного от нуля действительного числа – это запись вида Где q – целое число (положительное, отрицательное или ноль) m – правильная Р-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть: Примеры записи десятичных чисел: Примеры записи двоичных чисел: Умножением двоичных чисел мы пока не занимались, поэтому вам может быть не понятно, почему 1 = 0,1 * 2 1 . Объяснять подробности здесь не будем, просто имейте ввиду, что в двоичной системе умножение на два в какой-либо степени – это сдвиг разрядов. Если число умножается на 2 в какой-то степени, и если эта степень – целое положительное число, то это будет сдвиг влево на количество разрядов, которое соответствует степени числа два. То есть Как нетрудно догадаться, деление – это сдвиг вправо. Например,

Число НОЛЬ не может быть записано в нормализованной форме в том виде, в котором мы её определили. Поэтому считаем, что нормализованная запись нуля в десятичной системе будет такой:

Нормализованная экспоненциальная запись числа – это запись вида Где q – целое число (положительное, отрицательное или ноль) m – правильная Р-ичная дробь, у которой целая часть состоит из одной цифры, при этом m – это мантисса числа, а q – порядок (или экспонента) числа.

Описанные выше примеры в нормализованной экспоненциальной записи будут выглядеть так, как показано ниже.

Примеры записи десятичных чисел: Примеры записи двоичных чисел: Обратите внимание, что в нормализованной форме первая цифра после запятой НЕ может быть нулём, а в нормализованной экспоненциальной форме это допускается.

Источник

Нормализация данных с помощью простых чисел

В данной публикации рассмотрен простой и эффективный алгоритм нормализации данных с помощью простых чисел. Нормализация данных широко используется при шифровании, архивировании данных, а также может иметь некоторые другие практические применения, поэтому я надеюсь, что изложенный в статье материал будет полезен читателям. Также, в качестве примера, приведён пример кода на языке С++ реализующий описанный в статье метод нормализации данных.

Краткое описание алгоритма нормализации данных

Ряд натуральных чисел N = <1, 2, 3, :. n>, n = 1, µ можно разложить в виде суммы произвольного количества рядов, следующего вида:

Очевидно, что часть рядов составляющих сумму натурального ряда, будут содержать не более одного простого числа, которое является первым элементом последовательности и их можно исключить из рассмотрения при поиске простых чисел. Так каждая из следующих шести последовательностей будет содержать столько же простых чисел, сколько и натуральный ряд.

Пусть P = <1,2,3,5,7,11,13,17,19,23,29, : P n >, n = 1, µ ряд простых чисел. Рассмотрим представление натурального ряда в виде суммы следующего количества рядов P 2 * P 3 * :. * Pn , n = 2, ? за исключением рядов, содержащих не более одного простого числа.

Для примера на рисунке ниже наглядно показано разложение натурального ряда в виде 30-ти рядов (P 2 * P 3* P 4 = 2*3*5 = 30), только 8-мь из которых содержат простые числа. Исключаемые из рассмотрения последовательности выделены цветом.

Как видно из рисунка, после разложения натурального ряда мы получили некоторую последовательность, состоящую из 8-ми рядов и содержащую в себе все простые числа, за исключением 2, 3 и 5.

Также отметим, что в полученной нами последовательности нет ни одного элемента кратного 2, 3 или 5. Очевидно, что данную последовательность можно также получить, проверяя каждое из натуральных чисел на кратность 2, 3 или 5.

Далее рассмотрим вопрос о соотношении чисел в данной последовательности к общему числу натуральных чисел. Нетрудно посчитать, что в данном случае оно равно отношению выбранного и общего количества рядов при разложении натурального ряда N, что составляет 8/30 или 26,67% от общего количества натуральных чисел.

В общем случае, данное отношение можно вычислить по следующей формуле:

В таблице ниже приведены расчеты % для различных последовательностей.

Из таблицы видно, что последовательность, не содержащая чисел кратных 2,3,5,7,11 , составляет 20,78 % натуральных чисел, а последовательность не содержащая чисел кратных 2,3,5,7,11, :, 197, 199 только 10,39 % натуральных чисел. Если числа принадлежащие только первой последовательности обозначить 0, а числа, принадлежащие и первой и второй последовательности, 1 то мы получим бесконечную периодическую последовательность из 0 и 1, элементы которой будут повторяться через 8.8E+81 . Следует отметить, что соотношение 0 и 1 в полученной последовательности будет примерно равным.

Далее приведен пример кода на С++, использующий данную последовательность из 0 и 1, для нормализации данных:

Откомпилируйте приведённый выше код любым компилятором языка C/C++ (рекомендуется использовать MS Visual C++ ) или загрузите скомпилированную версию отсюда .

Выполните команду s2310.exe 23365444532 ваш_файл нормализованный_файл для нормализации файла. В результате получится некоторый нормализованный (зашифрованый) файл, соотношениие 0 и 1 в котором будет почти одинаковое. Число 23365444532 выбрано случайным образом, это 64-bit беззнаковое целое является ключом для востановления исходного файла. Не зная данного числа, востановить исходный файл невозможно.

Чтобы востановить исходный файл выполните команду

В качестве ключа для нормализации/востановления данных Вы можете использовать произвольное 64-bit беззнаковое целое число. На тестах данный метод нормализации данных показал хорошие результаты, т.е. в получаемом файле соотношение 0 и 1 всегда почти точно 50% на 50%, в не зависимости от соотношение 0 и 1 в исходном файле.

Источник

Что значит нормализация числа

Нормализованная запись отличного от нуля действительного числа — это запись вида a= m*P q , где q — целое число (положительное, отрицательное или ноль), а m — правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть . При этом m называется мантиссой числа, q — порядком числа.

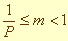
Примеры:

1. 3,1415926 = 0, 31415926 * 10 1 ;
2. 1000=0,1 * 10 4 ;
3. 0,123456789 = 0,123456789 * 10 0 ;
4. 0,0000107₈ = 0,1078 * 8 -4 ; (порядок записан в 10-й системе)
5. 1000,0001₂ = 0, 100000012 * 2 4 .

Так как число ноль не может быть записано в нормализованной форме в том виде, в каком она была определена, то считаем, что нормализованная запись нуля в 10-й системе будет такой:
0 = 0,0 * 10 0 .

Нормализованная экспоненциальная запись числа — это запись вида a= m*P q , где q — целое число (положительное, отрицательное или ноль), а m — P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q — порядком числа.

Представление чисел с плавающей запятой.

При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды — для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, был придуман так называемый смещённый порядок, который рассчитывается по формуле 2 a-1 +ИП, где a — количество разрядов, отводимых под порядок.

Пример:
Если истинный порядок равен -5, тогда смещённый порядок для 4-байтового числа будет равен 127-5=122.

Источник

Кодирование вещественных чисел. Нормализованное представление числа

В компьютерной технике вещественными называются числа, имеющие дробную часть.

Дробные числа могут содержать большой набор цифр. Например: 0.0000345 или 10900000 (т.е очень большие или очень маленькие числа). Для удобства вещественные числа приводят к виду так называемого нормализованного представления числа. Заключается такое представление в том, что число записывается в виде произведения на основание системы счисления, возведенное в ту или иную степень. Например, предыдущие два числа в нормализованном виде будут выглядеть так: 0.345 * 10 -4 и 0.109 * 10 8 . Здесь числа 0.345 и 0.109 – мантиссы вещественных чисел, 10 – основание системы счисления, а -4 и 8 – порядки. При этом запятая (точка), разделяющая дробную и целую части ставится перед первой значащей цифрой (отличной от 0).

Нормализованная форма числа является наиболее удобной для представления дробных чисел в компьютере.

Понятно, что нормализированное представление используется не только для десятичной системы счисления. Вот примеры нормализованных записей дробных чисел в двоичной системе счисления:

101.11 = 0.10111 * 2 11
0.001 = 0.1 * 2 -10

Здесь степени 11 и 10 – это двоичная форма десятичных чисел 3 и 2.

Нормализованная форма представления числа – это одна из форм множества вариантов экспоненциальной формы записи числа.

Пусть слово состоит из 2 байт, два слова – это 4 байта или 32 бита.

Нормализированное число одинарной точности, представленное в формате с плавающей точкой, записывается в память следующим образом: знак числа – в бите 15 первого слова (0 – для положительных и 1 – для отрицательных чисел); порядок размещается в битах 7-14 первого слова, а мантисса занимает остальные 23 бита в двух словах (с 0 по 6 бит первого слова и все биты второго слова). Нормализированное число двойной точности записывается в четыре слова памяти и отличается от представления чисел с одинарной точностью только тем, что продолжение мантиссы размещается в следующих за первым словом трех последовательных словах памяти, а всего под мантиссу в этом случае отводится 55 бит.

Порядок числа, представленного в формате с плавающей точкой, изменяется в диапазоне от -128 до +127 и запоминается увеличенным на 128. Такой способ представления порядка называется смещенным.

Следует иметь в виду, что, хотя для мантиссы отведено 23 разряда для чисел одинарной точности и 55 разрядов – для чисел двойной точности, в операциях участвует 24 и 56 разрядов соответственно, т.к. старший разряд мантиссы нормализированного числа не хранится, т.е. имеет место так называемый скрытый разряд. Однако при аппаратном выполнении операций этот разряд автоматически восстанавливается и учитывается. Порядок числа также учитывает скрытый старший разряд мантиссы.

Нормализованная мантисса в двоичной системе счисления всегда представляется десятичным числом m , лежащим в диапазоне 0,5 .

Пример представления числа в формате с плавающей точкой:

Если мантисса представлена бесконечной периодической дробью, то последний учитываемый разряд мантиссы округляется.

При выполнении арифметических операций над числами, представленными в формате с плавающей точкой, надо отдельно выполнять их для порядков и мантисс. При алгебраическом сложении чисел надо сначала уравнять порядки слагаемых. При умножении порядки надо складывать, а мантиссы — перемножать. При делении из порядка делимого вычитают порядок делителя, а над мантиссами совершают обычную операцию деления. После выполнения операций, если это необходимо, проводят нормализацию результата, что влечет изменение порядков, т.к. каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо увеличению на единицу. Введение термина «плавающая точка» как раз и объясняется тем, что двоичный порядок, определяющий фактическое положение точки в изображении числа, корректируется после выполнения каждой арифметической операции, т.е. точка в изображении числа «плавает» (изменяется ее положение) по мере изменения данной величины. А в изображении чисел, представленных в формате с фиксированной точкой, она жестко зафиксирована в определенном месте.

Арифметические операции с числами, представленными в формате с плавающей точкой, намного сложнее таких же операций для чисел, представленных в формате с фиксированной точкой. Но зато плавающая точка позволяет производить операции масштабирования автоматически в самой машине и избавляет от накопления абсолютной погрешности при вычислениях (хотя не избавляет от накопления относительной погрешности).

Источник

Математические основы информатики

Представление вещественных чисел

Вещественные числа в компьютере хранятся в формате с плавающей запятой, который опирается на нормализованную форму записи чисел.

Нормализованная запись числа

Если при представлении целых чисел в компьютере ограничением может служить лишь величина записываемого числа, то при записи вещественного числа речь в первую очередь идет о точности его представления, т. е. о количестве значащих цифр, которые удается сохранить в ограниченном числе разрядов.

Пример 6. Допустим, мы имеем калькулятор, в котором на экране дисплея для вывода чисел есть только 10 знакомест (включая знак числа и запятую между целой и дробной частями десятичного числа). Если нам необходимо работать с числами

-6392000000; -639,2; -0,0000006392,

то на дисплее нашего калькулятора отобразить удастся лишь второе из них (первое число занимает 11 знакомест, второе — 6 знакомест, третье — 13 знакомест).

Эта задача может быть решена» если числа представить несколько иначе. Забегая вперед, скажем, что для примера 6 искомый способ записи чисел в калькуляторе таков :

-6.392Е+9 -6.392Е+02 -6.392Е — 07,

где знак «Е» читается как «умножить на десять в степени». Такая запись отражает экспоненциальную форму записи чисел.

Определение 3. Любое число а в экспоненциальной форме представляется в виде , где Р — основание системы счисления, т называется мантиссой числа, q — порядком числа.

Пример 7. Длину отрезка, равного 47,8 см, в экспоненциальной форме записи можно представить так:

1) 478 х 10 -1 см = 478 мм;

2) 4,78 х 10 1 см = 4,78 дм;

3) 47,8 х 10 0 см = 47,8 см;

4) 0,478 х 10 2 см = 0,478 м.

Из этого примера видно, что длину одного и того же отрезка можно записать с использованием различных экспоненциальных форм. Эта неоднозначность записи может приводить в определенных случаях к неудобству. Из курса алгебры известно, что если Р фиксировано и 1/Р ≤ m

Определение 4. Нормализованная запись отличного от нуля вещественного числа — это запись вида , где q — целое число (положительное, отрицательное, или ноль), a m — правильная Р-ичная дробь, у которой первая цифра после запятой не равна нулю, т. е. 1/Р ≤ m .

Заметим, что число ноль не может быть записано в нормализованной форме так, как она была определена. Поэтому относительно нормализованной записи нуля приходится прибегать к особым соглашениям. Условимся, что запись нуля является нормализованной, если и мантисса, и порядок равны нулю.

В нормализованной форме все числа записываются одинаково в том смысле, что запятая у них ставится в одном и том же месте — перед первой (самой левой) значащей цифрой мантиссы. Заметим, что в двоичной системе счисления первая цифра мантиссы нормализованного числа всегда равна 1 (за исключением числа ноль). Величина же числа (т. е. ее порядок) указывается отдельно, с помощью соответствующей степени основания системы счисления, в которой это число было записано изначально. Количество цифр в мантиссе может оказаться меньше, чем число значащих цифр в исходном числе. Часто в нормализованной записи мантисса Р-ичного числа записывается в Р-ичной системе счисления, а порядок и само число Р — в десятичной.

Пример 8. Приведем примеры нормализации чисел:

1) 0 = 0,0 х 10 0 (возможная нормализация нуля);

2) 3,1415926 = 0,31415926 х 10 1 (количество значащих цифр не изменилось);

3) 1000 = 0,1 х 10 4 (количество значащих цифр уменьшилось с четырех до одной);

4) 0,123456789 = 0,123456789 х 10 0 (запятую передвигать не нужно);

5) 0,0000107₈ = 0,107₈ х 8 -4 (количество значащих цифр уменьшилось с семи до трех);

6) 1000,0001₂ = 0,10000001₂ х 2 4 (количество значащих цифр уменьшить невозможно);

7) AB,CDEF₁₆ = 0,ABCDEF₁₆ x 16 2 (количество значащих цифр уменьшить невозможно).

При записи нормализованного числа в компьютере или калькуляторе для записи мантиссы и порядка отводится заранее фиксированное количество разрядов.

! В компьютерном представлении вещественных чисел максимально допустимое количество цифр в мантиссе определяет точность, с которой может быть представлено число.

Поясним это на примере школьного калькулятора, который производит вычисления в десятичной системе счисления. Пусть это будет калькулятор с десятью знакоместами на дисплее, мантисса в нем имеет четыре цифры, порядок — две. В отличие от стандартной нормализации, у калькуляторов первая значащая цифра, с которой и начинается мантисса, изображается перед точкой. Порядок при этом соответственно уменьшается на единицу. Такая форма записи нормализованных чисел позволяет экономить одно знакоместо, так как вместо нуля в целой части мы помещаем значащую цифру.

1) Число 248,53786 в калькуляторе превращается в +2.485Е+02. Переводя последнее число в привычное представление с фиксированной запятой, получим +248,5.

2) Число -2485378600,0 в калькуляторе превращается в -2.485Е+09. Переводя последнее число в привычное представление с фиксированной запятой, получим -2485000000.

3) Число 0,00024853786 в калькуляторе имеет вид +2.485Е-04, т. е. равно числу 0,0002485.

Следовательно, всякое десятичное число, состоящее не более чем из четырех значащих цифр в нормализованном виде, можно представить в таком калькуляторе точно, а остальные числа — лишь приближенно.

В первом пункте примера 9 погрешность калькуляторного представления исходного числа составила 248,53786 — 248,5 = 0,03786. Во втором пункте погрешность равна 2485378600 — 2485000000 = 378600, а в третьем — 0,00024853786 — 0,0002485 = 0,00000003786. Если бы мантисса калькулятора имела больше цифр, погрешность была бы меньше.

Определение 5. Модуль разности между значением числа х и неким его представлением х* (компьютерным, калькуляторным) называется абсолютной погрешностью представления х.

Несмотря на то, что в абсолютном исчислении погрешность может быть значительно больше 1, относительно величины самого числа ее порядок остается неизменным. Относительная погрешность представления чисел в примере 9 равна:

Определение 6. Относительной погрешностью представления х называют величину

Вопрос. Как вы думаете, что нам дает знание величин абсолютной и относительной погрешности при решении реальных задач на компьютере?

Ответ. Абсолютная погрешность говорит о том, на сколько полученный результат (например, результат представления числа в компьютере) отличается от истинного результата (в нашем примере — от самого числа).

При решении реальных задач знание этой величины позволяет оценивать, насколько достоверный результат был получен. Если его точность нас не удовлетворяет, то следует выбрать другой (более точный) способ представления чисел.

Относительная же погрешность показывает, сколько верных старших значащих цифр содержит результат. В примере 9 относительная погрешность представления разных по величине чисел равна 0,00015233. Такая относительная погрешность означает, что мы имеем три безусловно верные значащие цифры результата. Значение относительной погрешности непосредственно связано с количеством разрядов, отводимых для представления мантиссы нормализованного числа.

На практике обычно известна относительная погрешность представления чисел, так как разрядность мантиссы фиксирована. Следовательно, можно предположить, сколько верных цифр содержит результат. Если из каких-то априорных соображений известно значение вычисляемой величины, то можно оценить абсолютную погрешность результата.

В компьютерной записи вещественных чисел с плавающей запятой количество цифр, отводимых под запись порядка, определяет, насколько большие и насколько маленькие положительные числа могут быть представлены.

Покажем это опять на примере школьного калькулятора. В формате нашего калькулятора порядок имеет две цифры, и наибольшее число, которое может быть в нем представлено, — это +9.999Е+99. Если бы нам пришлось записать это число в формате с фиксированной запятой, оно имело бы ровно 100 цифр до запятой (четыре девятки и 96 нулей), т. е. это и в самом деле очень большое число.

А самое маленькое положительное число, которое можно ввести в нашем калькуляторе, — это +1.000Е-99. В формате с фиксированной запятой оно имеет 99 десятичных знаков после запятой, а именно 98 нулей и единицу. Это очень маленькое число. Таким образом, выражая порядок лишь двумя десятичными цифрами, можно записывать числа из очень широкого диапазона.

Широкий диапазон представления чисел с плавающей запятой необходим при решении научных и инженерных задач. Такое представление чисел не только позволяет сохранять в разрядной сетке большое количество значащих цифр и тем самым повышать точность вычислений, но также упрощает действия над порядками и мантиссами.

Представление вещественных чисел в формате с плавающей запятой

Как и для целых чисел, при представлении вещественных чисел в компьютере используется чаще всего двоичная система счисления, следовательно, предварительно десятичное число должно быть переведено в двоичную систему, а уж затем представлено в нормализованной форме с Р — 2.

При представлении нормализованных чисел часть разрядов ячейки отводится для записи порядка числа, остальные разряды — для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. О таком представлении говорят, что число записано в формате с плавающей запятой.

Например, можно представить себе такое распределение разрядов ячейки памяти:

Первые два разряда служат для представления знаков порядка (s_q) и мантиссы (s_m) соответственно. Следующие к разрядов используются для представления абсолютной величины порядка числа (q), остальные n разрядов — для представления абсолютной величины мантиссы. В каждом разряде ячейки может храниться одно из двух значений: 0 или 1.

Тогда изображенному на схеме состоянию ячейки соответствует число

При такой системе записи наибольшее по абсолютной величине число, которое может быть представлено в ма шине, равно * (1 — 2 -n ), а наименьшее по абсолютной величине число, отличное от нуля, равно

Вещественных чисел, точно представимых в компьютере, конечное число. Остальные числа либо приближаются представимыми, либо оказываются непредставимыми. Последнее относится к слишком большим и к слишком маленьким вещественным числам.

Выполнение арифметических операций над вещественными числами

Использование в компьютере представления чисел в формате с плавающей запятой усложняет выполнение арифметических операций. При сложении и вычитании чисел сначала производится подготовительная операция, называемая выравниванием порядков. Она состоит в том, что мантисса числа с меньшим порядком сдвигается в своей ячейке вправо на количество разрядов, равное разности порядков данных чисел. После этой операции одноименные разряды мантисс оказываются расположенными в одноименных разрядах обеих ячеек, и теперь уже сложение или вычитание мантисс выполняется достаточно просто, так же как над числами с фиксированной запятой.

Пусть — два нормализованных двоичных числа, и . Результатом их сложения или вычитания будет являться следующее выражение:

После операций над порядками и мантиссами мы получаем порядок и мантиссу результата, но последняя, вообще говоря, может не удовлетворять ограничениям, накладываемым на мантиссы нормализованных чисел. Так как от результата арифметических операций в компьютере требуется, чтобы он также был нормализованным числом, необходимо дополнительное преобразование результата — нормализация. В зависимости от величины получившейся мантиссы результата, она сдвигается вправо или влево так, чтобы ее первая значащая цифра попала в первый разряд после запятой. Одновременно порядок результата увеличивается или уменьшается на число, равное величине сдвига.

Заметим, что над мантиссами в арифметическом устройстве могут выполняться все четыре арифметических действия, а также операции сдвига, тогда как над порядками производятся только действия сложения и вычитания. Отрицательные порядки можно записывать в дополнительном коде для того, чтобы операцию вычитания свести к операции сложения.

В ряде случаев, даже если некоторые два числа были представлены в формате с плавающей запятой абсолютно точно, результат выполнения над ними арифметических операций часто может содержать погрешность, а иногда может быть заведомо неверным.

Поясним более подробно особенности выполнения арифметических операций над вещественными числами на примерах. При этом будем считать, что в записи вещественного числа с плавающей запятой один разряд отводится под десятичный порядок и пять разрядов — под десятичную мантиссу.

Пример 10. Предположим, что требуется сложить следующие числа: 0,23619 х 10 2 и 0,71824 х 10 -1 . Так как порядки у чисел различны, то перед сложением производится выравнивание порядков. Число с меньшим порядком преобразуется в число с порядком, равным порядку другого слагаемого (меньший порядок «приводится» к большему). В данном случае второе слагаемое будет преобразовано к виду 0,00071824 х 10 2 , после чего выполняется сложение.

Результат получили с большим числом разрядов, чем вмещает ячейка, поэтому он округляется и записывает ся в памяти в виде 0,23691 х 10 2 .

Пример 11. Выполним сложение двух вещественных чисел:

0,23619 х 10 8 и 0,91824 х 10 8 . Так как порядки у этих чисел одинаковы, то производить операцию выравнивания порядков не требуется. Операция сложения сводится к сложению мантисс.

Результат — ненормализованное число 1,15443 х 10 8 . Требуется выполнить нормализацию путем сдвига мантиссы вправо на один разряд, а затем округление результата, так как в мантиссе будет уже шесть цифр, а в ячейке памяти под мантиссу отведено их только пять. Ответ: 0,11544 х 10 9 .

Пример 12. Выполним сложение двух вещественных чисел, одно из которых достаточно большое по сравнению со вторым: 0,23619 х 10 3 и 0,91824 х 10 -3 . Так как порядки у этих чисел различны, то требуется произвести предварительную операцию их выравнивания. После выполнения выравнивания порядков складываться будут следующие числа:

После сложения в мантиссе оказалось более пяти значащих цифр и при записи в ячейку памяти произойдет округление результата до 0,23619 х 10 3 . Получившееся число равно первому слагаемому, т. е. при выравнивании порядков все значащие цифры мантиссы второго слагаемого потеряны. Таким образом, мы получили результат, невозможный с точки зрения обычной математики: а + b = а при b > 0. Но в компьютерной арифметике с ограниченным числом разрядов такой результат возможен, и об этом необходимо помнить при составлении алгоритмов решения задач.

В вещественной компьютерной арифметике с ограниченным числом разрядов 1 + ε = 1 при 0 -n , где n — количество разрядов, отводимых для представления мантиссы вещественного числа.

При умножении двух целых чисел с плавающей запятой их порядки необходимо просто сложить, а мантиссы — перемножить (предварительное выравнивание не производится). При делении из порядка делимого надо вычесть порядок делителя, а мантиссу делимого разделить на мантиссу делителя.

Результатами выполнения операций умножения и деления нормализованных чисел а и b в арифметике с ограниченным числом разрядов будут:

Пример 13. Выполним умножение двух вещественных чисел:

0,23000 х 10 3 и 0,95000 х 10 7 .

При умножении двух вещественных чисел в представлении с плавающей запятой порядки складываются, а мантиссы перемножаются. В результате получим: 0,21850 х 10 10 . Это число не умещается в отведенный формат — в нашем формате под порядок отводится один разряд, а в получившемся числе порядок содержит две цифры. Выполнение операции умножения над этими числами приведет к прекращению выполнения программы в связи с ошибкой «переполнение порядка».

Пример 14. Выполним деление двух вещественных чисел: 0,92000 х 10 4 и 0,30000 х 10 7 . При делении вещественных чисел в представлении с плавающей запятой порядки вычитаются, а мантиссы делятся одна на другую. В нашем примере при делении мантисс мы имеем бесконечную периодическую дробь 0,92:0,3 = 3,0(6). Следовательно, при записи мантиссы результата произойдет ее округление. После нормализации результат будет иметь вид: 0,30667 х 10 -2 .

Источник