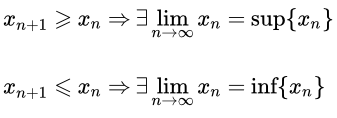Что значит невозрастающий порядок

Содержание

Монотонные последовательности
Что значит невозрастающий порядок
Теорема Вейерштрасса о пределе монотонной последовательности
Теорема Вейерштрасса о пределе монотонной последовательности
Доказательство
Пример решения задачи
невозрастающая последовательность
Тематики
Смотреть что такое «невозрастающая последовательность» в других словарях:
невозрастающая последовательность
Тематики
Смотреть что такое «невозрастающая последовательность» в других словарях:

Монотонные последовательности

Определение 35. Последовательность 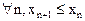n> называется невозрастающей, если .

Пример 25. 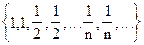— невозрастающая последовательность.

Определение 36. Последовательность 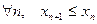n> называется неубывающей, если .

Пример 26. 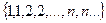неубывающая последовательность.

Определение 37. Последовательность 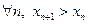n> называется возрастающей, если .

Пример 27. n> = < 1, 2, 3, 4, . >— возрастающая последовательность.

Определение 38. Последовательность 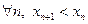n> называется убывающей, если .

Пример 28. 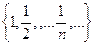n> = .

Невозрастающие, неубывающие, возрастающие, убывающие

последовательности называются монотонными последовательностями.

Замечание. Из определения возрастающей последовательности следует, что для установления возрастания последовательности с положительными членами достаточно установить неравенство .

Замечание. Из существования предела суммы, разности и предела произведения частного не следует существование предела каждой из последовательностей. Легко видеть

Пример 29. n> = (-1) n , n> = (-1) n +1 . Тогда

= 0, а . Хотя ни x_n, ни у_n предела не имеют.

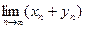
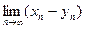
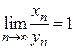
Пример 29. n> = n, n> = n, =0, .

Хотя x_n, у_n пределов не имеют.

Теорема 8. (о существовании предела монотонной ограниченной последовательности).

Пусть 1) n> — монотонно-возрастающая (убывающая),

Тогда 1),2)Þ 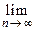x_n=а.

Доказательство. 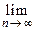n> — ограничена Þ то имеет точную верхнюю грань. Пусть supn> = a. Покажем, что x_n = а. По определению точной верхней грани для любого e>0 на множестве

Источник

Что значит невозрастающий порядок

Продолжаю цикл разбора алгоритмов по курсу, который я проходил на stepic.org. Сегодня рассмотрим достаточно сложную задачу.

Дано целое число $%1 \le n \le 10^5$% и массив $%A[1. n]$%, содержащий неотрицательные целые числа, не превосходящие $%10^9$%. Найдите наибольшую невозрастающую подпоследовательность в $%A$%. В первой строке выведите её длину $%k$%, во второй — её индексы $%1\le i_1 \lt i_2\lt \ldots \lt i_k \le n$% (таким образом, $%A[i_1] \ge A[i_2] \ge \ldots \ge A[i_n]$%)

Решение этой задачи методом динамического программирования со временем исполнения $%O(n^2)$% я написал достаточно быстро, и алгоритм решения на Python выглядит так:

Однако это решение не удалось сдать, т.к. при числах, приближающимся к $%10^9$% алгоритм начинал работать непозволительно долго. Требовалось найти решение, которое работает быстрее.

Пришлось немного погуглить и решение с временем работы — $%O(n log n)$% нашлось. Для решения моей задачи алгоритм из статьи понадобилось немного модифицировать.
Я сделал реверс заданной последовательности, а также добавил увеличение значения минимума при $%x[M[mid]] = x[i]$%.

Вот такой пример решения на Python у меня получился:

Наверно можно оптимизировать это решение, не выполняя реверс, но кажется от этого алгоритм потеряет наглядность, так как нужно будет выполнять обратный цикл и сравнивать элементы немного иначе.

Источник

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность < x_n > имеет конечный предел, равный точной верней границе, sup < x_n > для неубывающей и точной нижней границе, inf < x_n > для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность неубывающая, то для всех n выполняются неравенства:
(1.1) .

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
.
Это означает, что:

для всех n ,
(1.2) ;
для любого положительного числа , существует такой номер , зависящий от ε , так что
(1.3) .

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (1.3). Комбинируя с (1.2), находим:
при .
Поскольку , то
,
или
при .
Это и означает, что число является пределом последовательности .
Первая часть теоремы доказана.

2) Пусть теперь последовательность является невозрастающей ограниченной последовательностью:
(2.1) для всех n .

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
.
Это означает следующее:

для всех n выполняются неравенства:
(2.2) ;
для любого положительного числа , существует такой номер , зависящий от ε , для которого
(2.3) .

Поскольку последовательность невозрастающая, то при имеем:
.
Здесь мы также использовали (2.3). Учитывая (2.2), находим:
при .
Поскольку , то
,
или
при .
Это и означает, что число является пределом последовательности .
Вторая часть теоремы доказана.

Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то для всех n выполняются неравенства:
(3.1) .

Поскольку последовательность является неубывающей и неограниченной, то она неограниченна с правой стороны. Тогда для любого числа M существует такой номер , зависящий от M , для которого
(3.2) .

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (3.2).

Итак, для любого числа M существует такое натуральное число , зависящее от M , так что для всех номеров выполняются неравенства:
.
Это означает, что предел последовательности равен плюс бесконечности:
.
Третья часть теоремы доказана.

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Аналогично предыдущему, поскольку последовательность невозрастающая, то
(4.1) для всех n .

Поскольку последовательность является невозрастающей и неограниченной, то она неограниченна с левой стороны. Тогда для любого числа M существует такой номер , зависящий от M , для которого
(4.2) .

Поскольку последовательность невозрастающая, то при имеем:
.

Итак, для любого числа M существует такое натуральное число , зависящее от M , так что для всех номеров выполняются неравенства:
.
Это означает, что предел последовательности равен минус бесконечности:
.
Теорема доказана.

Пример решения задачи

Все примеры Пользуясь теоремой Вейерштрасса, доказать сходимость последовательности:
, , . . . , , . . .
После чего найти ее предел.

Представим последовательность в виде рекуррентных формул:
,
.

Докажем, что заданная последовательность ограничена сверху значением
(П1) .
Доказательство выполняем методом математической индукции.
.
Пусть . Тогда
.
Неравенство (П1) доказано.

Докажем, что последовательность монотонно возрастает.
;
(П2) .
Поскольку , то знаменатель дроби и первый множитель в числителе положительные. В силу ограниченности членов последовательности неравенством (П1), второй множитель также положителен. Поэтому
.
То есть последовательность является строго возрастающей.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Найдем этот предел. Обозначим его через a :
.
Воспользуемся тем, что
.
Применим это к (П2), используя арифметические свойства пределов сходящихся последовательностей:
.
Условию удовлетворяет корень .

Автор: Олег Одинцов . Опубликовано: 25-09-2017

Источник

невозрастающая последовательность

невозрастающая последовательность
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]

Тематики

информационные технологии в целом

Справочник технического переводчика. – Интент . 2009-2013 .

Смотреть что такое «невозрастающая последовательность» в других словарях:

Невозрастающая функция — Монотонная функция это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Содержание 1 Определения 2… … Википедия

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств.… … Википедия

Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия

Монотонность последовательности — Монотонная последовательность последовательность , удовлетворяющая одному из следующих условий: для любого номера выполняется неравенство (неубывающая последовательность), для любого номера выполняется неравенство (невозрастающая… … Википедия

Степень вершины (теория графов) — Рис. 1. Граф, на вершинах которого отмечены степени. Степень вершины (англ. degree, также валент … Википедия

ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ — функция из первого Бэра класса. Подробнее, числовая функция f, определенная на полном метрич. пространстве X, наз. полунепрерывной снизу (сверху) в точке , если Функция f наз. полунепрерывной снизу (сверху) на X, если она. полунепрерывна снизу… … Математическая энциклопедия

ТРАНСФИНИТНЫЙ ДИАМЕТР — компактного множества характеристика d=d(E)компактного множества Ена комплексной плоскости, служащая геометрии, интерпретацией емкости этого множества. Пусть Е компактное бесконечное множество плоскости z. Величина где [ а, b]=|а b| евклидово… … Математическая энциклопедия

МЕТРИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются и метрически (т. е. на основе теории меры )характеризуются множества чисел, обладающих определенными арифметич. свойствами. М. т. ч. тесно связана с теорией вероятностей, что иногда дает возможность… … Математическая энциклопедия

Карацуба — Карацуба, Анатолий Алексеевич Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937(1937 01 31) … Википедия

Карацуба, Анатолий Алексеевич — Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937 … Википедия

Источник

невозрастающая последовательность

Тематики

информационные технологии в целом

Русско-английский словарь нормативно-технической терминологии . academic.ru . 2015 .

Смотреть что такое «невозрастающая последовательность» в других словарях:

невозрастающая последовательность — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN non increasing sequence … Справочник технического переводчика

Карацуба, Анатолий Алексеевич — Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937 … Википедия

Источник