Что значит непрерывная функция пример

Непрерывность функции в точке и на промежутке. С примерами

Примеры и условия непрерывности функции. Непрерывность в точке и на промежутке

На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на то что записываются как 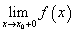и .

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Графически функция непрерывна в точке , если её график не «разрывается» в этой точке. График такой непрерывной функции — показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

1. Функция определена в точке .

2. Существует предел функции в точке , при этом правый и левый пределы равны: . Правый и левый пределы вычисляются как предел вообще: в выражение функции вместо икса подставляется то, к чему стремится икс, причём вместе с плюс нулём при правом пределе и с минус нулём при левом пределе.

3. Предел функции в точке равен значению функции в этой точке:

А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому стремится икс, прибавляется или вычитается всего лишь нуль? Могут. Когда и почему — это объяснено на уроке о точках разрыва функции и их видах.

Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 — на рисунке ниже.

Пример 1. Функция f(x) определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0 , x = 1 , x = 3 ?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0 . Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

.

Предел функции и значение функции в точке x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0 .

Точка x = 1 . Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1 .

Точка x = 3 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3 .

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение

Пример 2. Установить, непрерывна ли функция в точке x = 2 .

Пример 3. Установить, непрерывна ли функция в точке x = 8 .

Что такое непрерывное изменение функции?

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m , то есть l = f(m) , m≥0 .

Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l . Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f(m) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f(m) непрерывна, а в точке она имеет разрыв.

Если речь идёт о косвенном измерении y путём измерения величины x , то слова «при малом изменении x величина y меняется мало», означают: «при малой ошибке в измерении x погрешность значения y мала». Точнее говоря, погрешность значения y можно сделать сколь угодно малой, если достаточно точно измерить значение x .

Величина погрешности измерения оценивается наибольшей допустимой ошибкой или, иначе говоря, точностью измерения. Если величина x измерена с точностью , то это означает, что отклонение полученного значения x от точного значения a меньше , то есть что . Таким образом, какая бы точность ни была задана, всегда можно добиться того, чтобы отклонение f(x) от f(a) было меньше, то есть . Добиться такой точности можно, выбрав x достаточно близким к a .

Из неравенства следует неравенство .

Вернёмся к примеру с висящим грузом. Для любого заранее указанного удлинения нити можно подобрать такое значение , что если масса дополнительной нагрузки меньше , то нить удлинится менее чем на .

Определение непрерывности функции через окрестность точки. Функция является непрерывной в точке a при соблюдении двух условий:

1) функция определена в некоторой окрестности точки a ;

2) для любого существует такое , что из следует (если отклонение x от a ) меньше , то отклонение f(x) от f(a) меньше .

Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика.

Непрерывность функции на промежутке

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a, b] , функция непрерывна на отрезке [0, b] , функция непрерывна на любом отрезке, не содержащем точку a = 2 .

Пример 4. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках — 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

.

Найдём правосторонний предел при :

.

Очевидно, что значение в точке x = 2 должно быть равно ax :

Ответ: функция непрерывна на всей области определения при a = 1,5 .

Пример 6. Определить, при каких значениях параметров a и b непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

.

Следовательно, значение в точке должно быть равно 1:

.

Найдём левосторонний функции в точке :

.

Очевидно, что значение функции в точке должно быть равно :

Ответ: функция непрерывна на всей области определения при a = 1; b = -3 .

Основные свойства непрерывных функций

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t , выраженная законом s = f(t) , даёт пример непрерывной функции f(t) . Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t) .

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f(x) , непрерывная на интервале [a, b] , принимает все промежуточные значения между значениями в концевых точках, то есть, между f(a) и f(b) . В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

3. Если функция непрерывна на интервале, то на этом интервале она достигает своего наибольшего и своего наименьшего значения: если m — наименьшее, а M — наибольшее значение функции на интервале [a, b] , то найдутся на этом отрезке такие точки и , что и . Теорема, в которой изложено это свойство, называется второй теоремой Вейерштрасса.

Пример 7. Используя первое из приведённых выше свойств непрерывных функций, доказать, что уравнение имеет по меньшей мере один вещественный корень в интервале [1; 2] .

Пусть .

Вычислим значения функции при x = 1 и x = 2 .

.

.

Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.

Следовательно, в интервале [1; 2] существует такое число a , при котором f(a) = 0 . То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.

Установление непрерывности функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.

Пример 8. Есть ли у уравнения хотя бы один вещественный корень?

Решение.
Функция определена на интервале .

Вычислим значения функции при x = 0 и .

.

.

Получили
и .

Следовательно, существует такое число a , при котором f(a) = 0 . Ответ на вопрос задачи: уравнение имеет по меньшей мере один вещественный корень.

Источник